
题目列表(包括答案和解析)
17. 已知椭圆 ,它的上下顶点分别是A、B,点M是椭圆上的动点(不与A、B重合),直线AM交直线
,它的上下顶点分别是A、B,点M是椭圆上的动点(不与A、B重合),直线AM交直线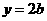 于点N,且
于点N,且 .(1)求椭圆的离心率;(2)若斜率为1的直线l交椭圆于P、Q两点,求证:
.(1)求椭圆的离心率;(2)若斜率为1的直线l交椭圆于P、Q两点,求证: 与向量
与向量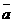 =(-3,1)共线(其中O为坐标原点)
=(-3,1)共线(其中O为坐标原点)
解:(1)设M(x0,y0),又点A(0,b),B(0,-b) ∴直线AM:





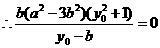
解得: ,即离心率
,即离心率 .
.
(2)设直线l:

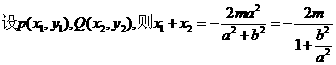

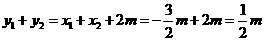


16.已知 为椭圆E的两个左右焦点,抛物线C以
为椭圆E的两个左右焦点,抛物线C以 为顶点,
为顶点, 为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足
为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足 ,则e的值为
,则e的值为
|
14.双曲线 的两条渐近线互相垂直,那么该双曲线的离心率是
的两条渐近线互相垂直,那么该双曲线的离心率是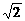
15 过双曲线M: 的左顶点A作斜率为1的直线
的左顶点A作斜率为1的直线 ,若
,若 与双曲线M的两条渐近线分别相交于B、C,且|AB|=|BC|,则双曲线M的离心率是
与双曲线M的两条渐近线分别相交于B、C,且|AB|=|BC|,则双曲线M的离心率是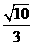
13. 如图所示,B(– c,0),C(c,0),AH⊥BC,垂足为H,且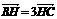 .
.
(1)若 =
0,求以B、C为焦点并且经过点A的椭圆的离心率;
=
0,求以B、C为焦点并且经过点A的椭圆的离心率;
(2)D分有向线段 的比为
的比为 ,A、D同在以B、C为焦点的椭圆上,
,A、D同在以B、C为焦点的椭圆上,
当 ―5≤ ≤
≤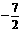 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.
.解:(1)因为 ,所以H
,所以H ,又因为AH⊥BC,所以设A
,又因为AH⊥BC,所以设A ,由
,由 得
得 即
即 3分
3分
所以|AB| = ,|AC | =
,|AC | =
椭圆长轴2a = |AB| + |AC| = ( +
1)c, 所以,
+
1)c, 所以, .
.
(2)设D (x1,y1),因为D分有向线段 的比为,所以
的比为,所以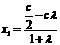 ,
, ,
,
设椭圆方程为 =
1 (a > b > 0),将A、D点坐标代入椭圆方程得
=
1 (a > b > 0),将A、D点坐标代入椭圆方程得  .①
.①
 …………………………….. ②
…………………………….. ②
由①得
 ,代入②并整理得
,代入②并整理得 ,
,
因为 – 5≤≤ ,所以
,所以 ,又0 < e < 1,所以
,又0 < e < 1,所以 ≤e≤
≤e≤ .
.
10. 如图,椭圆的中心在原点,长轴AA1在x轴上.以A、A1为焦点的双曲线交椭圆于C、D、D1、C1四点,且|CD|= |AA1|.椭圆的一条弦AC交双曲线于E,设
|AA1|.椭圆的一条弦AC交双曲线于E,设 ,当
,当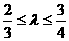 时,求双曲线的离心率e的取值范围.
时,求双曲线的离心率e的取值范围.
解:设A(-c,0),A1(c,0),则 (其中c为双曲线的半焦距,h为C、D到x轴的距离)
(其中c为双曲线的半焦距,h为C、D到x轴的距离)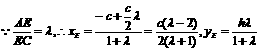 即E点坐标为
即E点坐标为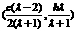
设双曲线的方程为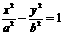 ,将
,将 代入方程,得
代入方程,得 ①
①
将 代入①式,整理得
代入①式,整理得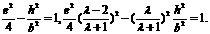
消去
由于
11 若F 、F
、F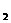 为双曲线
为双曲线 的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足;
的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足;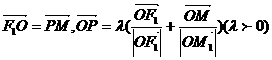 .(1)求该双曲线的离心率;(2)若该双曲线过N(2,
.(1)求该双曲线的离心率;(2)若该双曲线过N(2, ),求双曲线的方程;(3)若过N(2,
),求双曲线的方程;(3)若过N(2, )的双曲线的虚轴端点分别为B
)的双曲线的虚轴端点分别为B 、B
、B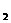 (B
(B 在y轴正半轴上),点A
在y轴正半轴上),点A
.解:(1)由 知四边形PF
知四边形PF 为平行四边形,∵
为平行四边形,∵
( ∴OP平分∠
∴OP平分∠ ,∴平行四边形PFOM 为菱形,又∵
,∴平行四边形PFOM 为菱形,又∵
∴
 .
.
(2)∵ ∴
∴ ∴双曲线的方程为
∴双曲线的方程为 ∴所求双曲线的方程为
∴所求双曲线的方程为
(3)依题意得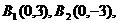 ∴
∴ 、B
、B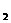 、B共线,不妨设直线AB为:
、B共线,不妨设直线AB为:
y=kx-3,A(x 则有
则有 ,得
,得 ,因为
,因为 的渐进线为
的渐进线为 ,当
,当 时,AB与双曲线只有一个交点,不合题意,当
时,AB与双曲线只有一个交点,不合题意,当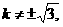 ∴
∴ ,
,
又 ,∴
,∴ ∴所求的直线AB的方程为
∴所求的直线AB的方程为 .
.
12 已知双曲线
 (a>0,b>0)的右准线
(a>0,b>0)的右准线 一条渐近线
一条渐近线 交于两点P、Q,F是双曲线的右焦点。(I)求证:PF⊥
交于两点P、Q,F是双曲线的右焦点。(I)求证:PF⊥ ;(II)若△PQF为等边三角形,且直线y=x+b交双曲线于A,B两点,且
;(II)若△PQF为等边三角形,且直线y=x+b交双曲线于A,B两点,且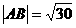 ,求双曲线的方程;(III)延长FP交双曲线左准线
,求双曲线的方程;(III)延长FP交双曲线左准线 和左支分别为点M、N,若M为PN的中点,求双曲线的离心率e。
和左支分别为点M、N,若M为PN的中点,求双曲线的离心率e。
.解:(1) 不妨设 .
.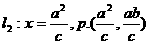 ,
F.(c,0)
,
F.(c,0)
设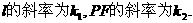 k2=
k2= ∴k1k2=-1.
∴k1k2=-1.
即PF⊥ . (2)由题
. (2)由题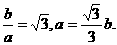
 . x2-bx-b2=0,
. x2-bx-b2=0, 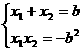

∴a=1, ∴双曲线方程为
(3) y=-
y=- M(-
M(-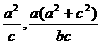
 ∴N(-
∴N(- ).
).
又N在双曲线上。∴ ∴e=
∴e=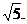
9. 椭圆的中心在坐标原点O,右焦点F(c,0)到相应准线的距离为1,倾斜角为45°的直线交椭圆于A,B两点.设AB中点为M,直线AB与OM的夹角为 a(1)用半焦距c表示椭圆的方程及tg
a(1)用半焦距c表示椭圆的方程及tg ;(2)若2<tg
;(2)若2<tg <3,求椭圆率心率e的取值范围.
<3,求椭圆率心率e的取值范围.
.解:(1)由题意可知 所以椭圆方程为
所以椭圆方程为
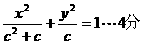 设
设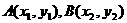 ,将其代入椭圆方程相减,将
,将其代入椭圆方程相减,将
 代入 可化得
代入 可化得 
(2)若2<tg <3,则
<3,则
3.已知 是双曲线的两个焦点,
是双曲线的两个焦点,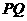 是经过
是经过 且垂直于实轴的弦,若
且垂直于实轴的弦,若 是等腰直角三角形,则双曲线的离心率为
是等腰直角三角形,则双曲线的离心率为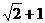
4已知双曲线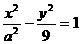
 的中心在原点, 右焦点与抛物线
的中心在原点, 右焦点与抛物线 的焦点重合,则该双曲线的离心率等于
的焦点重合,则该双曲线的离心率等于
5设双曲线C: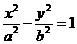 (a>0,b>0)的离心率为e,若准线l与两条渐近线相交于P、Q两点,F为右焦点,△FPQ为等边三角形.(1)求双曲线C的离心率e的值;
(a>0,b>0)的离心率为e,若准线l与两条渐近线相交于P、Q两点,F为右焦点,△FPQ为等边三角形.(1)求双曲线C的离心率e的值;
 解:右准线l的方程为:x=
解:右准线l的方程为:x= ,两条渐近线方程为:
,两条渐近线方程为: .
.
∴ 两交点坐标为 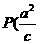 ,
, 、
、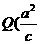 ,
, .
.
∵ △PFQ为等边三角形,则有 (如图).
(如图).
∴ 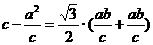 ,即
,即 .
.
解得  ,c=2a.∴
,c=2a.∴ 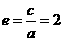 .
.
6椭圆 (a>b>0)离心率为
(a>b>0)离心率为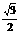 ,则双曲线
,则双曲线 的离心率为
的离心率为 
7 设双曲线 (0<a<b)的半焦距c, 直线l过(a, 0), (0, b)两点. 已知原点到直线l的距离为
(0<a<b)的半焦距c, 直线l过(a, 0), (0, b)两点. 已知原点到直线l的距离为 c,
则双曲线的离心率为
[解析]:直线l过(a, 0), (0, b)两点. 即为:
c,
则双曲线的离心率为
[解析]:直线l过(a, 0), (0, b)两点. 即为: ,故原点到直线l的距离
,故原点到直线l的距离 =
= c,
c, ∴e =
∴e =  或2,又0<a<b,∴e = 2
或2,又0<a<b,∴e = 2
8 点P(-3,1)在椭圆 的左准线上,过点P且方向为
的左准线上,过点P且方向为 的光线,经直线
的光线,经直线 反射后通过椭圆的左焦点,则这个椭圆的离心率为 [解析]: 点P(-3,1)在椭圆
反射后通过椭圆的左焦点,则这个椭圆的离心率为 [解析]: 点P(-3,1)在椭圆 的左准线上, 故点P(-3,1)关于直线
的左准线上, 故点P(-3,1)关于直线 的对称的点为Q,则Q(-3,-5),设椭圆的左焦点为F,则直线FQ为
的对称的点为Q,则Q(-3,-5),设椭圆的左焦点为F,则直线FQ为 ,故
,故 ∴
∴ 1,
1,
6. 如图,在底面为直角梯形的四棱锥
如图,在底面为直角梯形的四棱锥

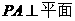 ABCD,
ABCD, ,BC=6.
,BC=6.
(Ⅰ)求证: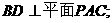
(Ⅱ)求二面角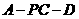 的平面角的余弦值.
的平面角的余弦值.
解:(Ⅰ)如图,建立坐标系,则 ,
,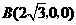 ,
, ,
,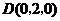 ,
, ,
,
 ,
, ,
, ,
,
 ,
, .
. ,
, ,
,
又 ,
, 平面
平面 .
.
(Ⅱ)设平面 的法向量为
的法向量为 ,则
,则 ,
, ,
,
又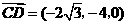 ,
, ,
, 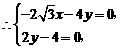 解得
解得
 平面
平面 的法向量取为
的法向量取为 ,
,
设二面角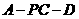 的平面角为
的平面角为 ,
, 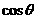
 .
.
5.解:(1)由折起的过程可知,PE⊥平面ABC, ,
,
V(x)= (
(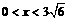 )
)
(2) ,所以
,所以 时,
时,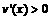 ,V(x)单调递增;
,V(x)单调递增; 时
时 ,V(x)单调递减;因此x=6时,V(x)取得最大值
,V(x)单调递减;因此x=6时,V(x)取得最大值 ;
;
(3)过F作MF//AC交AD与M,则 ,PM=
,PM=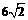 ,
,
 ,
,
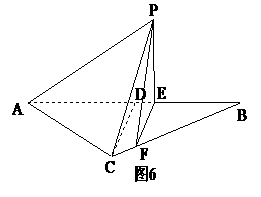
5.如图6所示,等腰三角形△ABC的底边AB=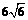 ,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积。
,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积。
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com