
题目列表(包括答案和解析)
9、(2009湛江一模)已知函数 .(
.(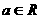 )
)
(Ⅰ)当 时,求
时,求 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数 的图象恒在直线
的图象恒在直线 下方,求
下方,求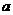 的取值范围.
的取值范围.
解:(Ⅰ)当 时,
时, ,
,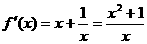 ;………………2分
;………………2分
对于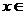 [1,e],有
[1,e],有 ,∴
,∴ 在区间[1,e]上为增函数,…………3分
在区间[1,e]上为增函数,…………3分
∴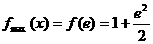 ,
,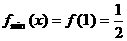 .……………………………5分
.……………………………5分
(Ⅱ)令 ,则
,则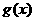 的定义域为(0,+∞).
的定义域为(0,+∞).
……………………………………………6分
在区间(1,+∞)上,函数 的图象恒在直线
的图象恒在直线 下方等价于
下方等价于 在区间(1,+∞)上恒成立.
在区间(1,+∞)上恒成立.
∵
① 若 ,令
,令 ,得极值点
,得极值点 ,
,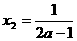 ,………………8分
,………………8分
当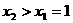 ,即
,即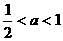 时,在(
时,在( ,+∞)上有
,+∞)上有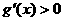 ,
,
此时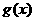 在区间(
在区间( ,+∞)上是增函数,并且在该区间上有
,+∞)上是增函数,并且在该区间上有
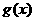 ∈(
∈( ,+∞),不合题意;………………………………………9分
,+∞),不合题意;………………………………………9分
当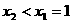 ,即
,即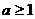 时,同理可知,
时,同理可知,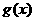 在区间(1,+∞)上,有
在区间(1,+∞)上,有
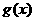 ∈(
∈( ,+∞),也不合题意;………………………………………10分
,+∞),也不合题意;………………………………………10分
② 若 ,则有
,则有 ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有 ,
,
从而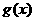 在区间(1,+∞)上是减函数;……………………………………12分
在区间(1,+∞)上是减函数;……………………………………12分
要使 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足
 ,
,
由此求得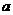 的范围是[
的范围是[ ,
,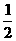 ].
].
综合①②可知,当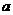 ∈[
∈[ ,
,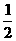 ]时,函数
]时,函数 的图象恒在直线
的图象恒在直线 下方.
下方.
………………………………………………14分
2009年联考题
8、(2009深圳一模)已知函数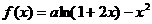 (
( ,
, ).
).
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若不等式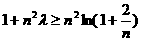 对一切正整数
对一切正整数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
解:(Ⅰ) ………………… 2分
………………… 2分
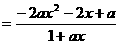 ,
,
由 ,得
,得 .
.
 ,
,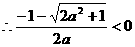 ,
,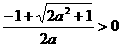 .
.
又 .
.
 函数
函数 的单调递增区间为
的单调递增区间为 ,递减区间为
,递减区间为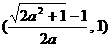 . ………… 6分
. ………… 6分
(Ⅱ)[法一]不等式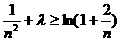 ,即为
,即为 .……………(※)
.……………(※)
令 ,当
,当 时,
时, .
.
则不等式(※)即为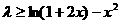 .
…………………9分
.
…………………9分
令 ,
, ,
,
 在
在 的表达式中,当
的表达式中,当 时,
时,
 ,
,
又
 时,
时,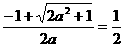 ,
,

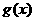 在
在 单调递增,在
单调递增,在 单调递减.
单调递减.
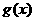 在
在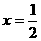 时,取得最大,最大值为
时,取得最大,最大值为 . …………………12分
. …………………12分
因此,对一切正整数 ,当
,当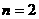 时,
时, 取得最大值
取得最大值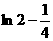 .
.
 实数
实数 的取值范围是
的取值范围是 . ………………………… 14分
. ………………………… 14分
[法二]不等式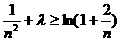 ,即为
,即为 .………………(※)
.………………(※)
设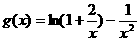
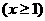 ,
,
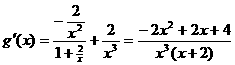 ,
,
令 ,得
,得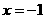 或
或 .
………………………… 10分
.
………………………… 10分
 当
当 时,
时,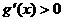 ,当
,当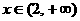 时,
时, .
.
 当
当 时,
时,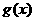 取得最大值
取得最大值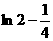 .
.
因此,实数 的取值范围是
的取值范围是 .
………………………… 14分
.
………………………… 14分
7、
解: (1)  ,两边加
,两边加 得:
得:  ,
,
 是以2为公比,
是以2为公比, 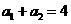 为首项的等比数列.
为首项的等比数列.  ……①
……①
由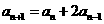 两边减
两边减 得:
得: 
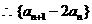 是以
是以
为公比, 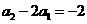 为首项的等比数列.
为首项的等比数列.  ……②
……②
①-②得: 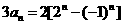 所以,所求通项为
所以,所求通项为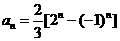 …………5分
…………5分
(2) 当 为偶数时,
为偶数时,
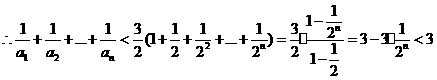
当 为奇数时,
为奇数时,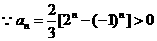 ,
, ,又
,又 为偶数
为偶数
 由(1)知,
由(1)知,  ……………………10分
……………………10分
(3)证明: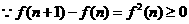

又
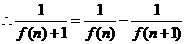 ……12分
……12分
 …………14分
…………14分
6、(2009昆明一中第三次模拟)已知
(1) 若函数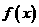 是
是 上的增函数,求
上的增函数,求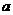 的取值范围;
的取值范围;
(2) 若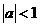 ,求
,求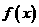 的单调增区间
的单调增区间
解:(Ⅰ) ,
,
 是
是 上的增函数,故
上的增函数,故 在
在 上恒成立,
上恒成立,
即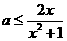 在
在 上恒成立
上恒成立
 的最小值为
的最小值为 ,故知a的取值范围是
,故知a的取值范围是
(2)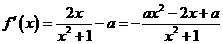 由
由 ,得
,得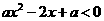 ,
,
①当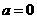 时,
时, ,即函数
,即函数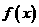 在
在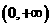 上单调递增;
上单调递增;
 时,由判别式
时,由判别式 可知
可知
②当 时,有
时,有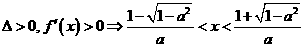 ,
,
即函数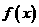 在
在 上单调递增;
上单调递增;
③当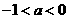 时,有
时,有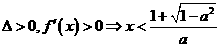 或
或 ,
,
即函数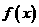 在
在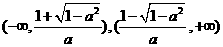 上单调递增
上单调递增
5、(2009茂名一模)已知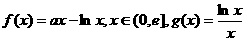 ,其中
,其中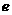 是自然常数,
是自然常数,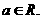
(Ⅰ)讨论 时,
时,  的单调性、极值;
的单调性、极值;
(Ⅱ)求证:在(Ⅰ)的条件下, ;
;
(Ⅲ)是否存在实数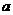 ,使
,使 的最小值是3,若存在,求出
的最小值是3,若存在,求出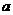 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅰ)
 ,
, ……1分
……1分
∴当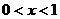 时,
时,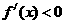 ,此时
,此时 单调递减
单调递减
当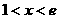 时,
时,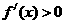 ,此时
,此时 单调递增 ……3分
∴
单调递增 ……3分
∴ 的极小值为
的极小值为 ……4分
……4分
(Ⅱ)
 的极小值为1,即
的极小值为1,即 在
在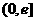 上的最小值为1, ∴
上的最小值为1, ∴ 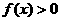 ,
, ……5分
……5分
令 ,
, , ……6分
, ……6分
当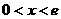 时,
时, ,
, 在
在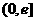 上单调递增 ……7分
上单调递增 ……7分
∴ ∴在(1)的条件下,
∴在(1)的条件下, ……9分
……9分
(Ⅲ)假设存在实数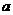 ,使
,使 (
( )有最小值3,
)有最小值3,
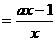 …9分
…9分
①
当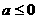 时,
时, 在
在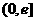 上单调递减,
上单调递减,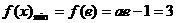 ,
, (舍去),所以,
(舍去),所以,
此时 无最小值. ……10分 ②当
无最小值. ……10分 ②当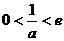 时,
时, 在
在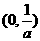 上单调递减,在
上单调递减,在 上单调递增
上单调递增
 ,
,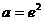 ,满足条件. ……11分
,满足条件. ……11分
③
当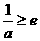 时,
时, 在
在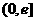 上单调递减,
上单调递减,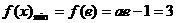 ,
, (舍去),所以,此时
(舍去),所以,此时 无最小值.综上,存在实数
无最小值.综上,存在实数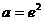 ,使得当
,使得当 时
时 有最小值3.
有最小值3.
4、(2009东莞一模)已知 ,
, ,
,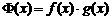 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)求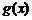 在点
在点 处的切线与直线
处的切线与直线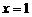 及曲线
及曲线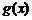 所围成的封闭图形的面积;
所围成的封闭图形的面积;
(3)是否存在实数 ,使
,使 的极大值为3?若存在,求出
的极大值为3?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
解:(1)当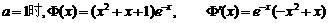 .…(1分)
.…(1分)
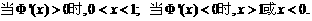 ……(3分)
……(3分)
∴ 的单调递增区间为(0,1),单调递减区间为:
的单调递增区间为(0,1),单调递减区间为: ,
,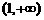 .
.
……(4分)
(2)切线的斜率为 ,
,
∴ 切线方程为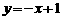 .……(6分)
.……(6分)
所求封闭图形面积为
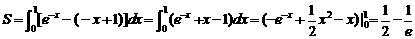 .
.
……(8分)
(3) , ……(9分)
, ……(9分)
令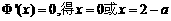 .
……(10分)
.
……(10分)
列表如下:
|
x |
(-∞,0) |
0 |
(0,2-a) |
2-a |
(2-a,+ ∞) |
 |
- |
0 |
+ |
0 |
- |
 |
↘ |
极小 |
↗ |
极大 |
↘ |
由表可知,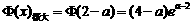 .
……(12分)
.
……(12分)
设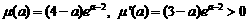 ,
,
∴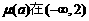 上是增函数,……(13分)
上是增函数,……(13分)
∴  ,即
,即 ,
,
∴不存在实数a,使 极大值为3.
……(14)
极大值为3.
……(14)
3、(2009临沂一模)设函数f(x)=x2-mlnx,h(x)=x2-x+a.
(I) 当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,求实数m的取值范围;
(II) 当m=2时,若函数k(x)=f(x)-h(x)在[1,3]上恰有两个不同零点,求实数 a的取值范围;
(III) 是否存在实数m,使函数f(x)和函数h(x)在公共定义域上具有相同的单调性?若存在,求出m的值,若不存在,说明理由。
解:(1)由a=0,f(x)≥h(x)可得-mlnx≥-x 即
记 ,则f(x)≥h(x)在(1,+∞)上恒成立等价于
,则f(x)≥h(x)在(1,+∞)上恒成立等价于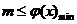 .
.
求得
当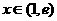 时;
时; ;当
;当 时,
时,
故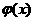 在x=e处取得极小值,也是最小值,
在x=e处取得极小值,也是最小值,
即 ,故
,故 .
.
(2)函数k(x)=f(x)-h(x)在[1,3]上恰有两个不同的零点等价于方程x-2lnx=a,在[1,3]上恰有两个相异实根。
令g(x)=x-2lnx,则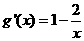
当 时,
时, ,当
,当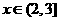 时,
时,
g(x)在[1,2]上是单调递减函数,在 上是单调递增函数。
上是单调递增函数。
故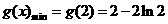 又g(1)=1,g(3)=3-2ln3
又g(1)=1,g(3)=3-2ln3
∵g(1)>g(3),∴只需g(2)<a≤g(3),
故a的取值范围是(2-2ln2,3-2ln3)
(3)存在m=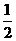 ,使得函数f(x)和函数h(x)在公共定义域上具有相同的单调性
,使得函数f(x)和函数h(x)在公共定义域上具有相同的单调性
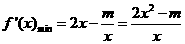 ,函数f(x)的定义域为(0,+∞)。
,函数f(x)的定义域为(0,+∞)。
若 ,则
,则 ,函数f(x)在(0,+∞)上单调递增,不合题意;
,函数f(x)在(0,+∞)上单调递增,不合题意;
若 ,由
,由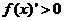 可得2x2-m>0,解得x>
可得2x2-m>0,解得x>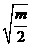 或x<-
或x<-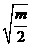 (舍去)
(舍去)
故 时,函数的单调递增区间为(
时,函数的单调递增区间为(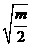 ,+∞)
,+∞)
单调递减区间为(0,
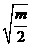 )而h(x)在(0,+∞)上的单调递减区间是(0,
)而h(x)在(0,+∞)上的单调递减区间是(0,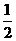 ),单调递增区间是(
),单调递增区间是(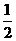 ,+∞)
,+∞)
故只需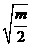 =
=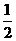 ,解之得m=
,解之得m=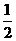 即当m=
即当m=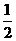 时,函数f(x)和函数h(x)在其公共定义域上具有相同的单调性。
时,函数f(x)和函数h(x)在其公共定义域上具有相同的单调性。
2、(2009昆明市期末)已知函数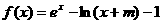 ,若x=0,函数f(x)取得极值
,若x=0,函数f(x)取得极值
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)已知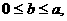 证明:
证明: .
.
解:(Ⅰ)
由 x=0是极值点,故 ,得
,得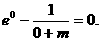
故 m=1.
故 
当 -1<x<0时, 函数在(-1,0)内是减函数;
函数在(-1,0)内是减函数;
当 x>0时,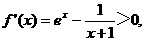 函数f(x)在(0,+∞)内是增函数。
函数f(x)在(0,+∞)内是增函数。
所以x=0时,f(0)=0,则函数f(x)取得最小值为0.·························6分
(Ⅱ)由(Ⅰ)知:f(x)≥0,故ex-1≥ln(x+1)。
∵ ①··············8分
①··············8分
又 
=
故  ················································10分
················································10分
故 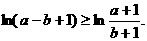 ②
②
由①②得 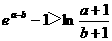 ···········································12分
···········································12分
1、(2009聊城一模)已知函数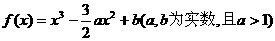 在区间[-1,1]上最大值为1,最小值为-2。
在区间[-1,1]上最大值为1,最小值为-2。
(1)求 的解析式;
的解析式;
(2)若函数 在区间[-2,2]上为减函数,求实数m的取值范围。
在区间[-2,2]上为减函数,求实数m的取值范围。
解:(1)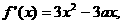


(2)
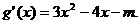
由 ,
,
知
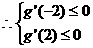 , 即
, 即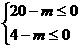
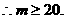
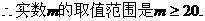
7.(2009宣威六中第一次月考)已知函数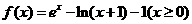 ,则函数f(x)的最小值是
,则函数f(x)的最小值是
答案 0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com