3.正六棱锥P-ABCDEF中，G为PB的中点，则三棱锥D-GAC与三棱锥P-GAC体积之比为

(A)1：1　　 (B) 1：2　　 (C) 2：1　　 (D) 3：2

2.一个棱锥的三视图如图，则该棱锥的全面积(单位：c)为

(A)48+12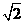　　　 (B)48+24　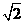　 (C)36+12　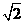 (D)36+24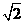

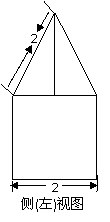
1. 一空间几何体的三视图如图所示,则该几何体的体积为(　　　　 ).

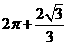A.　　　 B. 　　　　　　C. 　　　　　D.

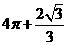
[解析]:该空间几何体为一圆柱和一四棱锥组成的,

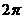圆柱的底面半径为1,高为2,体积为,四棱锥的底面

边长为，高为，

所以体积为

所以该几何体的体积为.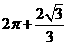

答案:C

[命题立意]:本题考查了立体几何中的空间想象能力,

由三视图能够想象得到空间的立体图,并能准确地

计算出.几何体的体积.

4.(2010四川理)(18)(本小题满分12分)

已知正方体ABCD－A'B'C'D'的棱长为1，点M是棱AA'的中点，点O是对角线BD'的中点.

(Ⅰ)求证：OM为异面直线AA'和BD'的公垂线；

(Ⅱ)求二面角M－BC'－B'的大小；

(Ⅲ)求三棱锥M－OBC的体积.

本小题主要考查异面直线、直线与平面垂直、二面角、正方体、三棱锥体积等基础知识，并考查空间想象能力和逻辑推理能力，考查应用向量知识解决数学问题的能力。

解法一：(1)连结AC，取AC中点K，则K为BD的中点，连结OK

因为M是棱AA’的中点，点O是BD’的中点

所以AM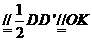

所以MO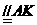

由AA’⊥AK，得MO⊥AA’

因为AK⊥BD,AK⊥BB’，所以AK⊥平面BDD’B’

所以AK⊥BD’

所以MO⊥BD’

又因为OM是异面直线AA’和BD’都相交

故OM为异面直线AA'和BD'的公垂线

(2)取BB’中点N，连结MN，则MN⊥平面BCC’B’

过点N作NH⊥BC’于H，连结MH

则由三垂线定理得BC’⊥MH

从而,∠MHN为二面角M-BC’-B’的平面角

MN=1,NH=Bnsin45°=

在Rt△MNH中，tan∠MHN=

故二面角M-BC’-B’的大小为arctan2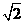

(3)易知，S_△OBC=S_△OA’D’，且△OBC和△OA’D’都在平面BCD’A’内

点O到平面MA’D’距离h＝

V_M-OBC=V_M-OA’D’=V_O-MA’D’=S_△MA’D’h=

解法二：

以点D为坐标原点，建立如图所示空间直角坐标系D-xyz

则A(1,0,0),B(1,1,0),C(0,1,0),A’(1,0,1),C’(0,1,1),D’(0,0,1)

(1)因为点M是棱AA’的中点,点O是BD’的中点

所以M(1,0, ),O(,,)

,=(0,0,1),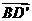=(-1,-1,1)

=0, +0=0

所以OM⊥AA’,OM⊥BD’

又因为OM与异面直线AA’和BD’都相交

故OM为异面直线AA'和BD'的公垂线.………………………………4分

(2)设平面BMC'的一个法向量为=(x,y,z)

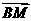=(0,-1,), ＝(－1,0,1)

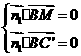　 即

取z＝2,则x＝2,y＝1，从而=(2,1,2)

取平面BC'B'的一个法向量为＝(0,1,0)

cos

由图可知，二面角M-BC'-B'的平面角为锐角

故二面角M-BC'-B'的大小为arccos………………………………………………9分

(3)易知，S_△OBC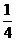＝S_△BCD'A'＝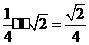

设平面OBC的一个法向量为＝(x₁,y₁,z₁)

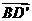＝(－1,－1,1), 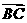＝(－1,0,0)

　 即

取z₁＝1,得y₁＝1，从而＝(0,1,1)

点M到平面OBC的距离d＝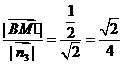

V_M－OBC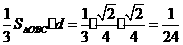＝…………………………………………12分

2009年高考题

3.(2010安徽文)19.(本小题满分13分)

如图，在多面体ABCDEF中，四边形ABCD是正方形，AB=2EF=2，EF∥AB,EF⊥FB,∠BFC=90°，BF=FC,H为BC的中点，

(Ⅰ)求证：FH∥平面EDB;

(Ⅱ)求证：AC⊥平面EDB;

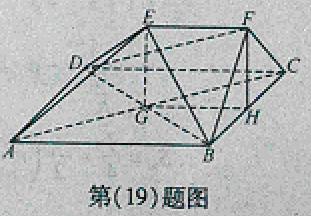(Ⅲ)求四面体B-DEF的体积；

[命题意图]本题考查空间线面平行、线面垂直、面面垂直的判断与证明，考查体积的计算等基础知识，同时考查空间想象能力、推理论证能力和运算能力.

[解题指导](1)设底面对角线交点为G，则可以通过证明EG∥FH，得∥平面；(2)利用线线、线面的平行与垂直关系，证明FH⊥平面ABCD，得FH⊥BC，FH⊥AC，进而得EG⊥AC，平面；(3)证明BF⊥平面CDEF，得BF为四面体B-DEF的高，进而求体积.

[规律总结]本题是典型的空间几何问题，图形不是规则的空间几何体，所求的结论是线面平行与垂直以及体积，考查平行关系的判断与性质.解决这类问题，通常利用线线平行证明线面平行，利用线线垂直证明线面垂直，通过求高和底面积求四面体体积.

2.(2010陕西文)18.(本小题满分12分)

如图，在四棱锥P-ABCD中，底面ABCD是矩形PA⊥平面ABCD，AP=AB，BP=BC=2，E，F分别是PB,PC的中点.

　　 (Ⅰ)证明：EF∥平面PAD；

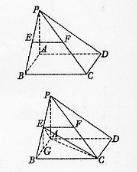　　 (Ⅱ)求三棱锥E-ABC的体积V.

　　 解　 (Ⅰ)在△PBC中，E，F分别是PB，PC的中点，∴EF∥BC.

　　 又BC∥AD,∴EF∥AD,

　　 又∵AD平面PAD,EF平面PAD,

　　 ∴EF∥平面PAD.

(Ⅱ)连接AE,AC,EC,过E作EG∥PA交AB于点G,

　　 则BG⊥平面ABCD,且EG=PA.

　　 在△PAB中，AD=AB,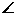PAB°,BP=2,∴AP=AB=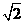,EG=.

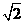　　 ∴S_△ABC=AB·BC=××2=,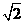

　　 ∴V_E-ABC=S_△ABC·EG=××=.

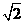1.(2010上海文)20.(本大题满分14分)本题共有2个小题，第1小题满分7分，第2

小题满分7分.

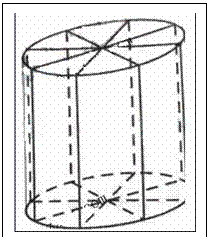如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，再用平方米塑料片制成圆柱的侧面和下底面(不安装上底面).

(1)当圆柱底面半径取何值时，取得最大值？并求出该

最大值(结果精确到0.01平方米);

(2)若要制作一个如图放置的，底面半径为0.3米的灯笼，请作出

用于灯笼的三视图(作图时，不需考虑骨架等因素).

解析：(1) 设圆柱形灯笼的母线长为l，则l=1.2-2r(0<r<0.6)，S=-3p(r-0.4)²+0.48p， 所以当r=0.4时，S取得最大值约为1.51平方米； (2) 当r=0.3时，l=0.6，作三视图略．

7.(2010天津理)(12)一个几何体的三视图如图所示，则这个几何体的体积为　　　　　

[答案]

[解析]本题主要考查三视图的概念与柱体、椎体体积的计算，属于容易题。

由三视图可知，该几何体为一个底面边长为1，高为2的正四棱柱与一个底面边长为2，高为1的正四棱锥组成的组合体，因为正巳灵珠的体积为2，正四棱锥的体积为，所以该几何体的体积V=2+ =

[温馨提示]利用俯视图可以看出几何体底面的形状，结合正视图与侧视图便可得到几何体的形状，求锥体体积时不要丢掉哦。

6.(2010天津文)(12)一个几何体的三视图如图所示，则这个几何体的体积为　　　　　 。

[答案]3

[解析]本题主要考查三视图的基础知识，和主题体积的计算，属于容易题。

由俯视图可知该几何体的底面为直角梯形，则正视图和俯视图可知该几何体的高为1，结合三个试图可知该几何体是底面为直角梯形的直四棱柱，所以该几何题的体积为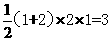

[温馨提示]正视图和侧视图的高是几何体的高，由俯视图可以确定几何体底面的形状，本题也可以将几何体看作是底面是长为3，宽为2，高为1的长方体的一半。

5.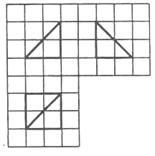(2010辽宁理)(15)如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.

[答案]

[命题立意]本题考查了三视图视角下多面体棱长的最值问题，考查了同学们的识图能力以及由三视图还原物体的能力。

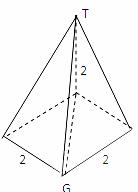[解析]由三视图可知，此多面体是一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥，所以最长棱长为