
题目列表(包括答案和解析)
2.(辽宁卷理24文24)已知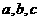 均为正数,证明:
均为正数,证明: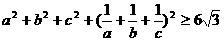 ,并确定
,并确定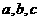 为何值时,等号成立。
为何值时,等号成立。

1.(江苏卷21④)已知实数a,b≥0,求证: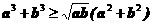
[解析] 本题主要考查证明不等式的基本方法,考查推理论证的能力。满分10分。
(方法一)证明: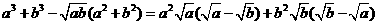
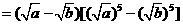
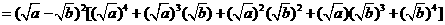
因为实数a、b≥0,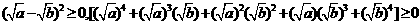
所以上式≥0。即有 。
。
(方法二)证明:由a、b是非负实数,作差得
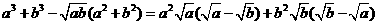
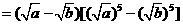
当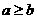 时,
时,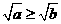 ,从而
,从而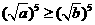 ,得
,得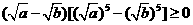 ;
;
当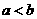 时,
时,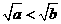 ,从而
,从而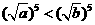 ,得
,得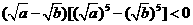 ;
;
所以 。
。
1.(上海春卷16)已知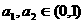 ,记
,记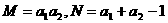 ,则M与N的大小关系是( )
,则M与N的大小关系是( )
A. B.
B.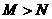 C.
C.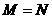 D.不确定
D.不确定
答案:B
解析:由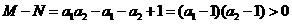 ,故
,故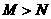 ,选B.
,选B.
4.(上海卷理1文2)不等式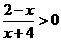 的解集是
。
的解集是
。
[答案](-4,2)
解析:考查分式不等式的解法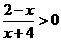 等价于(x-2)(x+4)<0,所以-4<x<2
等价于(x-2)(x+4)<0,所以-4<x<2
3.(全国Ⅰ卷文13)不等式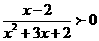 的解集是
.
的解集是
.
[答案]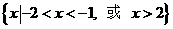
[命题意图]本小题主要考查不等式及其解法
[解析]: 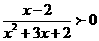
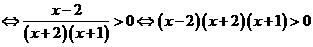 ,数轴标根得:
,数轴标根得: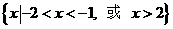
2.(全国Ⅰ卷理13)不等式 的解集是
.
的解集是
.
[答案][0,2]
[命题意图]本小题主要考查根式不等式的解法,利用平方去掉根号是解根式不等式的基本思路,也让转化与化归的数学思想体现得淋漓尽致.
解析:原不等式等价于 解得0≤x≤2.
解得0≤x≤2.
1.(江苏卷11)已知函数 ,则满足不等式
,则满足不等式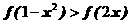 的x的范围是________
的x的范围是________
[答案]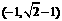
[解析] 考查分段函数的单调性。
7.(天津卷理8)若函数f(x)=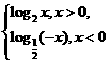 ,若f(a)>f(-a),则实数a的取值范围是
,若f(a)>f(-a),则实数a的取值范围是
(A)(-1,0)∪(0,1) (B)(-∞,-1)∪(1,+∞)
(C)(-1,0)∪(1,+∞) (D)(-∞,-1)∪(0,1)
[答案]C
[解析]当 时,由f(a)>f(-a)得:
时,由f(a)>f(-a)得: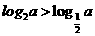 ,即
,即 ,即
,即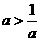 ,
,
解得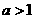 ;当
;当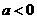 时,由f(a)>f(-a)得:
时,由f(a)>f(-a)得: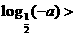
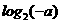 ,即
,即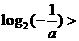
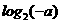 ,
,
即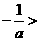
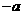 ,解得
,解得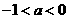 ,故选C。
,故选C。
[命题意图]本小题考查函数求值、不等式求解、对数函数的单调性等基础知识,考查同学们分类讨论的数学思想。
6.(全国Ⅱ卷文2)不等式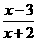 <0的解集为
<0的解集为
(A)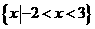 (B)
(B) (C)
(C)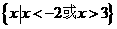 (D)
(D)
[解析]A :本题考查了不等式的解法
∵ 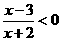 ,∴
,∴  ,故选A
,故选A
5.(全国Ⅱ卷理5)不等式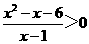 的解集为
的解集为
(A)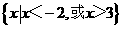 (B)
(B)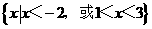
(C)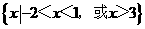 (D)
(D)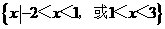
[答案]C
[命题意图]本试题主要考察分式不等式与高次不等式的解法.
[解析]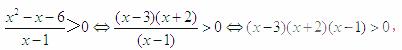 利用数轴穿根法解得-2<x<1或x>3,故选C
利用数轴穿根法解得-2<x<1或x>3,故选C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com