
题目列表(包括答案和解析)
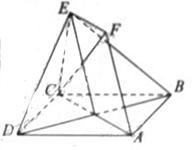
4.(北京卷文16)如图,正方形ABCD和四边形ACEF
所在的平面互相垂直。EF//AC,AB= ,CE=EF=1
,CE=EF=1
(Ⅰ)求证:AF//平面BDE;
(Ⅱ)求证:CF⊥平面BDF;
3.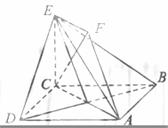 (北京卷理16)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
(北京卷理16)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= ,CE=EF=1.
,CE=EF=1.
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A-BE-D的大小。
证明:(I)设AC与BD交于点G,因为EF∥AG,且EF=1,AG=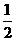 AC=1,所以四边形AGEF为平行四边形。所以AF∥EG。因为EG
AC=1,所以四边形AGEF为平行四边形。所以AF∥EG。因为EG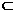 P平面BDE,AF
P平面BDE,AF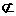 平面BDE,所以AF∥平面BDE。
平面BDE,所以AF∥平面BDE。
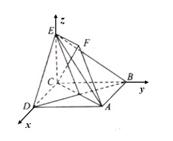 (II)因为正方形ABCD和四边形ACEF所在的平面互相垂直,且CE⊥AC,所以CE⊥AC,所以CE⊥平面ABCD。如图,以C为原点,建立空间直角坐标系C-xyz。则C(0, 0, 0),A(
(II)因为正方形ABCD和四边形ACEF所在的平面互相垂直,且CE⊥AC,所以CE⊥AC,所以CE⊥平面ABCD。如图,以C为原点,建立空间直角坐标系C-xyz。则C(0, 0, 0),A( ,
, ,0),D(
,0),D( ,0, 0),E(0, 0, 1),F(
,0, 0),E(0, 0, 1),F(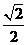 ,
,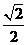 ,1)。所以
,1)。所以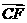 =(
=(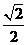 ,
,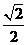 ,1),
,1),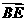 =(0,-
=(0,- ,1),
,1),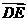 =(-
=(- ,0,1)。所以
,0,1)。所以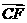 ·
·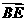 =
0-1+1=0,
=
0-1+1=0,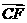 ·
·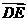 =-1+0+1=0。所以CF⊥BE,CF⊥DE,所以CF⊥平面BDE
=-1+0+1=0。所以CF⊥BE,CF⊥DE,所以CF⊥平面BDE
(III)由(II)知,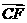 =(
=(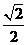 ,
,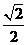 ,1),是平面BDE的一个法向量,设平面ABE的法向量
,1),是平面BDE的一个法向量,设平面ABE的法向量 =(x,y,z),则
=(x,y,z),则 ·
·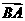 =0,
=0, ·
·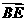 =0。
=0。
即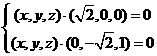
所以x=0,且z= y。令y=1,则z=
y。令y=1,则z= 。所以n=(
。所以n=(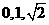 ),从而cos(
),从而cos( ,
,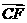 )=
)=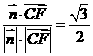
 因为二面角A-BE-D为锐角,所以二面角A-BE-D为
因为二面角A-BE-D为锐角,所以二面角A-BE-D为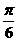 。
。
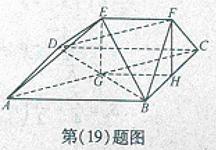
2.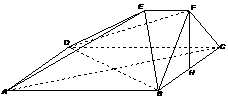 (安徽卷文19)如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
(安徽卷文19)如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
(Ⅰ)求证:FH∥平面EDB;
(Ⅱ)求证:AC⊥平面EDB;
(Ⅲ)求四面体B-DEF的体积;
 [命题意图]本题考查空间线面平行、线面垂直、面面垂直的判断与证明,考查体积的计算等基础知识,同时考查空间想象能力、推理论证能力和运算能力.
[命题意图]本题考查空间线面平行、线面垂直、面面垂直的判断与证明,考查体积的计算等基础知识,同时考查空间想象能力、推理论证能力和运算能力.
[解题指导](1)设底面对角线交点为G,则可以通过证明EG∥FH,得 ∥平面
∥平面 ;(2)利用线线、线面的平行与垂直关系,证明FH⊥平面ABCD,得FH⊥BC,FH⊥AC,进而得EG⊥AC,
;(2)利用线线、线面的平行与垂直关系,证明FH⊥平面ABCD,得FH⊥BC,FH⊥AC,进而得EG⊥AC, 平面
平面 ;(3)证明BF⊥平面CDEF,得BF为四面体B-DEF的高,进而求体积.
;(3)证明BF⊥平面CDEF,得BF为四面体B-DEF的高,进而求体积.


[规律总结]本题是典型的空间几何问题,图形不是规则的空间几何体,所求的结论是线面平行与垂直以及体积,考查平行关系的判断与性质.解决这类问题,通常利用线线平行证明线面平行,利用线线垂直证明线面垂直,通过求高和底面积求四面体体积.
1.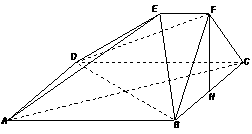 (安徽卷理18)如图,在多面体
(安徽卷理18)如图,在多面体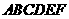 中,四边形
中,四边形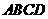 是正方形,
是正方形, ∥
∥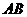 ,
,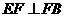 ,
,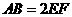 ,
,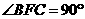 ,
,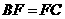 ,
,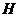 为
为 的中点。
的中点。
(Ⅰ)求证: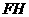 ∥平面
∥平面 ;
;
(Ⅱ)求证: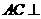 平面
平面 ;
;
(Ⅲ)求二面角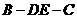 的大小。
的大小。



1.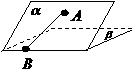 (四川卷理15文15)如图,二面角
(四川卷理15文15)如图,二面角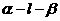 的大小是60°,线段
的大小是60°,线段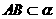 .
.
 ,
,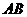 与
与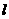 所成的角为30°.则
所成的角为30°.则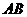 与平面
与平面 所成的角的正弦值是 .
所成的角的正弦值是 .
解析:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D
连结AD,有三垂线定理可知AD⊥l,
故∠ADC为二面角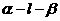 的平面角,为60°
的平面角,为60°
又由已知,∠ABD=30°
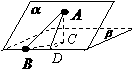 连结CB,则∠ABC为
连结CB,则∠ABC为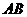 与平面
与平面 所成的角
所成的角
设AD=2,则AC=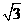 ,CD=1
,CD=1
AB=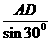 =4
=4
∴sin∠ABC=
答案: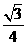
6.(重庆卷文9)到两互相垂直的异面直线的距离相等的点
(A)只有1个 (B)恰有3个
(C)恰有4个 (D)有无穷多个
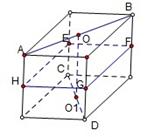 [答案]D
[答案]D
[解析]放在正方体中研究,显然,线段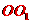 、EF、FG、GH、
、EF、FG、GH、
HE的中点到两垂直异面直线AB、CD的距离都相等,
所以排除A、B、C,选D
亦可在四条侧棱上找到四个点到两垂直异面直线AB、CD的距离相等
5.(重庆卷理10)到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是
A. 直线 B. 椭圆 C. 抛物线 D. 双曲线
[答案]D
解析:排除法 轨迹是轴对称图形,排除A、C,轨迹与已知直线不能有交点,排除B
4.(全国Ⅱ卷文8)已知三棱锥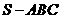 中,底面
中,底面 为边长等于2的等边三角形,
为边长等于2的等边三角形,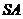 垂直于底面
垂直于底面 ,
,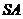 =3,那么直线
=3,那么直线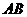 与平面
与平面 所成角的正弦值为
所成角的正弦值为
(A)
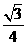 (B)
(B)
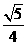 (C)
(C) 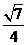 (D)
(D)
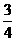
[答案]D:
[命题意图]本题考查了立体几何的线与面、面与面位置关系及直线与平面所成角。
[解析]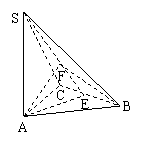 过A作AE垂直于BC交BC于E,连结SE,过A作AF垂直于SE交SE于F,连BF,∵正三角形ABC,∴ E为BC中点,∵ BC⊥AE,SA⊥BC,∴ BC⊥面SAE,∴ BC⊥AF,AF⊥SE,∴ AF⊥面SBC,∵∠ABF为直线AB与面SBC所成角,由正三角形边长3,∴
过A作AE垂直于BC交BC于E,连结SE,过A作AF垂直于SE交SE于F,连BF,∵正三角形ABC,∴ E为BC中点,∵ BC⊥AE,SA⊥BC,∴ BC⊥面SAE,∴ BC⊥AF,AF⊥SE,∴ AF⊥面SBC,∵∠ABF为直线AB与面SBC所成角,由正三角形边长3,∴
 ,AS=3,∴ SE=
,AS=3,∴ SE=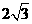 ,AF=
,AF=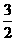 ,∴
,∴
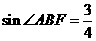
3.(全国Ⅱ卷理11文11)与正方体ABCD-A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点
(A)有且只有1个 (B)有且只有2个
(C)有且只有3个 (D)有无数个
[答案]D
[解析]直线 上取一点,分别作
上取一点,分别作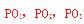 垂直于
垂直于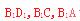 于
于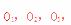 则
则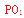

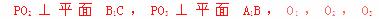 分别作
分别作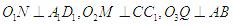 ,垂足分别为M,N,Q,连PM,PN,PQ,由三垂线定理可得,PN⊥
,垂足分别为M,N,Q,连PM,PN,PQ,由三垂线定理可得,PN⊥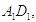 PM⊥
PM⊥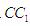 ;PQ⊥AB,由于正方体中各个表面、对等角全等,所以
;PQ⊥AB,由于正方体中各个表面、对等角全等,所以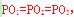
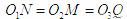 ,∴PM=PN=PQ,即P到三条棱AB、CC1、A1D1.所在直线的距离相等所以有无穷多点满足条件,故选D.
,∴PM=PN=PQ,即P到三条棱AB、CC1、A1D1.所在直线的距离相等所以有无穷多点满足条件,故选D.
2.(全国Ⅰ卷文6)直三棱柱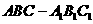 中,若
中,若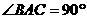 ,
,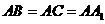 ,则异面直线
,则异面直线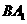 与
与 所成的角等于
所成的角等于
(A)30° (B)45° (C)60° (D)90°
[答案]C
[命题意图]本小题主要考查直三棱柱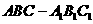 的性质、异面直线所成的角、异面直线所成的角的求法.
的性质、异面直线所成的角、异面直线所成的角的求法.
[解析]延长CA到D,使得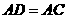 ,则
,则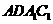 为平行四边形,
为平行四边形,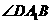 就是异面直线
就是异面直线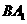 与
与 所成的角,又三角形
所成的角,又三角形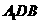 为等边三角形,
为等边三角形,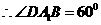
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com