
题目列表(包括答案和解析)
3.(全国Ⅱ卷理15文15)已知抛物线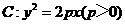 的准线为
的准线为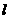 ,过
,过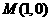 且斜率为
且斜率为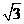 的直线与
的直线与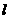 相交于点
相交于点 ,与
,与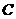 的一个交点为
的一个交点为 .若
.若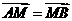 ,则
,则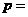 .
.
[答案]2
[命题意图]本题主要考查抛物线的定义与性质.
[解析]过B作BE垂直于准线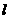 于E,∵
于E,∵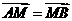 ,∴M为中点,
,∴M为中点,
∴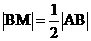 ,又斜率为
,又斜率为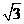 ,
,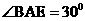 ,
,
∴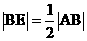 ,∴
,∴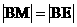 ,
,
∴M为抛物线的焦点,∴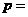 2.
2.
2.(湖南卷理14)过抛物线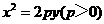 的焦点作斜率为1的直线与该抛物线交于
的焦点作斜率为1的直线与该抛物线交于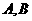 两点,
两点,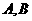 在
在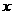 轴上的正射影分别为
轴上的正射影分别为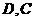 .若梯形
.若梯形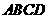 的面积为
的面积为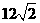 ,则
,则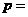 .
.
[答案]2
[解析]抛物线的焦点坐标为F(0,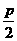 ),则过焦点斜率为1的直线方程为
),则过焦点斜率为1的直线方程为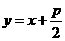 ,
,
设A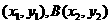 (
(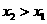 ),由题意可知
),由题意可知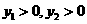
由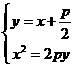 ,消去y得
,消去y得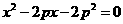 ,
,
由韦达定理得,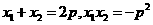
所以梯形ABCD的面积为:
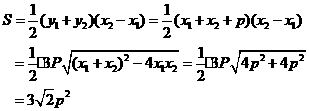
所以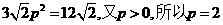
[命题意图]本题考查抛物线的焦点坐标,直线的方程,直线与抛物线的位置关系,考察考生的运算能力,属中档题
1.(安徽卷文12)抛物线y2=8x的焦点坐标是
[答案].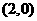
[解析]抛物线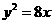 ,所以
,所以 ,所以焦点
,所以焦点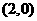 .
.
[误区警示]本题考查抛物线的交点.部分学生因不会求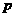 ,或求出
,或求出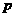 后,误认为焦点
后,误认为焦点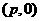 ,还有没有弄清楚焦点位置,从而得出错误结论.
,还有没有弄清楚焦点位置,从而得出错误结论.
7.(上海春卷17)已知抛物线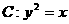 与直线
与直线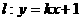 ,“
,“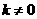 ”是“直线l与抛物线C有两个不同交点”的 ( )
”是“直线l与抛物线C有两个不同交点”的 ( )
A.充分不必要条件 B.必要不充分条件;
C.充要条件 D.既不充分也不必要条件
答案:B
解析:由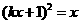 即
即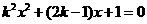 ,
,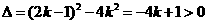 ,则
,则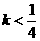 。故“
。故“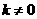 ”推不出“直线
”推不出“直线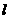 与抛物线
与抛物线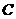 有两个不同的交点”,但“直线
有两个不同的交点”,但“直线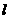 与抛物线
与抛物线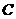 有两个不同的交点”则必有“
有两个不同的交点”则必有“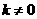 ”。故选B.
”。故选B.
6.(四川卷文3)抛物线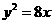 的焦点到准线的距离是( )高^考#资*源^网
的焦点到准线的距离是( )高^考#资*源^网
(A) 1 (B)2 (C)4 (D)8
解析:由y2=2px=8x知p=4 又交点到准线的距离就是p
答案:C
5.(陕西卷理8文9)已知抛物线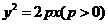 的准线与圆
的准线与圆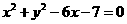 相切,则p的值为[ ]
相切,则p的值为[ ]
A. 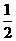 B.
1
C.2
D.4
B.
1
C.2
D.4
[答案]C
[解析]由题设知,直线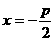 与圆
与圆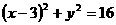 相切,从而
相切,从而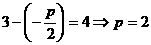 .故选
.故选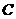 .
.
4. (山东卷文9)已知抛物线
(山东卷文9)已知抛物线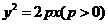 ,过其焦点且斜率为1的直线交抛物线与
,过其焦点且斜率为1的直线交抛物线与 、
、 两点,若线段
两点,若线段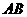 的中点的纵坐标为2,则该抛物线的准线方程为
的中点的纵坐标为2,则该抛物线的准线方程为
(A)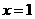 (B)
(B)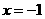 (C)
(C)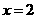 (D)
(D)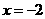
[答案]B
[解析]设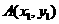 、
、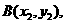 则有
则有 ,
,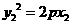 ,两式相减得:
,两式相减得:
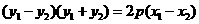 ,又因为直线的斜率为1,所以
,又因为直线的斜率为1,所以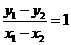 ,所以有
,所以有
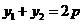 ,又线段
,又线段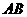 的中点的纵坐标为2,即
的中点的纵坐标为2,即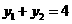 ,所以
,所以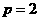 ,所以抛物线的准线方程为
,所以抛物线的准线方程为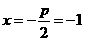 。
。
[命题意图]本题考查抛物线的几何性质、直线与抛物线的位置关系等基础知识,
3.(辽宁卷理7文7)设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的斜率为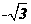 ,那么|PF|=
,那么|PF|=
(A)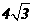 (B)8 (C)
(B)8 (C)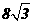 (D)
16
(D)
16
2.(湖南卷文5)设抛物线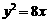 上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是
上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是
A. 4 B. 6 C. 8 D. 12
[答案]B
[解析]抛物线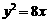 的准线为x= -2,点P到y轴的距离是4,到准线的距离是6,点P到该抛物线焦点的距离是6
的准线为x= -2,点P到y轴的距离是4,到准线的距离是6,点P到该抛物线焦点的距离是6
1.(福建卷理2)以抛物线 的焦点为圆心,且过坐标原点的圆的方程为
的焦点为圆心,且过坐标原点的圆的方程为
A.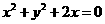 B.
B.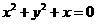
C.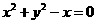 D.
D.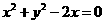
[答案]D
[解析]因为已知抛物线的焦点坐标为(1,0),即所求圆的圆心,又圆过原点,所以圆的半径为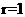 ,故所求圆的方程为
,故所求圆的方程为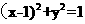 ,即
,即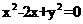 ,选D。
,选D。
[命题意图]本题考查抛物线的几何性质以及圆的方程的求法,属基础题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com