
题目列表(包括答案和解析)
12.(重庆卷理5)函数 的图象
的图象
A. 关于原点对称 B. 关于直线y=x对称 C. 关于x轴对称 D. 关于y轴对称
[答案]D
解析: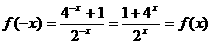
 是偶函数,图像关于y轴对称
是偶函数,图像关于y轴对称
11.(天津卷文5)下列命题中,真命题是
(A)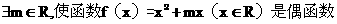
(B)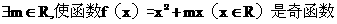
(C)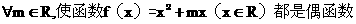
(D)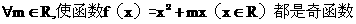
[答案]A
[解析]当m=0时,函数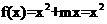 是偶函数,故A正确。
是偶函数,故A正确。
10.(天津卷理3)命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是
(A)若f(x) 是偶函数,则f(-x)是偶函数
(B)若f(x)不是奇函数,则f(-x)不是奇函数
(C)若f(-x)是奇函数,则f(x)是奇函数
(D)若f(-x)不是奇函数,则f(x)不是奇函数
[答案]B
[解析]因为一个命题的否命题是只对其结论进行否定,所以选B。
[命题意图]本小题考查简易逻辑中的否命题的写法,属基础题。
9.(山东卷理4文5)设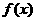 为定义在R上的奇函数。当x≥0时,
为定义在R上的奇函数。当x≥0时,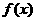 =
=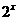 +2x+b(b为常数),则
+2x+b(b为常数),则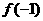 =
=
(A)3 (B)1 (C)-1 (D)-3
[答案]D
[解析]因为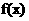 为定义在R上的奇函数,所以有
为定义在R上的奇函数,所以有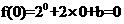 ,解得
,解得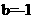 ,所以
,所以
当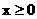 时,
时, 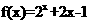 ,即
,即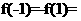
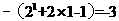 ,故选D.
,故选D.
[命题意图]本题考查函数的基本性质,熟练函数的基础知识是解答好本题的关键.
8.(全国Ⅱ卷文4)函数y=1+ln(x-1)(x>1)的反函数是
(A)y=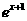 -1(x>0)
(B)y=
-1(x>0)
(B)y=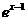 +1(x>0)
+1(x>0)
(C) y=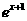 -1(x
-1(x 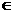 R)
(D)y=
R)
(D)y=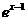 +1 (x
+1 (x 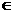 R)
R)
[解析]D:本题考查了函数的反函数及指数对数的互化,∵函数y=1+ln(x-1)(x>1),∴ 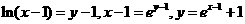
7.(全国Ⅱ卷理2)函数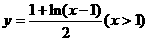 的反函数是
的反函数是
(A)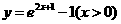 (B)
(B)
(C)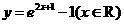 (D)
(D)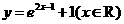
[答案]D
[命题意图]本试题主要考察反函数的求法及指数函数与对数函数的互化。
[解析]由原函数解得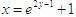 ,即
,即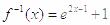 ,又
,又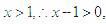 ;
;
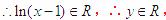 ∴在反函数中
∴在反函数中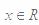 ,故选D.
,故选D.
6. (全国Ⅰ新卷理5)已知命题
 :函数
:函数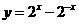 在R为增函数,
在R为增函数,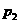 :函数
:函数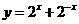 在R为减函数,
在R为减函数,
则在命题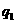 :
: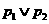 ,
,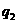 :
: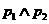 ,
,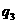 :
: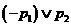 和
和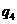 :
: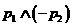 中,真命题是
中,真命题是
(A)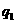 ,
,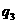 (B)
(B)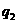 ,
,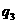 (C)
(C)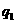 ,
,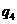 (D)
(D)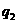 ,
,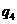
[答案]C
解析:易知 是真命题,而对
是真命题,而对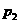 :
: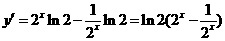 ,当
,当 时,
时,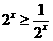 ,又
,又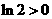 ,所以
,所以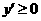 ,函数单调递增;同理得当
,函数单调递增;同理得当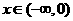 时,函数单调递减,故
时,函数单调递减,故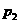 是假命题.由此可知,
是假命题.由此可知,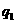 真,
真,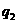 假,
假,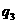 假,
假,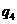 真.
真.
另解:对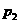 的真假可以取特殊值来判断,如取
的真假可以取特殊值来判断,如取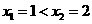 ,得
,得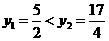 ;取
;取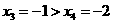 ,得
,得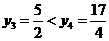 即可得到
即可得到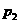 是假命题,下略.
是假命题,下略.
5.(江西卷文8)若函数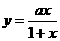 的图像关于直线
的图像关于直线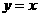 对称,则
对称,则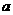 为
为
A.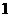 B.
B.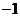 C.
C.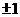 D.任意实数
D.任意实数
[答案]B
[解析]考查反函数,因为图像本身关于直线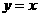 对称故可知原函数与反函数是同一函数,所以先求反函数再与原函数比较系数可得答案。
对称故可知原函数与反函数是同一函数,所以先求反函数再与原函数比较系数可得答案。
或利用反函数的性质,依题知(1,a/2)与(a/2,1)皆在原函数图故可得a=-1
4.(江西卷理9)给出下列三个命题:
①函数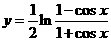 与
与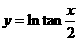 是同一函数;
是同一函数;
②若函数 与
与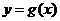 的图像关于直线
的图像关于直线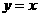 对称,则函数
对称,则函数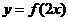 与
与 的图像也关于直线
的图像也关于直线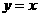 对称;
对称;
③若奇函数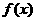 对定义域内任意
对定义域内任意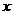 都有
都有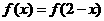 ,则
,则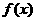 为周期函数.
为周期函数.
其中真命题是
A.①② B.①③ C.②③ D.②
[答案]C
[解析]考查相同函数、函数对称性的判断、周期性知识。考虑定义域不同,①错误;排除A、B,验证③, 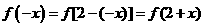 ,又通过奇函数得
,又通过奇函数得 ,所以f(x)是周期为2的周期函数,选择C。
,所以f(x)是周期为2的周期函数,选择C。
3. (广东卷理3文3)若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则
(广东卷理3文3)若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则
A.f(x)与g(x)均为偶函数 B. f(x)为偶函数,g(x)为奇函数
C.f(x)与g(x)均为奇函数 D. f(x)为奇函数,g(x)为偶函数
[答案]D.
[解析]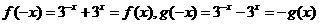 .故f(x)为奇函数,g(x)为偶函数
.故f(x)为奇函数,g(x)为偶函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com