
题目列表(包括答案和解析)
8.(浙江卷文19)设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足 +15=0。
+15=0。
(Ⅰ)若 =5,求
=5,求 及a1;
及a1;
(Ⅱ)求d的取值范围。
解析:本题主要考查等差数列概念、求和公式等基础知识,同时考查运算求解能力及分析问题解决问题的能力。
(Ⅰ)解:由题意知S6= =-3,
=-3,
A6=S6-S5=-8
所以
解得a1=7
所以S6= -3,a1=7
(Ⅱ)解:因为S5S6+15=0,
所以(5a1+10d)(6a1+15d)+15=0,
即2a12+9da1+10d2+1=0.
故(4a1+9d)2=d2-8.
所以d2≥8.[
故d的取值范围为d≤-2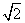 或d≥2
或d≥2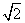 .
.
7.(四川卷文20)已知等差数列 的前3项和为6,前8项和为-4。
的前3项和为6,前8项和为-4。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前n项和
的前n项和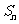

6. (陕西卷理16文16)已知{an}是公差不为零的等差数列,a1=1,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项;
(Ⅱ)求数列{2an}的前n项和Sn.
解 由题设知公差
由题设知公差
由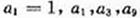 成等比数列得
成等比数列得
解得 (舍去)
(舍去)
故 的通项
的通项
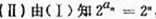 ,
,
由等比数列前n项和公式得
5.(山东卷文18)已知等差数列 满足:
满足: ,
, .
. 的前n项和为
的前n项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)令 (
( ),求数列
),求数列 的前n项和
的前n项和 .
.
[命题意图]本题考查等差数列的通项公式与前n项和公式的应用、裂项法求数列的和,熟练数列的基础知识是解答好本类题目的关键。
[解析](Ⅰ)设等差数列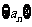 的公差为d,因为
的公差为d,因为 ,
, ,所以有
,所以有
 ,解得
,解得 ,
,
所以 ;
;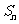 =
= =
= 。
。
(Ⅱ)由(Ⅰ)知 ,所以bn=
,所以bn= =
=
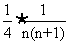 =
= ,
,
所以 =
= =
=
 ,
,
即数列 的前n项和
的前n项和 =
= 。
。
4.(山东卷理18)已知等差数列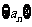 满足:
满足: ,
, ,
,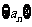 的前n项和为
的前n项和为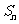 .
.
(Ⅰ)求 及
及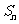 ;
;
(Ⅱ)令bn= (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
.
[解析](Ⅰ)设等差数列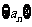 的公差为d,因为
的公差为d,因为 ,
, ,所以有
,所以有
 ,解得
,解得 ,
,
所以 ;
;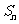 =
= =
= 。
。
(Ⅱ)由(Ⅰ)知 ,所以bn=
,所以bn= =
=
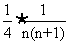 =
= ,
,
所以 =
= =
=
 ,
,
即数列 的前n项和
的前n项和 =
= 。
。
[命题意图]本题考查等差数列的通项公式与前n项和公式的应用、裂项法求数列的和,熟练数列的基础知识是解答好本类题目的关键。
3.(全国Ⅰ新卷文17)设等差数列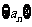 满足
满足 ,
, 。
。
(Ⅰ)求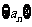 的通项公式;
的通项公式;
(Ⅱ)求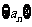 的前
的前 项和
项和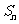 及使得
及使得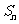 最大的序号
最大的序号 的值。
的值。
解: (1)由am = a1 +(n-1)d及a1=5,aw=-9得
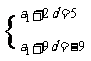 解得
解得
数列{am}的通项公式为an=11-2n。 ……..6分
(2)由(1) 知Sm=na1+ d=10n-n2。
d=10n-n2。
因为Sm=-(n-5)2+25.
所以n=5时,Sm取得最大值。 ……12分
2. (全国Ⅰ卷文17)记等差数列
(全国Ⅰ卷文17)记等差数列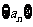 的前
的前 项和为
项和为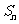 ,设
,设 ,且
,且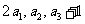 成等比数列,求
成等比数列,求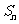 .
.

1.(北京卷文16)已知 为等差数列,且
为等差数列,且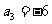 ,
,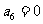 。
。
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若等差数列 满足
满足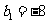 ,
,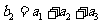 ,求
,求 的前n项和公式
的前n项和公式

3.(浙江卷文14)在如下数表中,已知每行、每列中的树都成等差数列,那么,位于下表中的第n行第n+1列的数是 。

解析:第n行第一列的数为n,观察得,第n行的公差为n,所以第n0行的通项公式为

 ,又因为为第n+1列,故可得答案为
,又因为为第n+1列,故可得答案为 ,本题主要考察了等差数列的概念和通项公式,以及运用等差关系解决问题的能力,属中档题。
,本题主要考察了等差数列的概念和通项公式,以及运用等差关系解决问题的能力,属中档题。
2. (浙江卷理15)设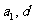 为实数,首项为
为实数,首项为 ,公差为
,公差为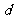 的等差数列
的等差数列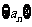 的前
的前 项和为
项和为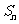 ,满足
,满足 ,则
,则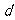 的取值范围是__________________ .
的取值范围是__________________ .
解析:因为
 所以(5a1+10d)(6a1+15d)=0,即
所以(5a1+10d)(6a1+15d)=0,即 ,故
,故 ,则
,则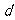 的取值范围是
的取值范围是 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com