3.(福建卷文14)将容量为n的样本中的数据分成6组. 绘制频率分步直方图.若第一组至第六组数据的频率之比为2：3：4：6：4：1，且前三组数据的频率之和等于27，则n等于　　　 .

[答案]60

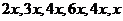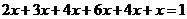[解析]设第一组至第六组数据的频率分别为，则，解得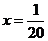，所以前三组数据的频率分别是，

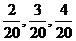故前三组数据的频数之和等于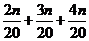=27，解得n=60。

[命题意图]本小题考查频率分布直方图的基础知识，熟练基本公式是解答好本题的关键。

2.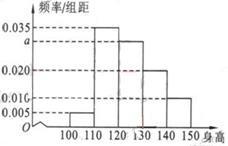(北京卷理11文12)从某小学随机抽取100名同学，将他们的身高(单位：厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a＝　　　　　 。若要从身高在[ 120 , 130)，[130 ，140) , [140 , 150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140 ，150]内的学生中选取的人数应为　　　　 。

[答案]0.030， 3

解析：由所有小矩形面积为1不难得到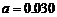，而三组身高区间的人数比为3:2:1，由分层抽样的原理不难得到140-150区间内的人数为3人。

1.(安徽卷文14)某地有居民100 000户，其中普通家庭99 000户,高收入家庭1 000户．从普通家庭中以简单随机抽样方式抽取990户，从高收入家庭中以简单随机抽样方式抽取l00户进行调查，发现共有120户家庭拥有3套或3套以上住房，其中普通家庭50户，高收人家庭70户．依据这些数据并结合所掌握的统计知识，你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是　 　　　　　　　.

[答案]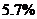

[解析]该地拥有3套或3套以上住房的家庭可以估计有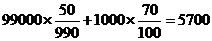：户，

所以所占比例的合理估计是.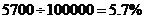

[方法总结]本题分层抽样问题，首先根据拥有3套或3套以上住房的家庭所占的比例，得出100 000户，居民中拥有3套或3套以上住房的户数，它除以100 000得到的值，为该地拥有3套或3套以上住房的家庭所占比例的合理估计.

13.(重庆卷文17)在甲、乙等6个单位参加的一次“唱读讲传”演出活动中，每个单位的节目集中安排在一起.若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……6)，求：

(Ⅰ)甲、乙两单位的演出序号均为偶数的概率；

(Ⅱ)甲、乙两单位的演出序号不相邻的概率.

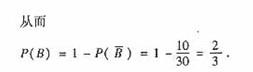
12.(天津卷文18)有编号为,,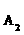…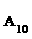的10个零件，测量其直径(单位：cm)，得到下面数据：

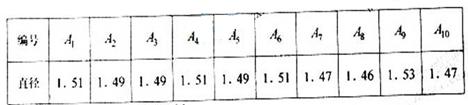
其中直径在区间[1.48，1.52]内的零件为一等品。

(Ⅰ)从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；

(Ⅱ)从一等品零件中，随机抽取2个.

　　 (ⅰ)用零件的编号列出所有可能的抽取结果；

　　 (ⅱ)求这2个零件直径相等的概率。

[命题意图]本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力。

[解析](Ⅰ)解：由所给数据可知，一等品零件共有6个.设“从10个零件中，随机抽取一个为一等品”为事件A，则P(A)==.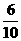

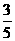(Ⅱ)(i)解：一等品零件的编号为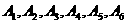.从这6个一等品零件中随机抽取2个，所有可能的结果有：,,,

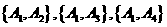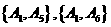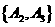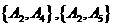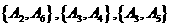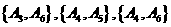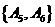,,,共有15种.

　(ii)解：“从一等品零件中，随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有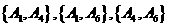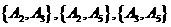：，，共有6种.

　　　 所以P(B)=.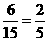

11.(四川卷文17)某种有奖销售的饮料，瓶盖内印有“奖励一瓶”或“谢谢购买”字样，购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖，中奖概率为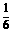.甲、乙、丙三位同学每人购买了一瓶该饮料。

(Ⅰ)求三位同学都没有中奖的概率；

(Ⅱ)求三位同学中至少有两位没有中奖的概率.

10.(陕西卷理19)为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行出样检查，测得身高情况的统计图如下：

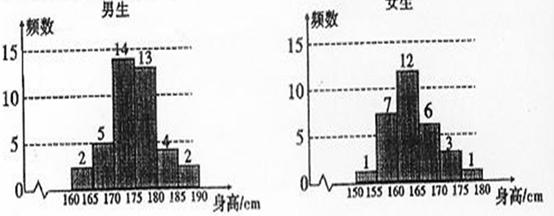
(Ⅰ)估计该校男生的人数；

(Ⅱ)估计该校学生身高在170~185cm之间的概率；

(III)从样本中身高在165~180cm之间的女生中任选2人，求至少有1人身高在170~180cm之间的概率。

解(Ⅰ)样本中男生人数为40 ，由分层出样比例为10%估计全校男生人数为400。

(Ⅱ)有统计图知，样本中身高在170~185cm之间的学生有14+13+4+3+1=35人，样本容量为70 ，所以样本中学生身高在170~185cm之间的频率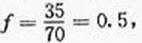故有f估计该校学生身高在170~180cm之间的概率

(III)样本中女生身高在165~180cm之间的人数为10，身高在170~180cm之间的人数为4。

设A表示事件“从样本中身高在165~180cm之间的女生中任选2人，求至少有1人身高在170~180cm之间”，则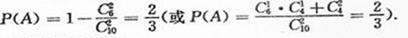

9.(山东卷文19)一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4.

(Ⅰ)从袋中随机抽取两个球，求取出的球的编号之和不大于4的概率；

(Ⅱ)先从袋中随机取一个球，该球的编号为m，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n，求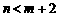的概率.

[命题意图]本小题主要考察古典概念、对立事件的概率计算，考察学生分析问题、解决问题的能力。

[解析](I)从袋子中随机取两个球，其一切可能的结果组成的基本事件有1和2，1和3，1和4，2和3，2和4，3和4，共6个。

从袋中随机取出的球的编号之和不大于4的事件共有1和2,1和3两个。

因此所求事件的概率为1/3。

(II)先从袋中随机取一个球，记下编号为m，放回后，在从袋中随机取一个球，记下编号为n，其一切可能的结果(m, n)有：

(1,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1)(3,2), (3,3) (3,4),(4,1) (4,2)，(4,3)(4,4)，共16个

有满足条件n≥　m+2 的事件为(1,3) (1,4) (2,4)，共3个

所以满足条件n ≥ m+2 的事件的概率为　 P=3/16

故满足条件n<m+2 的事件的概率为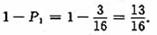　

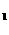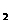8.(全国Ⅱ卷文20)如图，由M到N的电路中有4个元件，分别标为T，T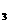，T，T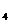，电源能通过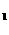T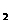，T，T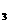的概率都是P，电源能通过T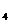的概率是0.9，电源能否通过各元件相互独立。已知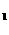T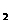，T，T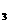中至少有一个能通过电流的概率为0.999。

(Ⅰ)求P；

(Ⅱ)求电流能在M与N之间通过的概率。

[分析]本题考查了概率中的互斥事件、对立事件及独立事件的概率，

(1)设出基本事件，将要求事件用基本事件的来表示，将T1，T2，T3至少有一个能通过电流用基本事件表示并求出概率即可求得p。

(2)将MN之间能通过电流用基本事件表示出来，由互斥事件与独立事件的概率求得。

[解析]记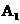表示事件：电流能通过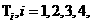

A表示事件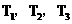：中至少有一个能通过电流，

B表示事件：电流能在M与N之间通过，

(Ⅰ)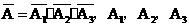相互独立，

　 　　,

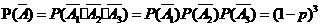又　　 ，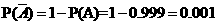

故　　 ，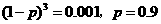

(Ⅱ)，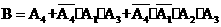

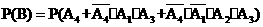
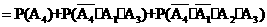
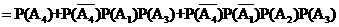
　　　　　 =0.9+0.1×0.9×0.9+0.1×0.1×0.9×0.9

　　　　　 =0.9891

7.(全国Ⅰ卷文19)投到某杂志的稿件，先由两位初审专家进行评审．若能通过两位初审专家的评审，则予以录用；若两位初审专家都未予通过，则不予录用；若恰能通过一位初审专家的评审，则再由第三位专家进行复审，若能通过复审专家的评审，则予以录用，否则不予录用．设稿件能通过各初审专家评审的概率均为0.5，复审的稿件能通过评审的概率为0.3．

各专家独立评审．

　　 (I)求投到该杂志的1篇稿件被录用的概率；

　　 (II)求投到该杂志的4篇稿件中，至少有2篇被录用的概率．

解：　 (Ⅰ)记 A表示事件：稿件能通过两位初审专家的评审；

　　　　　　 B表示事件：稿件恰能通过一位初审专家的评审；

　　　　　　 C表示事件：稿件能通过复审专家的评审；

　　　　　　 D表示事件：稿件被录用.

　 则　 D=A+B·C,

　　　　　　　 =

　　　　　　　 =

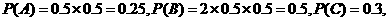
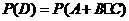
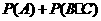
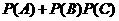
　　　　　　　 =0.25+0.5×0.3

　　　　　　　 =0.40.