
题目列表(包括答案和解析)
6.(2010安徽文数)(3)设向量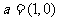 ,
,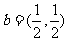 ,则下列结论中正确的是
,则下列结论中正确的是
(A)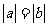 (B)
(B)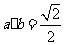
(C)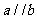 (D)
(D) 与
与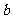 垂直
垂直

 w_w w. k#s5_
w_w w. k#s5_
[答案]D
[解析]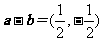 ,
,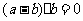 ,所以
,所以 与
与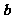 垂直.
垂直.
[规律总结]根据向量是坐标运算,直接代入求解,判断即可得出结论.
5.(2010全国卷2文数)(10)△ABC中,点D在边AB上,CD平分∠ACB,若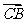 = a ,
= a , 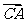 = b ,
= b , 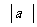 = 1 ,
= 1 ,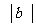 = 2, 则
= 2, 则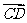 =
=

 w_w w. k#s5_
w_w w. k#s5_
(A)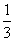 a +
a + 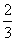 b (B)
b (B)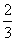 a +
a +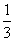 b (C)
b (C)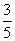 a +
a +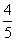 b
(D)
b
(D)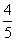 a +
a +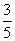 b
b
[答案]B
[解析]本题考查了平面向量的基础知识
∵ CD为角平分线,∴ 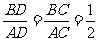 ,∵
,∵ 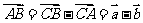 ,∴
,∴ 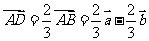 ,∴
,∴ 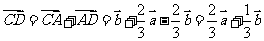
4.(2010辽宁理数)(8)平面上O,A,B三点不共线,设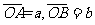 ,则△OAB的面积等于
,则△OAB的面积等于
(A)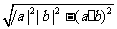 (B)
(B) 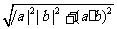


 w_w w. k#s5_
w_w w. k#s5_
(C) 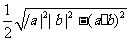 (D)
(D) 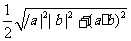
[答案]C
[命题立意]本题考查了三角形面积的向量表示,考查了向量的内积以及同角三角函数的基本关系。
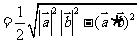
[解析]三角形的面积S=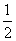 |a||b|sin<a,b>,而
|a||b|sin<a,b>,而

 w_w w. k#s5_
w_w w. k#s5_
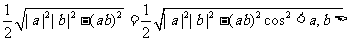
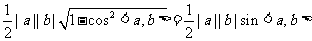
3.(2010辽宁文数)(8)平面上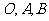 三点不共线,设
三点不共线,设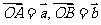 ,则
,则 的面积等于
的面积等于 

 w_w w. k#s5_
w_w w. k#s5_
K^S*5U.C#
(A)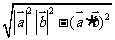 (B)
(B)
(C)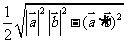 (D)
(D)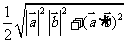
答案:C
解析:选C. 

 w_w w. k#s5_
w_w w. k#s5_
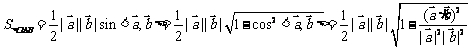
2.(2010全国卷2理数)(8)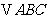 中,点
中,点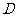 在
在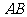 上,
上,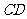 平方
平方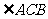 .若
.若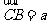 ,
,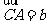 ,
,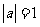 ,
,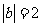 ,则
,则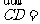
(A)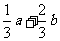 (B)
(B)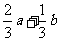 (C)
(C)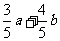 (D)
(D)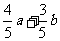
[答案]B
[命题意图]本试题主要考查向量的基本运算,考查角平分线定理.
[解析]因为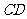 平分
平分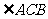 ,由角平分线定理得
,由角平分线定理得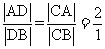 ,所以D为AB的三等分点,且
,所以D为AB的三等分点,且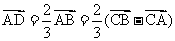 ,所以
,所以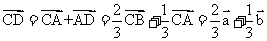 ,故选B.
,故选B.
1.(2010湖南文数)6. 若非零向量a,b满足|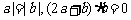 ,则a与b的夹角为
,则a与b的夹角为
A. 300 B. 600 C. 1200 D. 1500
答案:C
6.(2010安徽理数)7、设曲线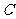 的参数方程为
的参数方程为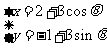 (
(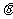 为参数),直线
为参数),直线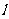 的方程为
的方程为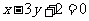 ,则曲线
,则曲线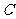 上到直线
上到直线 距离为
距离为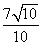 的点的个数为
的点的个数为

 w_w w. k#s5_
w_w w. k#s5_
A、1 B、2 C、3 D、4
[答案]B
[解析]化曲线 的参数方程为普通方程:
的参数方程为普通方程: ,圆心
,圆心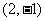 到直线
到直线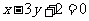 的距离
的距离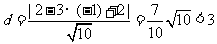 ,直线和圆相交,过圆心和
,直线和圆相交,过圆心和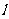 平行的直线和圆的2个交点符合要求,又
平行的直线和圆的2个交点符合要求,又 ,在直线
,在直线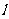 的另外一侧没有圆上的点符合要求,所以选B.
的另外一侧没有圆上的点符合要求,所以选B.
[方法总结]解决这类问题首先把曲线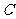 的参数方程为普通方程,然后利用圆心到直线的距离判断直线与圆的位置关系,这就是曲线
的参数方程为普通方程,然后利用圆心到直线的距离判断直线与圆的位置关系,这就是曲线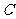 上到直线
上到直线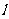 距离为
距离为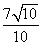 ,然后再判断知
,然后再判断知 ,进而得出结论.
,进而得出结论. 

 w_w w. k#s5_
w_w w. k#s5_
5.(2010湖南理数)3、极坐标方程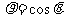 和参数方程
和参数方程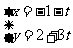 (
( 为参数)所表示的图形分别是
为参数)所表示的图形分别是

 w_w w. k#s5_
w_w w. k#s5_
A、圆、直线 B、直线、圆
C、圆、圆 D、直线、直线

4.(2010湖南理数)5、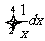 等于
等于

 w_w w. k#s5_
w_w w. k#s5_
A、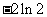 B、
B、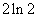 C、
C、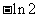 D、
D、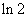

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com