
题目列表(包括答案和解析)
(四)巩固练习:某工厂生产总值月平均增长率为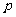 ,则年平均增长率为( )
,则年平均增长率为( )
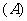
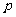
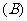
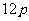
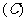
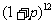
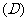

(三)例题分析:
例1.某地区森林原有木材存量为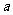 ,且每年增长率为25%,因生产建设的需要每年年底要砍伐的木材量为
,且每年增长率为25%,因生产建设的需要每年年底要砍伐的木材量为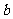 ,设
,设 为
为 年后该地区森林木材的存量,
年后该地区森林木材的存量,
(1)求 的表达式;
的表达式;
(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量不少于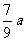 ,如果
,如果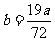 ,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:
,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据: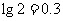 )
)
解:(1)设第一年的森林的木材存量为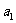 ,第
,第 年后的森林的木材存量为
年后的森林的木材存量为 ,则
,则
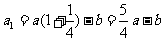 ,
,
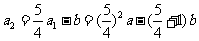 ,
,
 ,
,
………
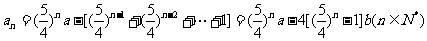 .
.
(2)当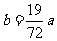 时,有
时,有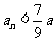 得
得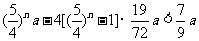 即
即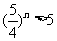 ,
,
所以,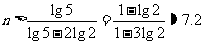 .
.
答:经过8年后该地区就开始水土流失.
例2.轻纺城的一家私营企业主,一月初向银行贷款一万元作开店资金,每月月底获得的利润是该月月初投入资金的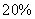 ,每月月底需要交纳房租和所得税为该月所得金额(包括利润)的
,每月月底需要交纳房租和所得税为该月所得金额(包括利润)的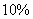 ,每月的生活费开支300元,余款作为资金全部投入再经营,如此继续,问该年年底,该私营企业主有现款多少元?如果银行贷款的年利率为
,每月的生活费开支300元,余款作为资金全部投入再经营,如此继续,问该年年底,该私营企业主有现款多少元?如果银行贷款的年利率为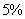 ,问私营企业主还清银行贷款后纯收入还有多少元?
,问私营企业主还清银行贷款后纯收入还有多少元?
解:第一个月月底余
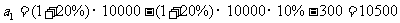 元,
元,
设第 个月月底余
个月月底余 ,第
,第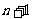 个月月底余
个月月底余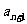 ,
,
则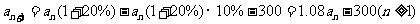 ,
,
从而有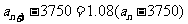 ,
,
设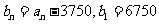 ,∴
,∴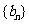 是等比数列
是等比数列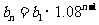 ,
,
∴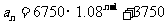 ,
,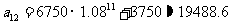 ,
,
还贷后纯收入为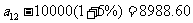 元.
元.
例3.银行按规定每经过一定的时间结算存(贷)款的利息一次,结算后即将利息并入本金,这种计算利息的方法叫做复利.现在有某企业进行技术改造,有两种方案:
甲方案:一次性贷款10万元,第一年便可获得利润1万元,以后每年比上年增加30%的利润;
乙方案:每年贷款1万元,第一年可获得利润1万元,以后每年比前一年多获利5000元.
两种方案的期限都是10年,到期一次行归还本息.若银行贷款利息均以年息10%的复利计算,试比较两个方案哪个获得存利润更多?(计算精确到千元,参考数据: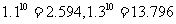 )
)
解:甲方案10年获利润是每年利润数组成的数列的前10项的和:
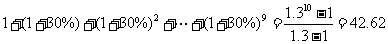 (万元)
(万元)
到期时银行的本息和为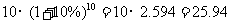 (万元)
(万元)
∴甲方案扣除本息后的净获利为: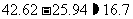 (万元)
(万元)
乙方案:逐年获利成等差数列,前10年共获利:
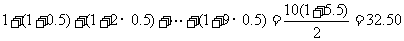 (万元)
(万元)
贷款的本利和为: (万元)
(万元)
∴乙方案扣除本息后的净获利为: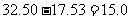 (万元)
(万元)
所以,甲方案的获利较多.
例4.某工厂在1999年的“减员增效”中对部分人员实行分流,规定分流人员第一年可以到原单位领取工资的100%,从第二年起,以后每年只能在原单位按上一年的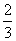 领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得
领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得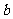 元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流前工资的收入每年
元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流前工资的收入每年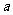 元,分流后进入新经济实体,第
元,分流后进入新经济实体,第 年的收入为
年的收入为 元,
元,
(1)求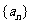 的通项公式;
的通项公式;
(2)当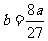 时,这个人哪一年的收入最少?最少为多少?
时,这个人哪一年的收入最少?最少为多少?
(3)当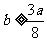 时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
解:(1)由题意得,当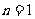 时,
时,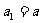 ,当
,当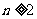 时,
时,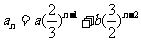 ,
,
∴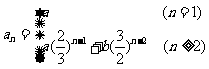 .
.
(2)由已知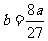 ,
,
当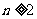 时,
时,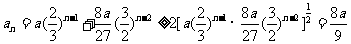 要使得上式等号成立,当且仅当
要使得上式等号成立,当且仅当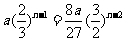 ,即
,即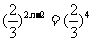 ,解得
,解得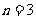 ,因此这个人第三年收入最少为
,因此这个人第三年收入最少为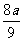 元.
元.
(3)当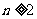 时,
时,
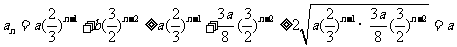 ,上述等号成立,须
,上述等号成立,须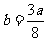 且
且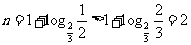 因此等号不能取到,
因此等号不能取到,
当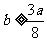 时,这个人分流一年后的收入永远超过分流前的年收入.
时,这个人分流一年后的收入永远超过分流前的年收入.
(二)主要方法:
1.解答数列应用题要注意步骤的规范性:设数列,判断数列,解题完毕要作答;
2.在归纳或求通项公式时,一定要将项数 计算准确;
计算准确;
3.在数列类型不易分辨时,要注意归纳递推关系;
4.在近似计算时,要注意应用对数方法和二项式定理,且要看清题中对近似程度的要求.
(一)主要知识:
1.解应用问题的核心是建立数学模型;
2.一般步骤:审题、抓住数量关系、建立数学模型;
3.注意问题是求什么(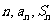 ).
).
2.能够把实际问题转化成数列问题.
19.设数列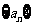 和
和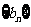 满足
满足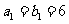 ,
,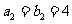 ,
,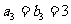 ,且数列
,且数列

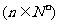 是等差数列,数列
是等差数列,数列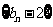
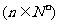 是等比数列。
是等比数列。
(Ⅰ)求数列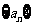 和
和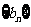 的通项公式;
的通项公式;
(Ⅱ)是否存在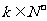 ,使
,使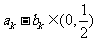 ?若存在,求出
?若存在,求出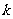 的值;若不存在,说明理由。
的值;若不存在,说明理由。
|

|
版权所有:()
版权所有:()
18.已知 在
在 上是增函数,而且
上是增函数,而且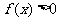 ,
,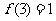 。判断
。判断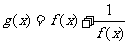
在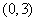 上是增函数还是减函数,并加以证明。
上是增函数还是减函数,并加以证明。
解:函数g(x)在 (0,3)上是减函数. 证明如下:任取0<x1<x2≤3,
则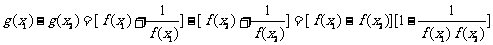 .
.
∵f(x)在(0,+∞)是增函数,∴f(x1)-f(x2)<0. 又f(x)>0,f(3)=1,
∴0<f(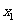 )<f(
)<f(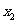 )≤f(3)=1,
)≤f(3)=1,
∴0<f(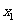 )·f(
)·f(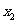 )<1,
)<1,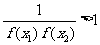 ,
, .
.
∴g(x1)- g(x2)>0,即g(x1) >g(x2)
由此可知,函数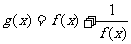 在(0,3)上是减函数。
在(0,3)上是减函数。
17.已知: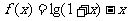 在
在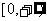 上是减函数,解关于
上是减函数,解关于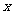 的不等式
的不等式
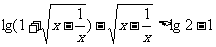 .
.
解:由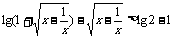 ,得
,得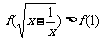 .
.

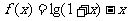 在
在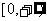 上是减函数,
上是减函数, 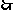
 ,这等价于
,这等价于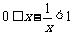 ,
,
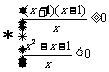 ,解之得
,解之得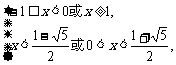
故不等式的解为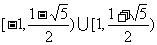 .
.
16.数列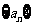 中,
中,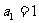 ,当
,当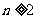 时,其前
时,其前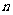 项和
项和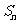 满足
满足 。
。
(Ⅰ)求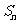 的表达式;
的表达式;
(Ⅱ)设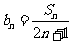 ,数列
,数列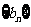 的前
的前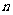 项和为
项和为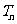 ,求
,求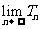 。
。
15.已知数列|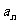 |满足
|满足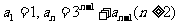
(I)求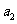 ,
,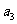 ;
;
(II)证明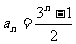 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com