
题目列表(包括答案和解析)
(二)主要方法:
1.求函数解析式的题型有:
(1)已知函数类型,求函数的解析式:待定系数法;
(2)已知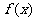 求
求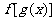 或已知
或已知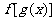 求
求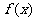 :换元法、配凑法;
:换元法、配凑法;
(3)已知函数图像,求函数解析式;
(4)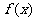 满足某个等式,这个等式除
满足某个等式,这个等式除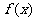 外还有其他未知量,需构造另个等式:解方程组法;
外还有其他未知量,需构造另个等式:解方程组法;
(5)应用题求函数解析式常用方法有待定系数法等.
2.求函数定义域一般有三类问题:
(1)给出函数解析式的:函数的定义域是使解析式有意义的自变量的取值集合;
(2)实际问题:函数的定义域的求解除要考虑解析式有意义外,还应考虑使实际问题有意义;
(3)已知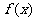 的定义域求
的定义域求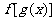 的定义域或已知
的定义域或已知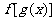 的定义域求
的定义域求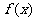 的定义域:
的定义域:
①掌握基本初等函数(尤其是分式函数、无理函数、对数函数、三角函数)的定义域;
②若已知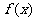 的定义域
的定义域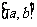 ,其复合函数
,其复合函数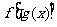 的定义域应由
的定义域应由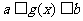 解出.
解出.
(一)主要知识:1.函数解析式的求解;2.函数定义域的求解.
|

|
版权所有:()
版权所有:()
(四)巩固练习:设数列 的前
的前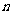 项和为
项和为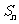 ,则
,则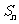 等于( )
等于( )





(三)例题分析:
例1.求下列数列的前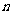 项和
项和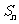 :
:
(1)5,55,555,5555,…,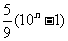 ,…; (2)
,…; (2)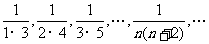 ;
;
(3)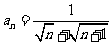 ;
(4)
;
(4) ;
;
(5)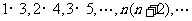 ;(6)
;(6)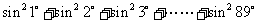 .
.
解:(1)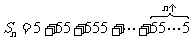

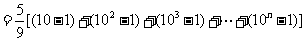
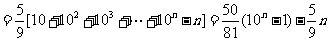 .
.
(2)∵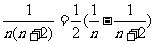 ,
,
∴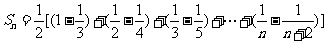
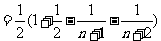 .
.
(3)∵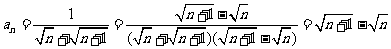
∴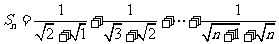
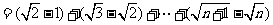
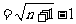 .
.
(4)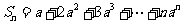 ,
,
当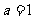 时,
时, …
… ,
,
当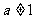 时,
时,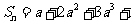 …
…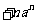 ,
,
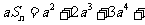 …
…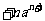 ,
,
两式相减得 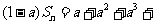 …
…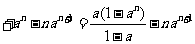 ,
,
∴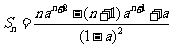 .
.
(5)∵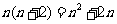 ,
,
∴ 原式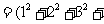 …
…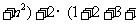 …
…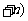
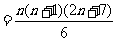 .
.
(6)设 ,
,
又∵ ,
,
∴ 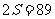 ,
, .
.
例2.已知数列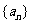 的通项
的通项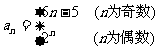 ,求其前
,求其前 项和
项和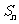 .
.
解:奇数项组成以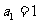 为首项,公差为12的等差数列,
为首项,公差为12的等差数列,
偶数项组成以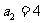 为首项,公比为4的等比数列;
为首项,公比为4的等比数列;
当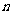 为奇数时,奇数项有
为奇数时,奇数项有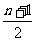 项,偶数项有
项,偶数项有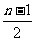 项,
项,
∴ ,
,
当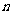 为偶数时,奇数项和偶数项分别有
为偶数时,奇数项和偶数项分别有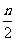 项,
项,
∴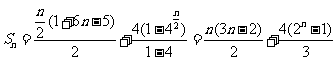 ,
,
所以,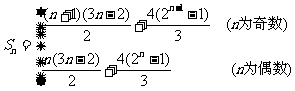 .
.
例3.(《高考A计划》智能训练14题)数列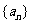 的前
的前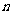 项和
项和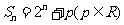 ,数列
,数列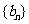 满足
满足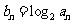 ,若
,若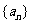 是等比数列,
是等比数列,
(1) 求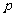 的值及通项
的值及通项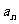 ;
;
(2)求和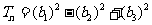 …
…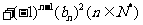 .
.
(解答见教师用书127页)
(二)主要方法:
1.求数列的和注意方法的选取:关键是看数列的通项公式;
2.求和过程中注意分类讨论思想的运用;
3.转化思想的运用;
(一)主要知识:
1.等差数列与等比数列的求和公式的应用;
2.倒序相加、错位相减,分组求和、拆项求和等求和方法;
3.熟记一些常用的数列的和的公式.
2.能运用倒序相加、错位相减、拆项相消等重要的数学方法进行求和运算;
|

|
版权所有:()
版权所有:()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com