
题目列表(包括答案和解析)
(一)主要知识:函数的综合问题主要有如下几个方面:
1.函数的概念、性质和方法的综合问题;
2.函数与其它知识,如方程、不等式、数列的综合问题;
3.函数与解析几何的综合问题;
4.联系生活实际和生产实际的应用问题.
(三)例题分析:
例1.设全集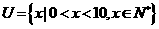 ,若
,若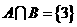 ,
,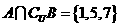 ,
,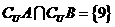 ,则
,则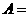
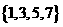 ,
,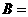
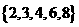 .
.
解法要点:利用文氏图.
例2.已知集合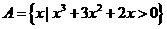 ,
,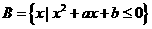 ,若
,若
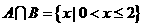 ,
,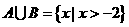 ,求实数
,求实数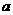 、
、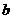 的值.
的值.
解:由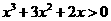 得
得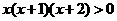 ,∴
,∴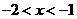 或
或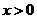 ,
,
∴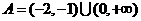 ,又∵
,又∵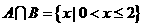 ,且
,且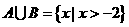 ,
,
∴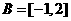 ,∴
,∴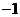 和
和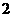 是方程
是方程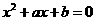 的根,
的根,
由韦达定理得: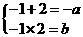 ,∴
,∴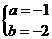 .
.
说明:区间的交、并、补问题,要重视数轴的运用.
例3.已知集合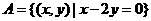 ,
,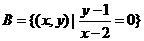 ,则
,则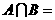
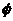 ;
;
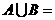
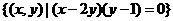 ;(参见《高考
;(参见《高考 计划》考点2“智能训练”第6题).
计划》考点2“智能训练”第6题).
解法要点:作图.
注意:化简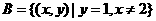 ,
,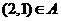 .
.
例4.(《高考 计划》考点2“智能训练”第15题)已知集合
计划》考点2“智能训练”第15题)已知集合
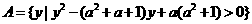 ,
,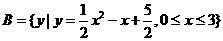 ,
,
若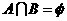 ,求实数
,求实数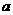 的取值范围.
的取值范围.
解答见教师用书第9页.
例5.(《高考 计划》考点2“智能训练”第16题)已知集合
计划》考点2“智能训练”第16题)已知集合
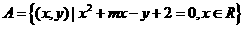 ,
,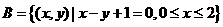 ,
,
若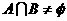 ,求实数
,求实数 的取值范围.
的取值范围.
分析:本题的几何背景是:抛物线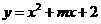 与线段
与线段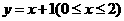 有公共点,求实数
有公共点,求实数 的取值范围.
的取值范围.
解法一:由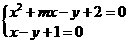 得
得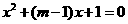 ①
①
∵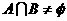 ,∴方程①在区间
,∴方程①在区间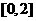 上至少有一个实数解,
上至少有一个实数解,
首先,由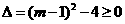 ,解得:
,解得: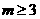 或
或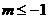 .
.
设方程①的两个根为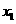 、
、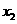 ,
,
(1)当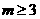 时,由
时,由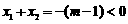 及
及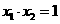 知
知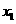 、
、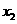 都是负数,不合题意;
都是负数,不合题意;
(2)当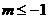 时,由
时,由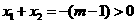 及
及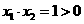 知
知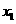 、
、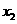 是互为倒数的两个正数,
是互为倒数的两个正数,
故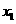 、
、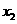 必有一个在区间
必有一个在区间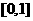 内,从而知方程①在区间
内,从而知方程①在区间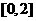 上至少有一个实数解,
上至少有一个实数解,
综上所述,实数 的取值范围为
的取值范围为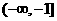 .
.
解法二:问题等价于方程组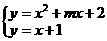 在
在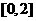 上有解,
上有解,
即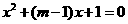 在
在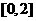 上有解,
上有解,
令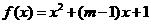 ,则由
,则由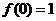 知抛物线
知抛物线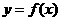 过点
过点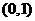 ,
,
∴抛物线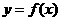 在
在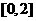 上与
上与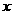 轴有交点等价于
轴有交点等价于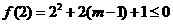 ①
①
或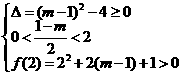 ②
②
由①得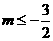 ,由②得
,由②得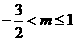 ,
,
∴实数 的取值范围为
的取值范围为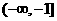 .
.
(二)主要方法:
1.求交集、并集、补集,要充分发挥数轴或文氏图的作用;
2.含参数的问题,要有讨论的意识,分类讨论时要防止在空集上出问题;
3.集合的化简是实施运算的前提,等价转化常是顺利解题的关键.
(一)主要知识:
1.交集、并集、全集、补集的概念;
2.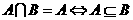 ,
,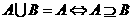 ;
;
3.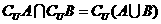 ,
,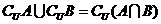 .
.
15.已知二次函数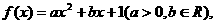 方程
方程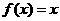 有两个实数根
有两个实数根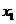 、
、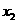 。
。
(Ⅰ)如果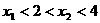 ,设函数
,设函数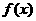 的对称轴为
的对称轴为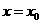 ,求证
,求证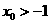 ;
;
(Ⅱ)如果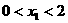 ,且
,且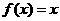 的两实根相差为2,求实数
的两实根相差为2,求实数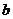 的取值范围。
的取值范围。
|

|
版权所有:()
版权所有:()
15.运输一批海鲜,可在汽车、火车、飞机三种运输工具中选择.它们的速度分别为50千米/小时,100千米/小时,500千米/小时,每千米的运费分别为a元、b元、c元,且b<a<c. 又这批海鲜在运输过程中的损耗为500元/小时,若使用三种运输工具分别运输时各自的总费用(运费与损耗之和)互不相等,试确定使用哪种运输工具总费用最省.(题中字母均为正的已知量)
14.设函数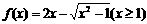
(Ⅰ)解不等式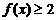 ;
;
(Ⅱ)求出最大的实数a,使得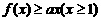 恒成立.
恒成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com