
题目列表(包括答案和解析)
(三)例题分析:
例1.求函数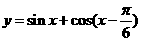 的最大值和最小值.
的最大值和最小值.
解: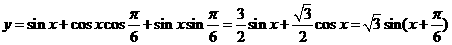 .
.
当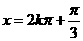 ,
,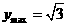 ,当
,当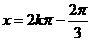 ,
,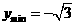
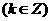 .
.
例2.求函数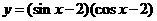 的最大、最小值.
的最大、最小值.
解:原函数可化为: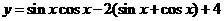 ,
,
令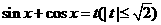 ,
,
则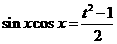 ,∴
,∴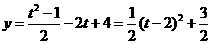 .
.
∵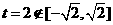 ,且函数在
,且函数在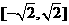 上为减函数,∴当
上为减函数,∴当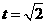 时,即
时,即 时,
时,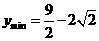 ;当
;当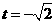 时,即
时,即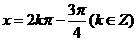 时,
时,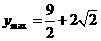 .
.
例3.求下列各式的最值:
(1)已知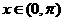 ,求函数
,求函数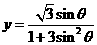 的最大值;
的最大值;
(2)已知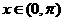 ,求函数
,求函数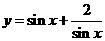 的最小值.
的最小值.
解:(1)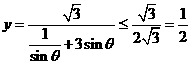 ,当且仅当
,当且仅当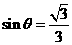 时等号成立.
时等号成立.
故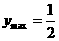 .
.
(2)设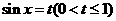 ,则原函数可化为
,则原函数可化为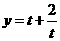 ,在
,在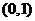 上为减函数,∴当
上为减函数,∴当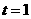 时,
时,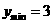 .
.
说明: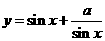 型三角函数求最值,当
型三角函数求最值,当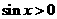 ,
,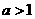 时,不能用均值不等式求最值,适宜用函数在区间内的单调性求解.
时,不能用均值不等式求最值,适宜用函数在区间内的单调性求解.
例4.求函数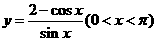 的最小值.
的最小值.
解:原式可化为
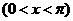 ,引入辅助角
,引入辅助角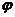 ,
,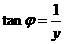 ,得
,得
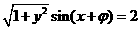 ,∴
,∴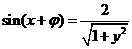 ,由
,由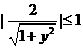 ,
,
得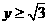 或
或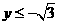 .
.
又∵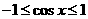 ,∴
,∴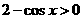 ,且
,且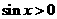 ,故
,故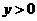 .∴
.∴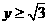 ,故
,故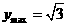 .
.
例5.《高考 计划》考点32,智能训练10:已知
计划》考点32,智能训练10:已知 ,则
,则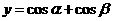 的最大值是
.
的最大值是
.
解:∵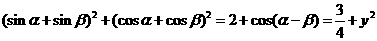 ,
,
∴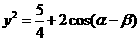 ,故当
,故当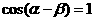 时,
时,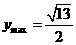 .
.
(二)主要方法:①配方法;②化为一个角的三角函数;③数形结合法;④换元法;⑤基本不等式法.
(一)主要知识:求三角函数的最值,主要利用正、余弦函数的有界性,一般通过三角变换化为下列基本类型处理:
①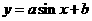 ,设
,设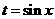 化为一次函数
化为一次函数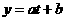 在闭区间
在闭区间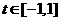 上的最值求之;
上的最值求之;
② ,引入辅助角
,引入辅助角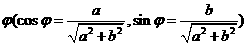 ,化为
,化为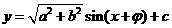 求解方法同类型①;
求解方法同类型①;
③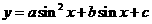 ,设
,设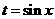 ,化为二次函数
,化为二次函数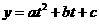 在
在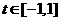 上的最值求之;
上的最值求之;
④ ,设
,设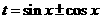 化为二次函数
化为二次函数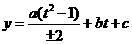 在闭区间
在闭区间 上的最值求之;
上的最值求之;
⑤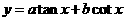 ,设
,设 化为
化为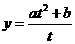 用
用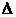 法求值;当
法求值;当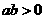 时,还可用平均值定理求最值;
时,还可用平均值定理求最值;
⑥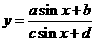 根据正弦函数的有界性,即可分析法求最值,还可“不等式”法或“数形结合”.
根据正弦函数的有界性,即可分析法求最值,还可“不等式”法或“数形结合”.
18.已知一个数列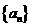 的各项是
的各项是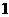 或
或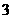 .首项为
.首项为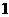 ,且在第
,且在第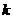 个
个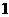 和第
和第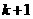 个
个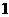 之间有
之间有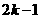 个
个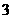 ,即
,即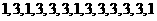 ,….记数列的前
,….记数列的前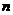 项的和为
项的和为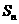 .
.
(Ⅰ)试问第 个
个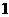 为该数列的第几项?
为该数列的第几项?
(Ⅱ)求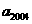 ;
;
(Ⅲ) ;
;
(Ⅳ)是否存在正整数 ,使得
,使得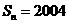 ?如果存在,求出
?如果存在,求出 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
解:将第k个1与第k+1个1前的3记为第k对,即(1,3)为第1对,共1+1=2项;(1,3,3,3)为第2对,共1+(2×2-1)=4项;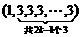 为第k对,共1+(2k-1)=2k项;….故前k对共有项数为2+4+6+…+2k=k(k+1).
为第k对,共1+(2k-1)=2k项;….故前k对共有项数为2+4+6+…+2k=k(k+1).
(Ⅰ)第2004个1所在的项为前2003对所在全部项的后1项,即为2003(2003+1)+1=4014013(项).
(Ⅱ)因44×45=1980,45×46=2070,故第2004项在第45对内,从而a2004=3.
(Ⅲ)由(Ⅱ)可知,前2004项中共有45个1,其余1959个数均为3,于是S2004=45+3×1959=5922.
(Ⅳ)前k对所在全部项的和为 Sk(k+1)=k+3[k(k+1)-k]=3k2+k.
易得,S25(25+1)=3×252+25=1900,S26(26+1)=3×262+26=2054,S651=1901,且自第652项到第702项均为3,而2004-1901=103不能被3整除,故不存在m,使Sm=2004.
已知集合M是满足下列性质的函数f(x)的全体:存在非零常数k,对任意x∈D(D为函数的定义域),等式f(kx)=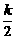 +f(x)成立.
+f(x)成立.
(Ⅰ)一次函数f(x)= ax+b(a≠0)是否属于集合M?说明理由;
(Ⅱ)设函数f(x)=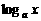 (a>1)的图象与y=x的图象有公共点,试证明:
(a>1)的图象与y=x的图象有公共点,试证明:
f(x)=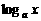 ∈M.
∈M.
 (Ⅰ)若一次函数f(x)∈M,即存在非零常数k,使得等式akx+b=
(Ⅰ)若一次函数f(x)∈M,即存在非零常数k,使得等式akx+b=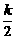 + ax+b,也就是a(k-1)x=
+ ax+b,也就是a(k-1)x=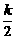 成立.显然对于任意x∈D=R,a(k-1)x=
成立.显然对于任意x∈D=R,a(k-1)x=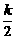 不能恒成立,故f(x)= ax+bÏM.
不能恒成立,故f(x)= ax+bÏM.
(Ⅱ)如图,设函数f(x)=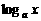 (a>1)的图象与函数y=x的图象的公共点为B(t,t),则显然t>1.在x∈(1,t)上,函数f(x)=
(a>1)的图象与函数y=x的图象的公共点为B(t,t),则显然t>1.在x∈(1,t)上,函数f(x)=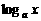 (a>1)有定义,故在函数f(x)=
(a>1)有定义,故在函数f(x)=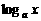 (a>1,x∈(1,t))的图象即弧AB上,必存在点C(k,
(a>1,x∈(1,t))的图象即弧AB上,必存在点C(k,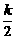 ),使等式
),使等式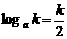 成立,其中1<k<t.
成立,其中1<k<t.
于是,f(kx)=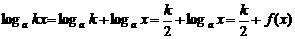 ,故f(x)=
,故f(x)=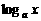 ∈M.
∈M.
|

|
版权所有:()
版权所有:()
17.(本小题满分10分)对于函数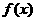 ,若存在
,若存在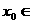 R,使
R,使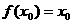 成立,则称
成立,则称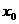 为
为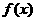 的不动点,如果函数
的不动点,如果函数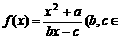
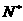 )有且只有两个不动点
)有且只有两个不动点 ,
,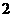 ,且
,且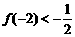 .
.
(1)求函数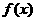 的解析式;
的解析式;
(2)已知各项不为零的数列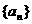 满足
满足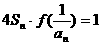 ,求数列通项
,求数列通项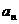 ;
;
(3)如果数列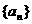 满足
满足 ,求证当
,求证当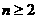 时,恒有
时,恒有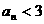 成立.
成立.
解:(1)设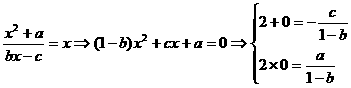
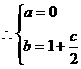
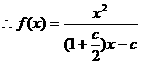 2分
2分
由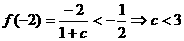
又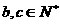 ,
,  4分
4分
(2)由已知
相减得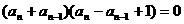 6分
6分
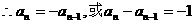
当n=1时,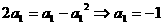 ,若
,若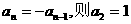
这与 矛盾,
矛盾,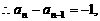
 9分
9分
(3)由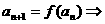
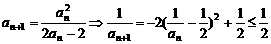 ,
,
 11分
11分
若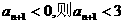 成立;
成立;
若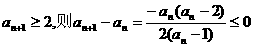
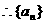 在
在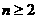 时单调递减.
时单调递减.
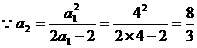 ,可知
,可知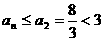 ,在
,在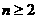 时成立14分
时成立14分
16.(本小题满分8分)已知锐角三角形 中,
中,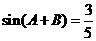 ,
,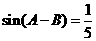 。
。
(Ⅰ)求证: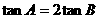 ;
;
(Ⅱ)设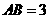 ,求
,求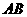 边上的高。
边上的高。
(Ⅰ)证明:

所以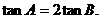
(Ⅱ)解: ,
,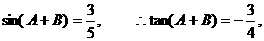
即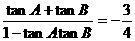 ,将
,将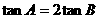 代入上式并整理得
代入上式并整理得

解得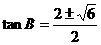 ,舍去负值得
,舍去负值得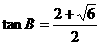 ,
,
 设AB边上的高为CD.
设AB边上的高为CD.
则AB=AD+DB=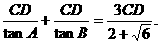
由AB=3,得CD=2+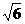 . 所以AB边上的高等于2+
. 所以AB边上的高等于2+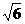 .
.
15.(本小题满分8分)已知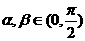 且满足
且满足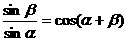 .
.
(1)求证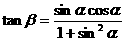 ;
;
(2)求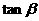 的最大值,并求当
的最大值,并求当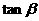 取得最大值时,
取得最大值时,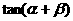 的值.
的值.
解:(1)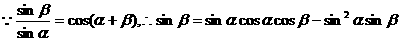 2分
2分
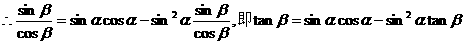 4分
4分
 5分
5分
(2)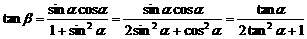 7分
7分
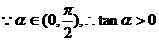
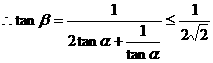 9分
9分
当且仅当 取最大值,最大值为
取最大值,最大值为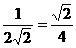
此时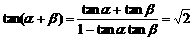 12分
12分
14.某品牌彩电为了打开市场,促进销售,准备对某特定型号的彩电降价,现有四种降价方案:
方案①:先降价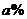 ,再降价
,再降价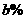 ;
;
方案②:先降价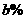 ,再降价
,再降价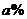 ;
;
方案③:先降价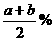 ,再降价
,再降价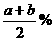 ;
;
方案④:一次性降价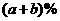 。
。
其中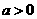 ,
,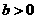 ,且
,且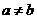 。
。
上述四种方案中,降价幅度最小的是方案________③_____________.
13.如果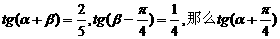 的值是
的值是 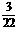 .
.
12.设正数数列{an}前n项和为Sn,且存在正数t,使得对所有自然数n,有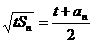 ,则通过归纳猜测可得到Sn= n2t .
,则通过归纳猜测可得到Sn= n2t .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com