
题目列表(包括答案和解析)
(三)例题分析:
例1.化简:
(1) ;
;
(2)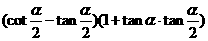 ;
;
(3) .
.
解:(1)原式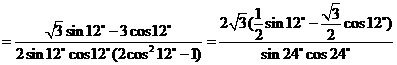
 .
.
(2)原式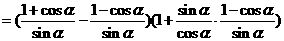
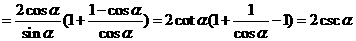 .
.
(3)原式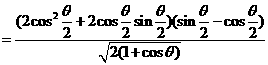

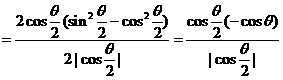
∵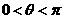 ,∴
,∴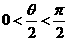 ,∴
,∴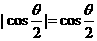 ,
,
∴原式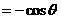 .
.
例3.证明:(1)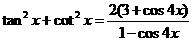 ;
;
(2)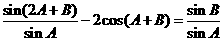 .
.
证:(1)左边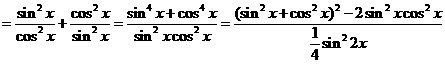
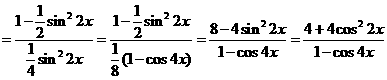
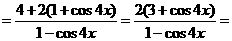 右边,∴得证.
右边,∴得证.
说明:由等式两边的差异知:若选择“从左证到右”,必定要“切化弦”;若“从右证到左”,必定要用倍角公式.
(2)左边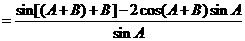
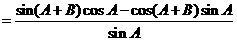
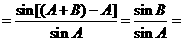 右边,∴得证.
右边,∴得证.
(二)主要方法:
1.三角函数式的化简:
三角函数式的化简常用方法是:异名函数化为同名三角函数,异角化为同角,异次化为同次,切割化弦,特殊值与特殊角的三角函数互化.
2.三角恒等式的证明:
三角恒等式包括有条件的恒等式和无条件的恒等式.①无条件的等式证明的基本方法是化繁为简、左右归一、变更命题等,使等式两端的“异”化为“同”;②有条件的等式常用方法有:代入法、消去法、综合法、分析法等.
(一)主要知识:
1.三角函数式的化简要求:通过对三角函数式的恒等变形(或结合给定条件而进行的恒等变形),使最后所得到的结果中:①所含函数和角的名类或种类最少;②各项的次数尽可能地低;③出现的项数最少;④一般应使分母和根号不含三角函数式;⑤对能求出具体数值的,要求出值.
2.三角恒等式的证明要求:利用已知三角公式通过恒等变形(或结合给定条件运用三角公式),论证所给等式左、右相等,要求过程清晰、步骤完整.
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.如果函数 的图象关于直线
的图象关于直线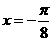 对称,则
对称,则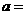
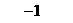 ;
;
2.若函数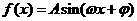 (
(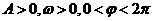 )的最小值为
)的最小值为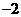 ,周期为
,周期为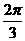 ,且它的图象过点
,且它的图象过点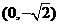 ,求此函数解析式.(
,求此函数解析式.(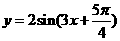 或
或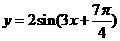 )
)
(三)例题分析:
例1.(1)将函数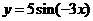 的周期扩大到原来的2倍,再将函数图象左移
的周期扩大到原来的2倍,再将函数图象左移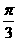 ,得到图象对应解析式是
(
,得到图象对应解析式是
(  )
)
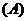
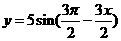
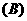
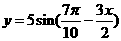

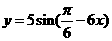
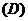

(2)若函数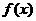 图象上每一个点的纵坐标保持不变,横坐标伸长到原来的两倍,然后再将整个图象沿
图象上每一个点的纵坐标保持不变,横坐标伸长到原来的两倍,然后再将整个图象沿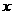 轴向右平移
轴向右平移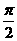 个单位,向下平移3个单位,恰好得到
个单位,向下平移3个单位,恰好得到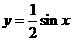 的图象,则
的图象,则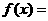
 .
.
(3)先将函数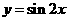 的图象向右平移
的图象向右平移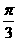 个单位长度,再将所得图象作关于
个单位长度,再将所得图象作关于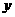 轴的对称变换,则所得函数图象对应解析式为
轴的对称变换,则所得函数图象对应解析式为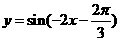 .
.
例2.已知函数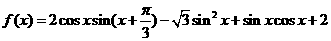 (
( ),该函数的图象可由
),该函数的图象可由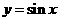 (
( )的图象经过怎样的变换得到?
)的图象经过怎样的变换得到?
解: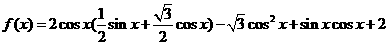

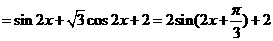
①由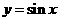 的图象向左平移
的图象向左平移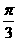 个单位得
个单位得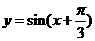 图象,
图象,
②再保持图象上各点纵坐标不变,横坐标变为原来的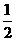 得
得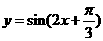 图象,
图象,
③再保持图象上各点横坐标不变,纵坐标变为原来的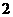 倍得
倍得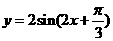 图象,
图象,
④最后将所得图象向上平移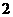 个单位得
个单位得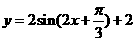 的图象.
的图象.
说明:(1)本题的关键在于化简得到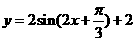 的形式;(2)若在水平方向先伸缩再平移,则要向左平移
的形式;(2)若在水平方向先伸缩再平移,则要向左平移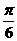 个单位了.
个单位了.
例3.函数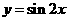 的图象向右平移
的图象向右平移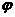 (
(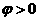 )个单位,得到的图象关于直线
)个单位,得到的图象关于直线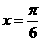 对称,则
对称,则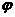 的最小值为
(
的最小值为
(  )
)
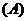
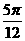
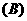
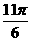

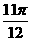
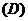 以上都不对
以上都不对
略解:平移后解析式为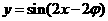 ,图象关于
,图象关于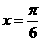 对称,
对称,
∴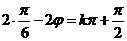 (
(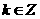 ),∴
),∴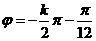 (
(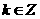 ),∴当
),∴当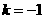 时,
时,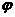 的最小值为
的最小值为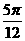 .
.
 例4.已知函数
例4.已知函数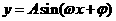 (
(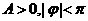 )的一段图象如下图所示,求函数的解析式.
)的一段图象如下图所示,求函数的解析式.
解:由图得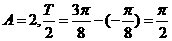 ,∴
,∴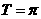 ,∴
,∴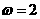 ,
,
∴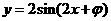 ,又∵图象经过点
,又∵图象经过点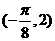 ,
,
∴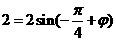 ,∴
,∴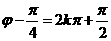 (
(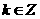 ),
),
∴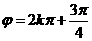 ,∴函数解析式为
,∴函数解析式为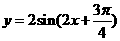 .
.
(二)主要方法:
1.“五点法”画正弦、余弦函数和函数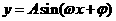 的简图,五个特殊点通常都是取三个平衡点,一个最高、一个最低点;
的简图,五个特殊点通常都是取三个平衡点,一个最高、一个最低点;
2.给出图象求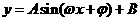 的解析式的难点在于
的解析式的难点在于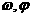 的确定,本质为待定系数法,基本方法是:①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到的,通常可由平衡点或最值点确定周期
的确定,本质为待定系数法,基本方法是:①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到的,通常可由平衡点或最值点确定周期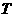 ,进而确定
,进而确定 .
.
(一)主要知识:
1.三角函数线:正弦线、余弦线、正切线的作法;
2.函数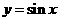 的图象到函数
的图象到函数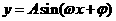 的图象的两种主要途径.
的图象的两种主要途径.
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.函数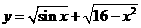 的定义域为
的定义域为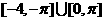 .
.
2.函数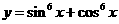 的最小正周期为
的最小正周期为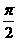 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com