
题目列表(包括答案和解析)
(三)例题分析:
例1.已知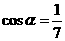 ,
, ,
, ,
,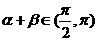 求
求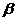 的值.
的值.
解:∵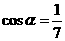 ,
, ,∴
,∴ ,
,
又∵ ,
,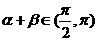 ,∴
,∴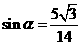 ,
,
∵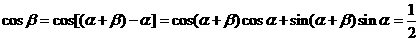 ,
,
又∵ ,
,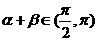 ,
,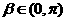 ∴
∴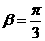 .
.
例2.已知 为一三角形的內角,求
为一三角形的內角,求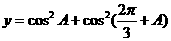 的取值范围.
的取值范围.
解: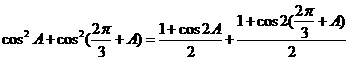
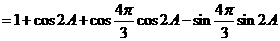
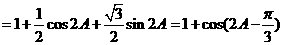 .
.
∵ 为一三角形內角,
为一三角形內角, ,
,
∴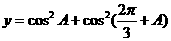 的取值范围是
的取值范围是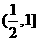 .
.
例3.求值: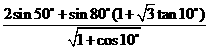 .
.
解:原式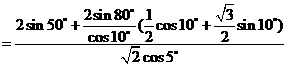
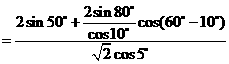
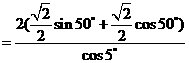
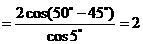 .
.
例4.是否存在两个锐角 满足(1)
满足(1)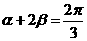 ;(2)
;(2)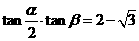 同时成立,若存在,求出
同时成立,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
解:由(1)得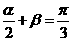 ,∴
,∴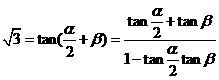 ,
,
∴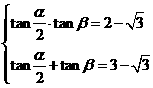 ,∴
,∴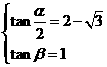 或
或 (∵
(∵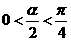 ,∴
,∴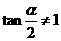 ,舍去),
,舍去),
∴ 为所求满足条件的两个锐角.
为所求满足条件的两个锐角.
(二)主要方法:
1.寻求所求结论中的角与已知条件中的角的关系,把握式子的变形方向,准确运用公式;
2.三角变换主要体现在:函数名称的变换、角的变换、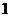 的变换、和积的变换、幂的变换等方面;
的变换、和积的变换、幂的变换等方面;
3.掌握基本技巧:切割化弦,异名化同名,异角化同角等.
(一)主要知识:
1.两角和与差的三角函数公式;二倍角公式;
2.降次公式: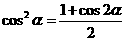 ,
,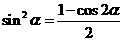 .
.
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.若 ,则
,则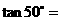 (
(  )
)
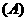
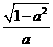
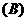
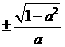

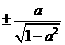

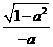
2.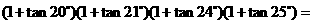 (
(  )
)
 2
2  4
4  8
8  16
16
(三)例题分析:
例1.已知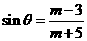 ,
,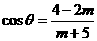 (
(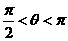 ),则
),则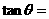 (
( 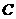 )
)
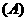
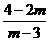
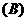
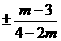

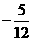

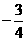 或
或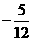
略解:由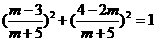 得
得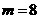 或
或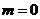 (舍),∴
(舍),∴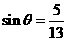 ,
,
∴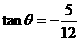 .
.
例2.已知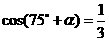 ,
,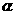 是第三象限角,求
是第三象限角,求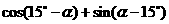 的值.
的值.
解:∵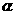 是第三象限角,∴
是第三象限角,∴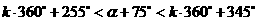 (
(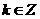 ),
),
∵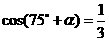 ,∴
,∴ 是第四象限角,
是第四象限角,
∴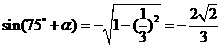 ,
,
∴原式 .
.
例3.已知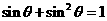 ,求
,求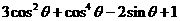 的值.
的值.
解:由题意, ,
,
∴原式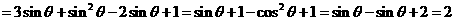 .
.
例4.已知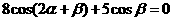 ,求
,求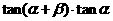 的值.
的值.
解:∵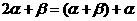 ,
,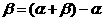 ,
,
∴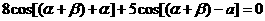 ,
,
得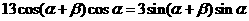 ,若
,若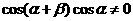 ,则
,则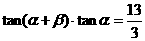 ,
,
若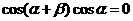 ,
,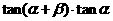 无意义.
无意义.
说明:角的和、差、倍、半具有相对性,如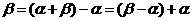 ,
,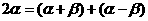 ,
,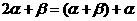 等,解题过程中应充分利用这种变形.
等,解题过程中应充分利用这种变形.
例5.已知关于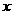 的方程
的方程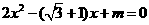 的两根为
的两根为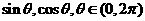 ,
,
求:(1)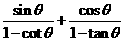 的值;(2)
的值;(2) 的值;(3)方程的两根及此时
的值;(3)方程的两根及此时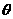 的值.
的值.
|
|
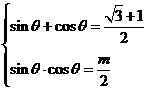 ,
,
∴原式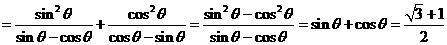 .
.
(2)由①平方得: ,
,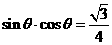 ,即
,即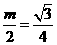 ,故
,故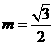 .
.
(3)当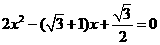 ,解得
,解得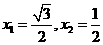 ,
,
∴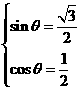 或
或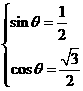 , ∵
, ∵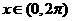 ,∴
,∴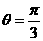 或
或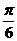 .
.
(二)主要方法:
1.寻求角与角之间的关系,化非特殊角为特殊角;
2.正确灵活地运用公式,通过三角变换消去或约去一些非特殊角的三角函数值;
3.一些常规技巧:“1”的代换、切割化弦、和积互化、异角化同角等.
(一)主要知识:
三角函数求值问题一般有三种基本类型:
1.给角求值,即在不查表的前提下,求三角函数式的值;
2.给值求值,即给出一些三角函数,而求与这些三角函数式有某种联系的三角式的值;
3.给值求角,即给出三角函数值,求符合条件的角.
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.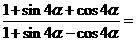 (
( 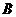 )
)
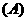

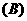


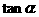
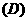
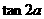
2.已知 ,当
,当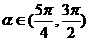 时,式子
时,式子 可化简(
可化简(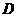 )
)
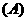

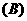



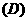
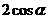
3.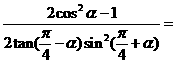 1 .
1 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com