
题目列表(包括答案和解析)
3.一个平面把空间分成__2__部分,两个平面把空间最多分成_4___部分,三个平面把空间最多分成__8__部分.
2.有下列命题:
①空间四点中有三点共线,则这四点必共面;②空间四点中,其中任何三点不共线,则这四点不共面;③用斜二测画法可得梯形的直观图仍为梯形;④垂直于同一直线的两直线平行⑤两组对边相等的四边形是平行四边形.
其中正确的命题是 .
答案:①③
1.在空间四边形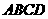 的边
的边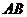 、
、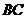 、
、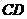 、
、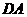 上分别取点
上分别取点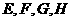 ,如果
,如果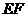 与
与 相交于一点
相交于一点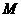 ,那么
(
,那么
(  )
)
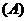
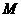 一定在直线
一定在直线 上
上 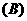
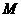 一定在直线
一定在直线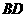 上
上

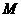 可能在直线
可能在直线 上,也可能在直线
上,也可能在直线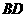 上
上
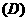
 既不在直线
既不在直线 上,也不在直线
上,也不在直线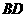 上
上
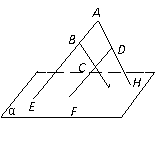 例1.如图,在四边形ABCD中,已知AB∥CD,直线AB,BC,AD,DC分别与平面α相交于点E,G,H,F.求证:E,F,G,H四点必定共线.
例1.如图,在四边形ABCD中,已知AB∥CD,直线AB,BC,AD,DC分别与平面α相交于点E,G,H,F.求证:E,F,G,H四点必定共线.
解:∵AB∥CD,
∴AB,CD确定一个平面β.
又∵AB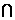 α=E,AB
α=E,AB β,∴E∈α,E∈β,
β,∴E∈α,E∈β,
即E为平面α与β的一个公共点.
同理可证F,G,H均为平面α与β的公共点.
∵两个平面有公共点,它们有且只有一条通过公共点的公共直线,
∴E,F,G,H四点必定共线.
说明:在立体几何的问题中,证明若干点共线时,常运用公理2,即先证明这些点都是某二平面的公共点,而后得出这些点都在二平面的交线上的结论.
例2.已知:a,b,c,d是不共点且两两相交的四条直线,求证:a,b,c,d共面.
证明 1o若当四条直线中有三条相交于一点,不妨设a,b,c相交于一点A,
但AÏd,如图1.
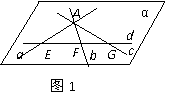 ∴直线d和A确定一个平面α.
∴直线d和A确定一个平面α.
又设直线d与a,b,c分别相交于E,F,G,
则A,E,F,G∈α.
∵A,E∈α,A,E∈a,∴a α.
α.
同理可证b α,c
α,c α.
α.
∴a,b,c,d在同一平面α内.
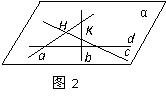 2o当四条直线中任何三条都不共点时,如图2.
2o当四条直线中任何三条都不共点时,如图2.
∵这四条直线两两相交,则设相交直线a,b确定一个平面α.
设直线c与a,b分别交于点H,K,则H,K∈α.
又 H,K∈c,∴c,则c α.
α.
同理可证d α.
α.
∴a,b,c,d四条直线在同一平面α内.
说明:证明若干条线(或若干个点)共面的一般步骤是:首先根据公理3或推论,由题给条件中的部分线(或点)确定一个平面,然后再根据公理1证明其余的线(或点)均在这个平面内.本题最容易忽视“三线共点”这一种情况.因此,在分析题意时,应仔细推敲问题中每一句话的含义.
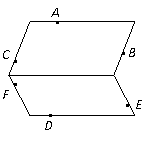
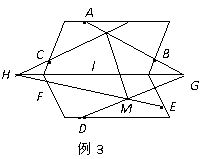
例3.如图,点A,B,C确定的平面与点D,E,F确定的平面相交于直线l,且直线AB与l相交于点G,直线EF与l相交于点H,试作出平面ABD与平面CEF的交线.
解:如图3,在平面ABC内,连结AB,与l相交于点G,则G∈平面DEF;在平面DEF内,连结DG,与EF相交于点M,则M∈平面ABD,且M∈平面CEF.所以,M在平面ABD与平面CEF的交线上.同理,可作出点N,N在平面ABD与平面CEF的交线上.连结MN,直线MN即为所求.
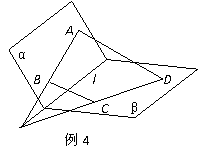
例4.如图,已知平面α,β,且α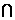 β=l.设梯形ABCD中,AD∥BC,且AB
β=l.设梯形ABCD中,AD∥BC,且AB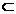 α,CD
α,CD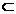 β,求证:AB,CD,l共点(相交于一点).
β,求证:AB,CD,l共点(相交于一点).
证明 ∵梯形ABCD中,AD∥BC,
∴AB,CD是梯形ABCD的两条腰.
∴ AB,CD必定相交于一点,
设AB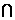 CD=M.
CD=M.
又∵AB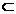 α,CD
α,CD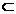 β,∴M∈α,且M∈β.∴M∈α
β,∴M∈α,且M∈β.∴M∈α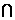 β.
β.
又∵α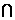 β=l,∴M∈l,
β=l,∴M∈l,
即AB,CD,l共点.
说明:证明多条直线共点时,一般要应用公理2,这与证明多点共线是一样的.
4.空间内五个点中的任意三点都不共线,由这五个点为顶点只构造出四个三棱锥,则这五个点最多可以确定 7个 个平面 .
3.对于空间三条直线,有下列四个条件:
①三条直线两两相交且不共点;②三条直线两两平行;
③三条直线共点;④有两条直线平行,第三条直线和这两条直线都相交.
其中,使三条直线共面的充分条件有 ( B )
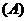 1个
1个 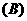 2个
2个
 3个
3个 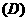 4个
4个
2.一个水平放置的平面图形的斜二测直观图是一个底角为 ,腰和上底边均为1的等腰梯形,则这个平面图形的面积是
( D )
,腰和上底边均为1的等腰梯形,则这个平面图形的面积是
( D )
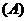
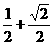
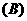
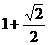

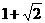
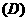
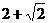
1. 、
、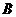 、
、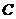 表示不同的点,
表示不同的点,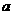 、
、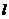 表示不同的直线,
表示不同的直线,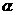 、
、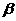 表示不同的平面,下列推理不正确的是
( C )
表示不同的平面,下列推理不正确的是
( C )
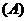
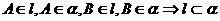
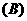
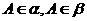 ,
,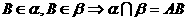 直线
直线

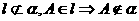
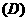
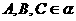 ,
,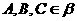 且
且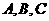 不共线
不共线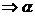 与
与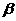 重合
重合
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.化简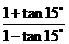 等于 (
等于 (  )
)
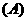
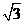
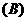


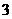
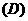
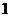
2.已知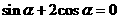 ,则
,则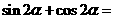
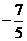 .
.
3.在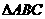 中,
中,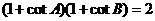 ,则
,则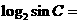
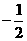 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com