
题目列表(包括答案和解析)
例1.已知双曲线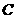 :
: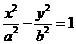
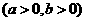 ,
,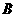 是右顶点,
是右顶点,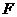 是右焦点,点
是右焦点,点 在
在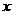 轴正半轴上,且满足
轴正半轴上,且满足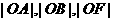 成等比数列,过点
成等比数列,过点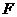 作双曲线在第一、三象限内的渐近线的垂线
作双曲线在第一、三象限内的渐近线的垂线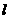 ,垂足为
,垂足为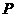 ,
,
(1)求证: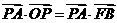 ;
;
(2)若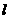 与双曲线
与双曲线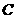 的左、右两支分别交于点
的左、右两支分别交于点 ,求双曲线
,求双曲线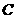 的离心率
的离心率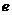 的取值范围.
的取值范围.
(1)证明:设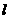 :
: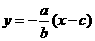 ,
,
由方程组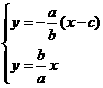 得
得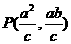 ,
,
∵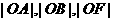 成等比数列,∴
成等比数列,∴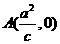 ,
,
∴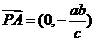 ,
,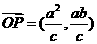 ,
,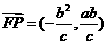 ,
,
∴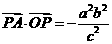 ,
,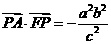 ,∴
,∴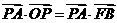 .
.
(2)设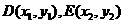 ,
,
由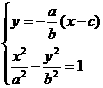 得
得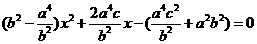 ,
,
∵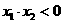 ,∴
,∴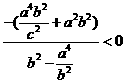 ,∴
,∴ ,即
,即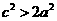 ,∴
,∴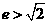 .
.
所以,离心率的取值范围为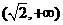 .
.
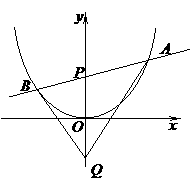
例2.如图,过抛物线 的对称轴上任一点
的对称轴上任一点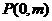
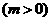 作直线与抛物线交于
作直线与抛物线交于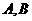 两点,点
两点,点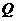 是点
是点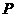 关于原点的对称点,
关于原点的对称点,
(1)设点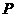 分有向线段
分有向线段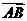 所成的比为
所成的比为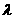 ,证明:
,证明: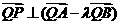 ;
;
(1)
设直线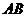 的方程是
的方程是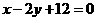 ,过
,过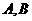 两点的圆
两点的圆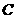 与抛物线在点
与抛物线在点 处有共同的切线,求圆
处有共同的切线,求圆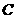 的方程.
的方程.
(2)
解:(1)设直线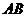 的方程为
的方程为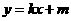 ,代入抛物线方程
,代入抛物线方程 得
得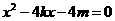
设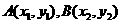 ,则
,则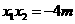 ,
,
∵点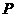 分有向线段
分有向线段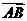 所成的比为
所成的比为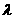 ,得
,得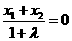 ,∴
,∴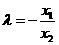 ,
,
又∵点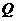 是点
是点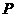 关于原点的对称点,∴
关于原点的对称点,∴ ,∴
,∴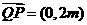 ,
,
∴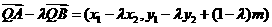
∴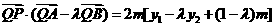
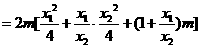
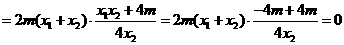
∴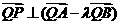 .
.
(2)由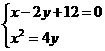 得点
得点 ,
,
由 得
得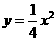 ,∴
,∴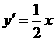 ,∴抛物线在点
,∴抛物线在点 处切线的斜率为
处切线的斜率为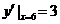 ,
,
设圆 的方程是
的方程是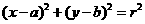 ,
,
则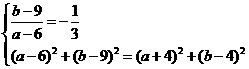 ,
,
解得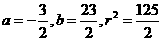 ,
,
∴圆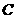 的方程是
的方程是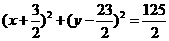 ,即
,即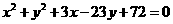 .
.
5.已知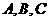 为抛物线
为抛物线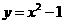 上三点,且
上三点,且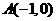 ,
,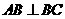 ,当
,当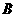 点在抛物线上移动时,点
点在抛物线上移动时,点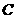 的横坐标的取值范围是
的横坐标的取值范围是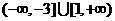 .
.
4.已知直线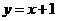 与椭圆
与椭圆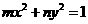
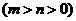 相交于
相交于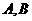 两点,若弦
两点,若弦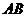 中点的横坐标为
中点的横坐标为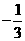 ,则双曲线
,则双曲线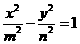 的两条渐近线夹角的正切值是
的两条渐近线夹角的正切值是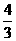 .
.
3.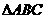 中,
中, 为动点,
为动点,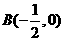 ,
,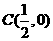 ,且满足
,且满足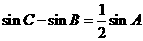 ,则动点
,则动点 的轨迹方程是(
的轨迹方程是(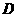 )
)
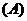
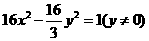
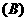
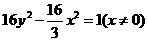

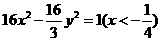
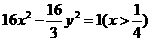
2.椭圆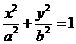
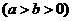 与
与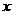 轴正半轴、
轴正半轴、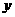 轴正半轴分别交于
轴正半轴分别交于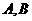 两点,在劣弧
两点,在劣弧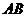 上取一点
上取一点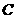 ,则四边形
,则四边形 的最大面积为(
的最大面积为(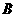 )
)
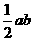
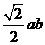


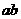
1.设抛物线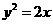 ,线段
,线段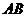 的两个端点在抛物线上,且
的两个端点在抛物线上,且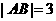 ,那么线段
,那么线段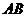 的中点
的中点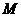 到
到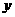 轴的最短距离是(
轴的最短距离是(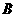 )
)
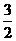
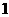

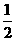
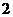
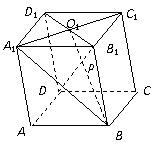
7.如图,在平行六面体ABCD-A1B1C1D1的中,A1C1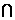 B1D1=O1,B1D
B1D1=O1,B1D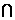 平面A1BC1=P.
平面A1BC1=P.
求证:P∈BO1.
证明 在平行六面体ABCD-A1B1C1D1中,
 ∵B1D
∵B1D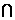 平面A1BC1=P,∴P∈平面A1BC1,P∈B1D.
平面A1BC1=P,∴P∈平面A1BC1,P∈B1D.
∵B1D 平面BB1D1D.∴P∈平面A1BC1,且P∈平面BB1D1D.
平面BB1D1D.∴P∈平面A1BC1,且P∈平面BB1D1D.
∴P∈平面A1BC1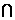 平面BB1D1D,
平面BB1D1D,
∵A1C1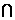 B1D1=O1,A1C1
B1D1=O1,A1C1 平面A1BC1,B1D1
平面A1BC1,B1D1 平面BB1D1D,
平面BB1D1D,
∴O1∈平面A1BC1,且O1∈平面BB1D1D.
又B∈平面A1BC1,且B∈平面BB1D1D,
∴平面A1BC1 平面BB1D1D=BO1.∴P∈BO1.
平面BB1D1D=BO1.∴P∈BO1.
说明一般地,要证明一个点在某条直线上,只要证明这个点在过这条直线的两个平面上.
|

|
版权所有:()
版权所有:()
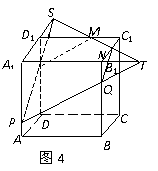
6.如图,P、Q、R分别是正方体ABCD-A1B1C1D1的棱AA1,BB1,DD1上的三点,试作出过P,Q,R三点的截面图.
作法 ⑴连接PQ,并延长之交A1B1的延长线于T;
⑵连接PR,并延长之交A1D1的延长线于S;
⑶连接ST交C1D1、B1C1分别于M,N,则线段MN
 为平面PQR与面A1B1C1D1的交线.
为平面PQR与面A1B1C1D1的交线.
⑷连接RM,QN,则线段RM,QN分别是平面PQR与面DCC1D1,面BCC1B1的交线.
得到的五边形PQNMR即为所求的截面图(如图4).
说明 求作二平面的交线问题,主要运用公理1.
解题关键是直接或间接找出二平面的两个确定的公共点.
有时同时还要运用公理2、3及公理的推论等知识.
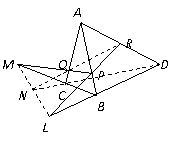
5.如图,P、Q、R分别是四面体ABCD的棱AB,AC,AD上的点,若直线PQ与直线BC的交点为M,直线RQ与直线DC的交点为N,直线PR与直线DB的交点为L,试证明M,N,L共线.
 证明:易证M,N,L∈平面PQR,且M,N,L∈平面BCD,
证明:易证M,N,L∈平面PQR,且M,N,L∈平面BCD,
所以M,N,L∈平面PQR 平面BCD,即M,N,L共线.
平面BCD,即M,N,L共线.
4. 四边形
四边形 中,
中,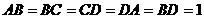 ,则成为空间四面体时,
,则成为空间四面体时, 的取值范围是
.
的取值范围是
.
答案: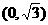 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com