
题目列表(包括答案和解析)
3.在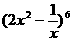 的展开式中常数项是
的展开式中常数项是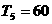 ;中间项是
;中间项是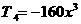 .
.
2.当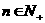 且
且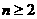 时,
时,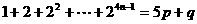 (其中
(其中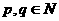 ,且
,且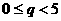 ),则
),则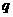 的值为
(
的值为
(  )
)
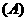 0
0
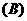 1
1
 2
2
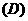 与
与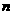 有关
有关
1.设二项式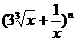 的展开式的各项系数的和为
的展开式的各项系数的和为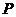 ,所有二项式系数的和为
,所有二项式系数的和为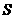 ,若
,若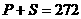 ,则
,则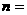 (
(  )
)
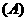 4
4
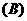 5
5
 6
6
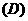 8
8
2.二项展开式的性质:
(1)在二项展开式中,与首末两端“等距离”的两项的二项式系数 .
(2)若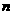 是偶数,则 的二项式系数最大;若
是偶数,则 的二项式系数最大;若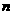 是奇数,则 的二项式系数最大.
是奇数,则 的二项式系数最大.
(3)所有二项式系数的和等于 .
(4)奇数项的二项式系数的和与偶数项的二项式系数的和 .
1.二项式定理: .
2.能利用二项展开式的通项公式求二项式的指数、求满足条件的项或系数.
1.掌握二项式定理和二项展开式的性质,并能用它们讨论整除、近似计算等相关问题.
9.已知(1+3x)n的展开式中,末三项的二项式系数的和等于 121,求展开式中系数最大的项.

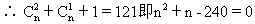
∴ n=15或 n=-16(舍)
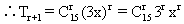
设第 r+1项与第 r项的系数分别为tr+1,tr
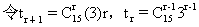
∴tr+1≥tr则可得3(15-r+1)>r解得r≤12
∴当r取小于12的自然数时,都有tr<tr+1当r=12时,tr+1=tr
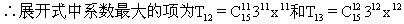
|

|
版权所有:()
版权所有:()
8.求证: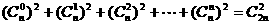
证明 由(1+x)n·(1+x)n=(1+x)2n,两边展开得:
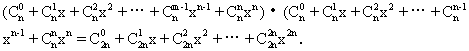
比较等式两边xn的系数,它们应当相等,所以有:

7.求满足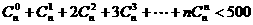 的最大整数
的最大整数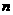 .
.

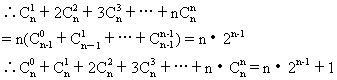
原不等式化为n·2n-1<499
∵27=128,∴n=8时,8·27=210=1024>500.
当n=7时,7·26=7×64=448<449.
故所求的最大整数为n=7.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com