
题目列表(包括答案和解析)
2.在棱长为 的正四面体
的正四面体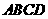 中,
中, 分别是
分别是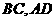 的中点,则
的中点,则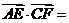 ( )
( )
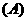
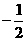
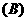
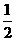

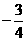
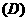

1.直线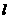 ,
, 和不同平面
和不同平面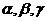 满足:
满足: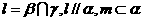 和
和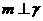 那么必有( )
那么必有( )
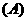
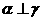 且
且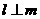
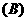
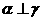 且
且

 且
且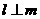
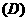
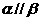 且
且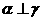
例1.已知斜三棱柱 中,
中,
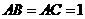 ,
,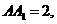 点
点 是
是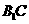 与
与 的交点,
的交点,
(1)基向量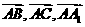 表示向量
表示向量 ;(2)求异面直线
;(2)求异面直线 与
与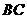 所成的角;
所成的角;
(3)判定平面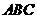 与平面
与平面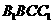
解:设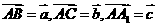
(1)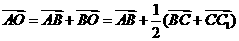
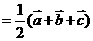
 (2)由题意,可求得
(2)由题意,可求得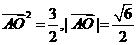 ,
,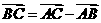 ,
,
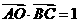 ,
,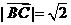 ,
,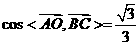 ,
,
∴异面直线 与
与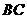 所成的角为
所成的角为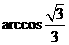
(3)取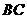 的中点
的中点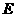 ,连结
,连结 ,则
,则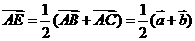
∵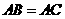 ,∴
,∴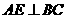 ,且
,且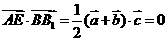 ,∴
,∴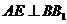
∴ ,
,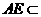 平面
平面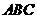 ,∴平面
,∴平面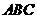 与平面
与平面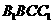
例2.如图在四棱锥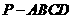 中,底面
中,底面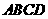 是
是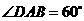 ,且边长为
,且边长为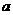 的菱形,侧面
的菱形,侧面 为正三角形,其所在平面垂直于底面
为正三角形,其所在平面垂直于底面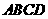 。
。
(1)若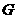 为
为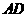 边的中点,求证:
边的中点,求证: 平面
平面 ;
;
(2)求二面角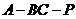 的大小;
的大小;
(3)若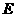 为
为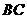 边的中点,能否在棱
边的中点,能否在棱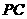 上找到一点
上找到一点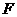 ,使平面
,使平面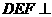 平面
平面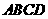 ,并证明你的结论。
,并证明你的结论。
(1)∵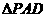 为正三角形,
为正三角形,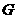 为
为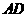 边的中点,∴
边的中点,∴ ,
,
 ∵平面
∵平面 垂直于底面
垂直于底面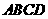 ,∴
,∴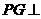 底面
底面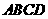 ,∴
,∴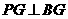
在菱形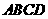 中,
中,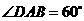 ,
, 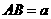
∴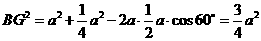 ,
,
∴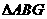 为直角三角形,
为直角三角形,
且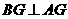 ,
,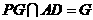 ,∴
,∴ 平面
平面
(2)由(1)知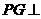 底面
底面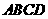 ,
,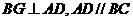 ,
,
∴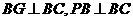 ,
,
∴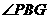 是二面角
是二面角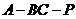 的平面角,
的平面角,
∵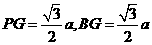 ,∴
,∴ ,∴
,∴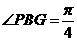
(3)∵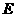 为
为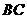 边的中点,∴
边的中点,∴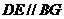 ,∴
,∴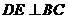 ,取
,取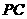 的中点
的中点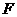 ,连结
,连结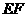 ,
,
则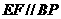 ,∵
,∵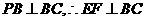 ,∴
,∴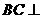 平面
平面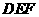 ,∴平面
,∴平面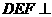 平面
平面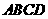 ,∴
,∴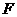 点存在,且为
点存在,且为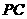 的中点。
的中点。
例3.如图,在直四棱柱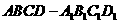 中,底面是边长为
中,底面是边长为 的菱形,侧棱长为
的菱形,侧棱长为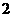
(1)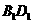 与
与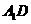 能否垂直?请证明你的判断;(2)当
能否垂直?请证明你的判断;(2)当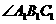 在
在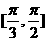 上变化时,求异面直线
上变化时,求异面直线 与
与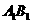 所成角的取值范围。
所成角的取值范围。
解:∵菱形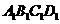 中,
中,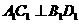 于
于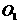 ,设
,设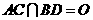 ,分别以
,分别以 所在直线为
所在直线为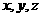 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设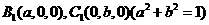 ,则
,则
 (1)∵
(1)∵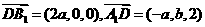 ,
,
∴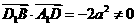
∴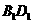 与
与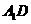 不能垂直。
不能垂直。
(2)∵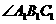
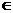
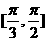 ,∴
,∴ ,
,
∵ ∴
∴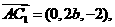
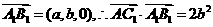 ,
,
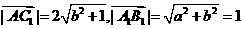 ,
,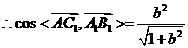
∵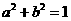 ,∴设
,∴设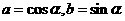 ,又
,又 ,
,
∴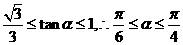
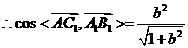
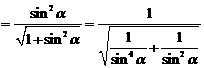
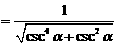
∵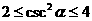 ,∴
,∴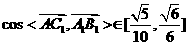
∴直线 与
与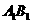 所成角的取值范围是
所成角的取值范围是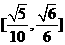 。
。
4.直角三角形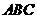 的斜边
的斜边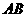 在平面
在平面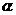 内,
内,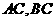 与平面
与平面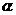 分别成
分别成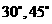 的角,若
的角,若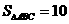 ,则
,则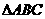 在平面
在平面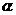 内的射影构成的三角形的面积为 5
内的射影构成的三角形的面积为 5
3.长方体的一个顶点上三条棱长分别为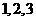 ,该长方体的顶点都在同一个球面上,则这个球的表面积为
,该长方体的顶点都在同一个球面上,则这个球的表面积为 
2.把正方形ABCD沿对角线AC折起,当A、B C、D四点为顶点的三棱锥体积最大时,直线BD与平面ABC所成的角的大小为( 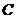 )
)
 90°
90°  60°
60°  45°
45° 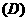 30°
30°
1.已知两条异面直线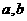 所成的角为
所成的角为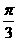 ,直线
,直线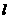 与
与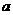 ,直线
,直线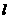 与
与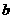 所成的角为
所成的角为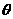 ,则
,则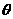 的范围是
(
的范围是
(  )
)
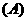
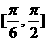
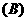
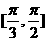

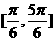
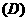
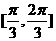
9.求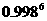 的近似值,使误差小于
的近似值,使误差小于 .
.
解:
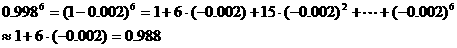
|

|
版权所有:()
版权所有:()
8.设 展开式中第2项的系数与第4项的系数的比为4:45,试求
展开式中第2项的系数与第4项的系数的比为4:45,试求 项的系数.
项的系数.
解:第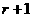 项
项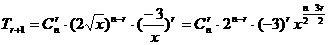 ,
,
∴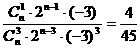 ,即
,即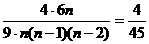 ,∴
,∴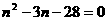 ,
,
∴ 或
或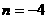 (舍负).
(舍负).
令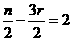 ,即
,即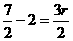 ,∴
,∴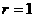 .
.
∴ 项的系数
项的系数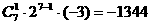 .
.
7.设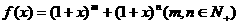 ,若展开式中关于
,若展开式中关于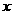 的一次项系数和为11,试问
的一次项系数和为11,试问 为何值时,含
为何值时,含 项的系数取得最小值.
项的系数取得最小值.
解:由题意知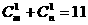 ,即
,即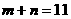 ,又展开式中含
,又展开式中含 项的系数
项的系数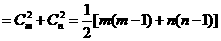
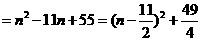 ,
,
∴当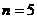 或
或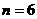 时,含
时,含 项的系数最小,最小值为
项的系数最小,最小值为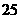 .
.
此时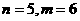 ;或
;或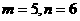 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com