
题目列表(包括答案和解析)
1.了解空间两条直线的位置关系.
7.点 是
是 所在平面外一点,
所在平面外一点, 分别是
分别是 、
、 、
、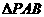 的重心,求证:(1)平面
的重心,求证:(1)平面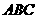
 平面
平面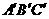 ;(2)求
;(2)求 .
.
证明:(1)如图,分别取 的中点
的中点 ,
,
连结 ,
,
∵ 分别是
分别是 、
、 、
、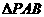 的重心,
的重心,
∴ 分别在
分别在 上,
上,
且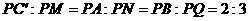 .
.
在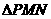 中,
中, ,故
,故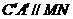 ,
,
又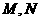 为
为 的边
的边 的中点,
的中点,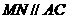 ,
,
∴ ,∴
,∴ 平面
平面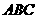 ,同理
,同理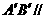 平面
平面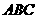
∴平面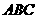
 平面
平面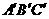 .
.
 (2)由(1)知
(2)由(1)知 ,
, ,
,
∴ .
.
|

|
版权所有:()
版权所有:()
6.若一直线与一个平面平行,则过平面内的一点且与这条直线平行的直线必在此平面内.
解:如图,设 ,
, ,
,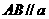 .由
.由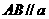 ,
,
∴它们确定一个平面 ,设
,设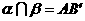 ,可证
,可证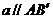 ,
,
 在平面
在平面 内,过点
内,过点 存在
存在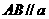 ,
,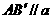 ,
,
∴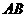 与
与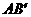 重合,即
重合,即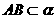 .
.
5.如图,A,B,C,D四点都在平面a,b外,它们在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,在b内的射影A2,B2,C2,D2在一条直线上,求证:ABCD是平行四边形.
证明:∵ A,B,C,D四点在b内的射影A2,B2,C2,D2在一条直线上,
∴A,B,C,D四点共面.
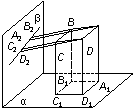 又A,B,C,D四点在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,
又A,B,C,D四点在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,
∴平面ABB1A1∥平面CDD1C1.
∴AB,CD是平面ABCD与平面ABB1A1,平面CDD1C1的交线.
∴AB∥CD.
同理AD∥BC.
∴四边形ABCD是平行四边形.
4.在长方体 中,经过其对角线
中,经过其对角线 的平面分别与棱
的平面分别与棱 、
、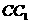 相交于
相交于 两点,则四边形
两点,则四边形 的形状为 .(平行四边形)
的形状为 .(平行四边形)
3.在正四棱柱 中,
中,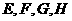 分别为棱
分别为棱 的中点,
的中点, 是
是 的中点,点
的中点,点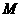 在四边形
在四边形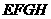 及其内部运动,则
及其内部运动,则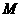 满足条件
满足条件
时,有 平面
平面 .(点
.(点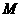 在线段
在线段 上)
上)
2. 是两个不重合平面,
是两个不重合平面, 是两条不重合直线,那么
是两条不重合直线,那么 的一个充分条件是( C )
的一个充分条件是( C )
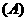
 ,
,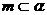 ,且
,且 ,
,

 ,
,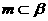 ,且
,且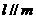

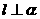 ,
, ,且
,且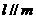
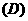
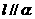 ,
, ,且
,且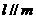
1.设线段 是夹在两平行平面
是夹在两平行平面 间的两异面线段,点
间的两异面线段,点 ,
, ,若
,若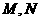 分别为
分别为 的中点,则有
(
的中点,则有
( 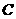 )
)
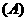
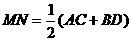



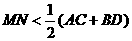
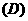
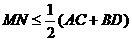
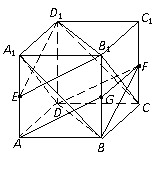
例1.正方体ABCD-A1B1C1D1中.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E、F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.
证明:(1)由B1B∥DD1,得四边形BB1D1D是平行四边形,
 ∴B1D1∥BD,
∴B1D1∥BD,
又BD Ë平面B1D1C,B1D1 平面B1D1C,
平面B1D1C,
∴BD∥平面B1D1C.
同理A1D∥平面B1D1C.
而A1D∩BD=D,
∴平面A1BD∥平面B1CD.
(2)由BD∥B1D1,得BD∥平面EB1D1.
取BB1中点G,∴AE∥B1G.
从而得B1E∥AG,同理GF∥AD.
∴AG∥DF.
∴B1E∥DF.
∴DF∥平面EB1D1.
∴平面EB1D1∥平面FBD.
说明 要证“面面平面”只要证“线面平面”,要证“线面平行”,只要证“线线平面”,故问题最终转化为证线与线的平行.
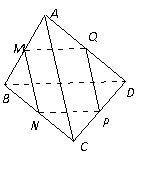
例2.如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
求证:(1)线段MP和NQ相交且互相平分;(2)AC∥平面MNP,BD∥平面MNP.
证明:(1) ∵M、N是AB、BC的中点,∴MN∥AC,MN= AC.
AC.
∵P、Q是CD、DA的中点,∴PQ∥CA,PQ= CA.
CA.
∴MN∥QP,MN=QP,MNPQ是平行四边形.
∴□MNPQ的对角线MP、NQ相交且互相平分.
(2)由(1),AC∥MN.记平面MNP(即平面MNPQ)为α.显然ACËα.
 否则,若ACÌα,
否则,若ACÌα,
由A∈α,M∈α,得B∈α;
由A∈α,Q∈α,得D∈α,则A、B、C、D∈α,
与已知四边形ABCD是空间四边形矛盾.
又∵MNÌα,∴AC∥α,
又AC Ëα,∴AC∥α,即AC∥平面MNP.
同理可证BD∥平面MNP.
小结:
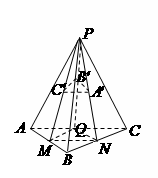
例3.已知正四棱锥 的底面边长为
的底面边长为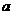 ,侧棱长为
,侧棱长为 ,点
,点 分别在
分别在 和
和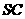 上,并且
上,并且 ,
, 平面
平面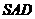 ,求线段
,求线段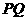 的长.
的长.
解:延长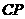 交
交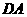 延长线于点
延长线于点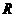 ,连
,连 ,可证得
,可证得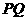 ∥
∥ ,由
,由 与
与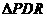 相似及已知求得
相似及已知求得 。在等腰
。在等腰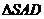 中,求出
中,求出 ,又在
,又在 中,由余弦定理求得
中,由余弦定理求得 。
。
∵ ,∴
,∴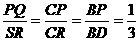 ,∴
,∴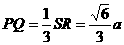 .
.
4.空间四边形 的两条对角线
的两条对角线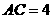 ,
,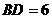 ,则平行于两对角线的截面四边形的周长的取值范围是
.答案:(8,12)
,则平行于两对角线的截面四边形的周长的取值范围是
.答案:(8,12)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com