
题目列表(包括答案和解析)
练习:(1)若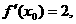 则
则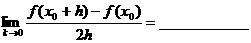
(2)若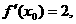 则
则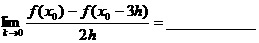
(3)若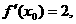 则
则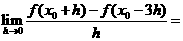 _______________
_______________
2.求下列函数的导数(1)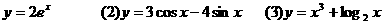
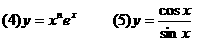
6.求单调区间的方法:
5. 函数单调性与导数:设函数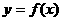 在区间(a,b)内有导数,如果____,则
在区间(a,b)内有导数,如果____,则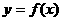 是这个区间内_____;如果在这个区间内___,则
是这个区间内_____;如果在这个区间内___,则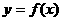 是这个区间内_____.
是这个区间内_____.
4.导数的运算法则: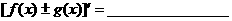


3.初等函数的导数公式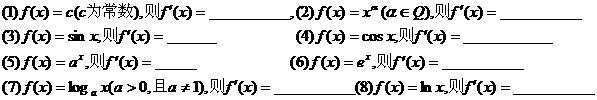
2.导数
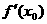 的几何意义:_________________________________________
的几何意义:_________________________________________
1.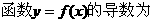
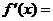
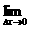 __________________
__________________
7.平行六面体ABCD-A1B1C1D1中,求证:CD1所在的直线与BC1所在的直线是异面直线.
 证明:假设CD1所在的直线与BC1所在的直线不是异面直线.
证明:假设CD1所在的直线与BC1所在的直线不是异面直线.
设直线CD1与BC1共面α.
∵C,D1∈CD1,B,C1∈BC1,∴C,D1,B,C1∈α.
∵CC1∥BB1,∴CC1,BB1确定平面BB1C1C,
∴C,B,C1∈平面BB1C1C.
∵不共线的三点C,B,C1只有一个平面,
∴平面α与平面BB1C1C重合.
∴D1∈平面BB1C1C,矛盾.
因此,假设错误,即CD1所在的直线与BC1所在的直线是异面直线.
|

|
版权所有:()
版权所有:()
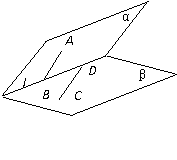
6.如图,已知平面α、β交于直线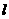 ,AB、CD分别在平面α,β内,且与
,AB、CD分别在平面α,β内,且与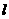 分别交于B,D两点.若∠ABD=∠CDB,试问AB,CD能否平行?并说明理由.
分别交于B,D两点.若∠ABD=∠CDB,试问AB,CD能否平行?并说明理由.
证明:直线AB,CD不能平行.否则,若AB∥CD,则AB∥CD共面,记这个平面为γ.
 ∴
AB,CD
∴
AB,CD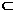 γ.
γ.
∴ AB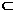 α,D∈γ.
α,D∈γ.
由题知,AB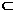 α,D∈α,且DÏAB,
α,D∈α,且DÏAB,
根据过一条直线及这条直线外一点,有且仅有一个平面,α与γ重合.
同理,β与γ重合.
∴ α与β重合,这与题设矛盾.
∴ AB,CD不能平行.
5.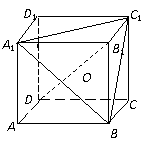 如图,在正方体ABCD-A1B1C1D1的中,求证:B1D被平面A1BC1分成1∶2的两段.
如图,在正方体ABCD-A1B1C1D1的中,求证:B1D被平面A1BC1分成1∶2的两段.
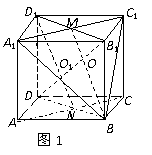
证明:如图1,在正方体ABCD-A1B1C1D1中,
连结B1D1,A1C1,BD,AC.
设B1D1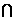 A1C1=M,BD
A1C1=M,BD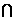 AC=N.
AC=N.
∴ M,N分别是B1D1,AC的中点.
连结BM,D1N.
∵ BB1∥DD1,且BB1=DD1,
∴ 四边形BDD1B1是平行四边形.
在平面BDD1B1中,设B1D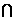 BM=O,B1D
BM=O,B1D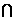 D1N=O1,
D1N=O1,
 在平行四边形BDD1B1中,
在平行四边形BDD1B1中,
∵ D1M∥NB,且D1M=NB,
∴ 四边形BND1M是平行四边形.
∴ BM∥ND1,即 OM∥O1D1,
∴ O是BO1的中点,即 O1O=OB1.
同理,OO1=O1D.
∴ O1O=OB1=O1D.
综上,OB1∶OD1=1∶2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com