
题目列表(包括答案和解析)
4、复数1+i+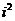 +…+
+…+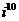 等于
[ ]
等于
[ ]
A.i
B. i C.2i D.
i C.2i D. 2i
2i
3、已知对于x的方程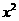 +(1
+(1 2i)x+3m
2i)x+3m i=0有实根,则实数m满足[ ]
i=0有实根,则实数m满足[ ]
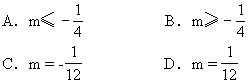
2、下列命题中,假命题是 [ ]
A.两个复数不可以比较大小B.两个实数可以比较大小
C.两个虚数不可以比较大小D.一虚数和一实数不可以比较大小
1、下列说法正确的是 [ ]
A.0i是纯虚数B.原点是复平面内直角坐标系的实轴与虚轴的公共点
C.实数的共轭复数一定是实数,虚数的共轭复数一定是虚数D.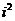 是虚数
是虚数
(四)巩固练习:
设复数z=3cosθ+2isinθ,求函数y=θ-argz(0<θ<)的最大值以及对应角θ的值.
[分析]先将问题实数化,将y表示成θ的目标函数,后利用代数法(函数的单调性、基本不等式等)以及数形结合法进行求解.
解法一、由0<θ<,得tanθ>0,从而0<argz<.
由z=3cosθ+2isinθ,得 tan(argz)==tanθ>0.
于是 tany=tan(θ-argz)===≤=.
当且仅当,即tanθ=时,取“=”.
又因为正切函数在锐角的范围内为增函数,故当θ=arctan时,y取最大值为arctan.
解法二、因0<θ<,故cosθ>0,sinθ>0,0<argz<,且
cos(argz)=,sin(argz)=.
显然y∈(-,),且siny为增函数.
siny=sin(θ-argz)=sinθcos(argz)-cosθsin(argz)=
==≤=.
当且仅当,即tanθ=,取“=”,此时ymax=arctan.
解法三、设Z1=2(cosθ+isinθ),Z2=cosθ,则Z=Z1+Z2,而Z1、Z2、Z的辐角主值分别为θ、0,argz.如图所示,必有y=∠ZOZ1,且0<y<.
在△ZOZ1中,由余弦定理得
 cosy==
cosy==
=+≥.
当且仅当4+5cos2θ=6,即cosθ=时,取“=”.
又因为余弦函数在0<θ<为减函数,故当θ=arccos时,ymax=arccos.
[说明]①解题关键点:将复数问题通过化归转化为实数问题,使问题能在我们非常熟悉的情景中求解.②解题规律:多角度思考,全方位探索,不仅使我们获得了许多优秀解法,而且还使我们对问题的本质认识更清楚,进而更有利于我们深化对复数概念的理解,灵活驾驭求解复数问题的能力.③解题易错点:因为解法的多样性,反三角函数表示角的不唯一性,因而最后的表述结果均不一样,不要认为是错误的.
(三)例题分析:
Ⅰ.2004年高考数学题选
1. (2004年四川卷理3)设复数ω=-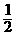 +
+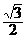 i,则1+ω=
i,则1+ω=
A.–ω B.ω2 C.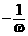 D.
D.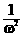
2.(2004重庆卷2))设复数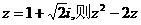 , 则
, 则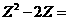 ( )
( )
A.–3 B.3 C.-3i D.3i
3. (2004高考数学试题广东B卷14)已知复数z与 (z +2)2-8i 均是纯虚数,则 z = .
Ⅱ.范例分析

①实数?②虚数?③纯虚数?
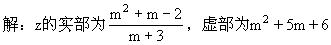
①复数z是实数的充要条件是:
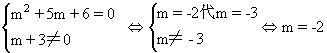
∴当m= 2时复数z为实数.
2时复数z为实数.
②复数z是虚数的充要条件:

∴当m≠ 3且m≠
3且m≠ 2时复数z为虚数
2时复数z为虚数
③复数z是纯虚数的充要条件是:
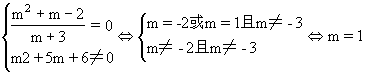
∴当m=1时复数z为纯虚数.
[说明]要注意复数z实部的定义域是m≠ 3,它是考虑复数z是实数,虚数纯虚数的必要条件.
3,它是考虑复数z是实数,虚数纯虚数的必要条件.
要特别注意复数z=a+bi(a,b∈R)为纯虚数的充要条件是a=0且b≠0.
 [ ]
[ ]
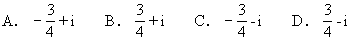

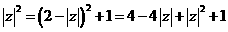 ,所以
,所以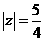 ,代入①得
,代入①得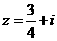 ,故选
,故选 .
.
解法3:选择支中的复数的模均为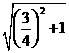 ,又
,又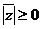 ,而方程右边为2+i,它的实部,虚部均为正数,因此复数z的实部,虚部也必须为正,故选择B.
,而方程右边为2+i,它的实部,虚部均为正数,因此复数z的实部,虚部也必须为正,故选择B.
[说明]解法1利用复数相等的条件;解法2利用复数模的性质;解法3考虑选择题的特点.
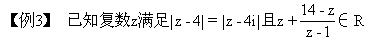
求:z
[分析]确定一个复数要且仅要两个实数a、b,而题目恰给了两个独立条件采用待定系数法可求出a、b确定z.
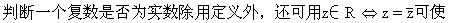
运算简化.
解:设z=x+yi(x,y∈R)
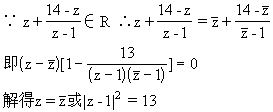
将z=x+yi代入|z 4|=|z
4|=|z 4i|可得x=y,∴z=x+xi
4i|可得x=y,∴z=x+xi

(2)当|z 1|
1|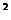 =13时,即有x
=13时,即有x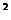
 x
x 6=0则有x=3或x=
6=0则有x=3或x= 2
2
综上所述故z=0或z=3+3i或z=-2 2i
2i
[说明]注意熟练地运用共轭复数的性质.其性质有:
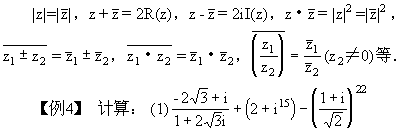
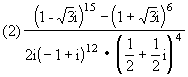
(3)1+2i+3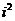 +…+1000
+…+1000
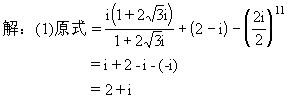
[说明]计算时要注意提取公因式,要注意利用i的幂的周期性,
要记住常用的数据: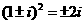 ,
,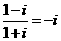 ,
,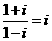 。
。
(2)原式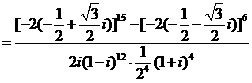
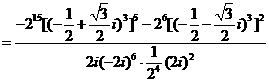
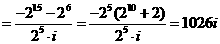

(3)解法1:原式=(1+2i 3
3 4i)+(5+6i
4i)+(5+6i 7
7 8i)+…+(997+998i
8i)+…+(997+998i 999
999 1000i)
1000i)
=250( 2
2 2i)=
2i)= 500
500 500i
500i
解法2:设S=1+2i+3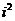 +…+1000
+…+1000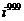 ,则iS=i+2
,则iS=i+2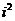 +3
+3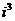 +…+999
+…+999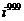 +1000
+1000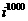 ,
,
∴(1 i)S=1+i+
i)S=1+i+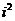 +…+
+…+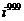
 1000
1000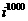
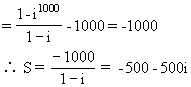
[说明]充分利用i的幂的周期性进行组合,注意利用等比数列求和的方法.
[例5](1)若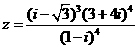 ,求:
,求: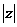
(2)已知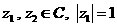 ,求
,求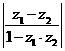 的值。
的值。
解:(1)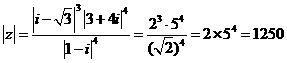


[例6]已知三边都不相等的三角形ABC的三内角A、B、C满足
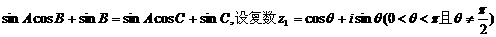 、
、
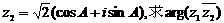 的值.
的值.
[解]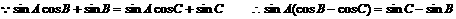
得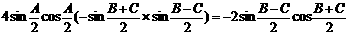 ……3分
……3分
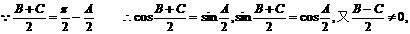
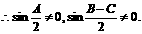 上式化简为
上式化简为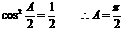 ……6分
……6分
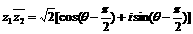 ……9分
……9分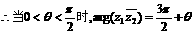
当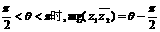 ……12分
……12分
[例7]设z1=1-cosθ+isinθ,z2=a2+ai(a∈R),若z1z2≠0,z1z2+=0,问在(0,2π)内是否存在θ使(z1-z2)2为实数?若存在,求出θ的值;若不存在,请说明理由.
[分析]这是一道探索性问题.可根据复数的概念与纯虚数的性质及复数为实数的充要条件,直接进行解答.
[解]假设满足条件的θ存在.
因z1z2≠0,z1z2+=0,故z1z2为纯虚数.
又z1z2=(1-cosθ+isinθ)(a2+ai)
=[a2(1-cosθ)-asinθ]+[a(1-cosθ)+a2sinθ]i,
于是,
由②知a≠0.
因θ∈(0,2π),故cosθ≠1.于是,由①得a=.
另一方面,因(z1-z2)2∈R,故z1-z2为实数或为纯虚数.又z1-z2=1-cosθ-a2+(sinθ-a)i,于是sinθ-a=0,或1-cosθ-a2=0.
若sinθ-a=0,则由方程组
得=sinθ,故cosθ=0,于是θ=或θ=.
若1-cosθ-a2=0,则由方程组
得()2=1-cosθ.
由于sin2θ=1-cos2θ=(1+cosθ)(1-cosθ),故1+cosθ=(1-cosθ)2.
解得cosθ=0,从而θ=或θ=.
综上所知,在(0,2π)内,存在θ=或θ=,使(z1-z2)2为实数.
[说明]①解题技巧:解题中充分使用了复数的性质:z≠0,z+=0Ûz∈{纯虚数}Û以及z2∈RÛz∈R或z∈{纯虚数}.(注:Re(z),Im(z)分别表示复数z的实部与虚部)
②解题规律:对于“是否型存在题型”,一般处理方法是首先假设结论成立,再进行正确的推理,若无矛盾,则结论成立;否则结论不成立.
[例8]设a为实数,在复数集C中解方程: z2+2|z|=a.
[分析]由于z2=a-2|z|为实数,故z为纯虚数或实数,因而需分情况进行讨论.
[解]设|z|=r.若a<0,则z2=a-2|z|<0,于是z为纯虚数,从而r2=2r–a.
解得 r=(r=<0,不合,舍去).故 z=±()i.
若a≥0,对r作如下讨论:
(1)若r≤a,则z2=a-2|z|≥0,于是z为实数.
解方程r2=a-2r,得r=(r=<0,不合,舍去).
故 z=±().
(2)若r>a,则z2=a-2|z|<0,于是z为纯虚数.
解方程r2=2r-a,得r=或r=(a≤1).
故 z=±()i(a≤1).
综上所述,原方程的解的情况如下:
当a<0时,解为:z=±()i;
当0≤a≤1时,解为:z=±(),z=±()i;
当a>1时,解为:z=±().
[说明]解题技巧:本题还可以令z=x+yi(x、y∈R)代入原方程后,由复数相等的条件将复数方程化归为关于x,y的实系数的二元方程组来求解.
[例9](2004年上海市普通高校春季高考数学试卷18)
已知实数 满足不等式
满足不等式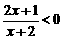 ,试判断方程
,试判断方程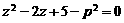 有无实根,并给出证明.
有无实根,并给出证明.
[解]由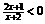 ,解得
,解得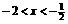 ,
,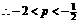 .方程
.方程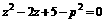 的判别式
的判别式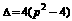 .
.
 ,
,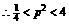 ,
, ,由此得方程
,由此得方程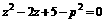 无实根.
无实根.
[例10]给定实数a,b,c.已知复数z1、z2、z3满足
求|az1+bz2+cz3|的值.
[分析]注意到条件(1),不难想到用复数的三角形式;注意到条件(2),可联想使用复数为实数的充要条件进行求解.
[解]解法一由=1,可设=cosθ+isinθ,=cosφ+isinφ,
则==cos(θ+φ)-isin(θ+φ).因=1,其虚部为0,
故0=sinθ+sinφ-sin(θ+φ)=2sincos-2sincos
=2sin(cos-cos)=4sinsinsin.
故θ=2kπ或φ=2kπ或θ+φ=2kπ,k∈Z.因而z1=z2或z2=z3或z3=z1.
若z1=z2,代入(2)得=±i,此时
|az1+bz2+cz3|=|z1|·|a+b±ci|=.
类似地,如果z2=z3,则|az1+bz2+cz3|=;
如果z3=z1,则|az1+bz2+cz3|=.
解法二由(2)知∈R,故 =, 即=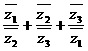 .
.
由(1)得=(k=1,2,3),代入上式,得=,
即z12z3+z22z1+z32z2=z22z3+z32z1+z12z2,分解因式,得(z1-z2)(z2-z3)(z3-z1)=0,
于是z1=z2或z2=z3或z3=z1.下同解法一.
[说明]①解题关键点是巧妙利用复数为实数的充要条件:z∈RÛz=,以及视,等为整体,从而简化了运算.
②解题易错点是拿到问题不加分析地就盲目动笔,而不注意充分观察题目的已知条件,结论特征等,从而使问题的求解或是变得异常的复杂,或干脆就无法解出最终的结果.
(二)知识点详析
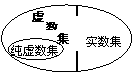
1.知识体系表解
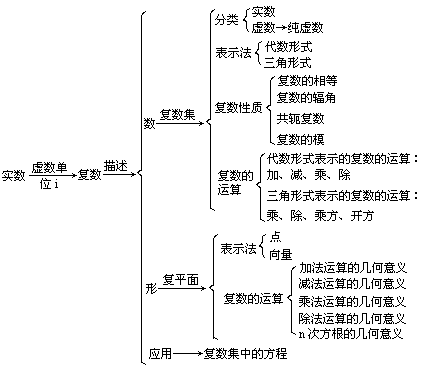
2.复数的有关概念和性质:
(1)i称为虚数单位,规定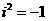 ,形如a+bi的数称为复数,其中a,b∈R.
,形如a+bi的数称为复数,其中a,b∈R.
(2)复数的分类(下面的a,b均为实数)

(3)复数的相等设复数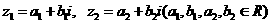 ,那么
,那么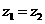 的充要条件是:
的充要条件是: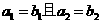 .
.
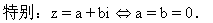
(4)复数的几何表示复数z=a+bi(a,b∈R)可用平面直角坐标系内点Z(a,b)来表示.这时称此平面为复平面,x轴称为实轴,y轴除去原点称为虚轴.这样,全体复数集C与复平面上全体点集是一一对应的.



复数z=a+bi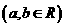 .在复平面内还可以用以原点O为起点,以点Z(a,b)
.在复平面内还可以用以原点O为起点,以点Z(a,b)
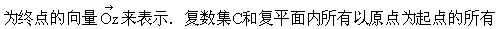
向量所成的集合也是一一对应的(例外的是复数0对应点O,看成零向量).
(7)复数与实数不同处
①任意两个实数可以比较大小,而任意两个复数中至少有一个不是实数时就不能比较大小.
②实数对于四则运算是通行无阻的,但不是任何实数都可以开偶次方.而复数对四则运算和开方均通行无阻.
3.有关计算:
⑴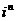
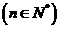 怎样计算?(先求n被4除所得的余数,
怎样计算?(先求n被4除所得的余数,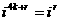
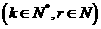 )
)
⑵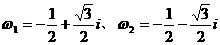 是1的两个虚立方根,并且:
是1的两个虚立方根,并且:
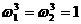
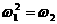
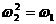
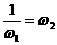
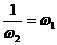

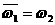
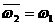
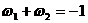
⑶
复数集内的三角形不等式是: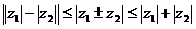 ,其中左边在复数z1、z2对应的向量共线且反向(同向)时取等号,右边在复数z1、z2对应的向量共线且同向(反向)时取等号。
,其中左边在复数z1、z2对应的向量共线且反向(同向)时取等号,右边在复数z1、z2对应的向量共线且同向(反向)时取等号。
⑷
棣莫佛定理是: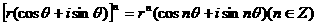
⑸
若非零复数 ,则z的n次方根有n个,即:
,则z的n次方根有n个,即:
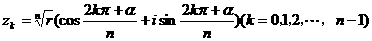
它们在复平面内对应的点在分布上有什么特殊关系?
都位于圆心在原点,半径为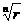 的圆上,并且把这个圆n等分。
的圆上,并且把这个圆n等分。
⑹
若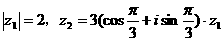 ,复数z1、z2对应的点分别是A、B,则△AOB(O为坐标原点)的面积是
,复数z1、z2对应的点分别是A、B,则△AOB(O为坐标原点)的面积是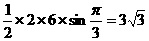 。
。
⑺
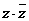 =
=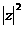 。
。
⑻ 复平面内复数z对应的点的几个基本轨迹:
①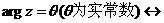 轨迹为一条射线。
轨迹为一条射线。
②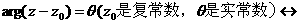 轨迹为一条射线。
轨迹为一条射线。
③ 轨迹是一个圆。
轨迹是一个圆。
④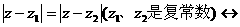 轨迹是一条直线。
轨迹是一条直线。
⑤ 轨迹有三种可能情形:a)当
轨迹有三种可能情形:a)当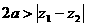 时,轨迹为椭圆;b)当
时,轨迹为椭圆;b)当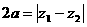 时,轨迹为一条线段;c)当
时,轨迹为一条线段;c)当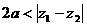 时,轨迹不存在。
时,轨迹不存在。
⑥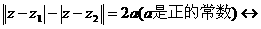 轨迹有三种可能情形:a)当
轨迹有三种可能情形:a)当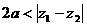 时,轨迹为双曲线;b)当
时,轨迹为双曲线;b)当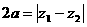 时,轨迹为两条射线;c)当
时,轨迹为两条射线;c)当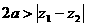 时,轨迹不存在。
时,轨迹不存在。
4.学习目标
(1)联系实数的性质与运算等内容,加强对复数概念的认识;
(2)理顺复数的三种表示形式及相互转换:z=r(cosθ+isinθ)Û(Z(a,b))Ûz=a+bi
(3)正确区分复数的有关概念;
(4)掌握复数几何意义,注意复数与三角、解几等内容的综合;
(5)正确掌握复数的运算:复数代数形式的加、减、乘、除;三角形式的乘、除、乘方、开方及几何意义;虚数单位i及1的立方虚根ω的性质;模及共轭复数的性质;
(6)掌握化归思想--将复数问题实数化(三角化、几何化);

 (7)掌握方程思想--利用复数及其相等的有关充要条件,建立相应的方程,转化复数问题。
(7)掌握方程思想--利用复数及其相等的有关充要条件,建立相应的方程,转化复数问题。
(一)主要知识:
1.数的概念的发展,复数的有关概念(实数、虚数、纯虚数、复数相等、共轭复数、模);
2.复数的代数表示与向量表示;
3.复数的加法与减法,复数的乘法与除法,复数的三角形式,复数三角形式的乘法与乘方,复数三角形式的除法与开方;
4.复数集中解实系数方程(包括一元二次方程、二项方程)。
复数在过去几年里是代数的重要内容之一,涉及的知识面广,对能力要求较高,是高考热点之一。但随着新教材对复数知识的淡化,高考试题比例下降,因此考生要把握好复习的尺度。
从近几年的高考试题上看:复数部分考查的重点是基础知识题型和运算能力题型。基础知识部分重点是复数的有关概念、复数的代数形式、三角形式、两复数相等的充要条件及其应用,复平面内复数的几何表示及复向量的运算。主要考点为复数的模与辐角主值,共轭复数的概念和应用。若只涉及到一、二个知识点的试题大都集中在选择题和填空题;若涉及几个知识点的试题,往往是中、高档题目,解答此类问题一般要抓住相应的概念进行正确的变换,对有些题目,往往用数形结合可获得简捷的解法。有关复数n次乘方、求辐角(主值)等问题,涉及到复数的三角形式,首先要将所给复数转化为三角形式后再进行变换。
复数的运算是高考中复数部分的热点问题。主要考查复数的代数和三角形式的运算,复数模及辐角主值的求解及复向量运算等问题。
基于上述情况,我们在学习“复数”一章内容时,要注意以下几点:
(1)复数的概念几乎都是解题的手段。因此在学习复数时要在深入理解、熟练掌握复数概念上下功夫。除去复数相等、模、辐角、共轭等外,还要注意一些重要而常不引起重视的概念。如:若有“3„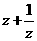 „4”。就是说
„4”。就是说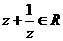 ,而且很快联系到
,而且很快联系到 或
或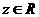 ,又∵
,又∵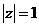 是不可能的,∴
是不可能的,∴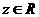 。
。
复数的三角形式和代数式,提供了将“复数问题实数化”的手段。
复数的几何意义也是解题的一个重要手段。
(2)对于涉及知识点多,与方程、三角、解析几何等知识综合运用的思想方法较多的题型,以及复数本身的综合题,一直成为学生的难点,应掌握规律及典型题型的技巧解法,并加以强化训练以突破此难点;
(3)重视以下知识盲点:
①不能正确理解复数的几何意义,常常搞错向量旋转的方向;
②忽视方程的虚根成对出现的条件是实系数;
③盲目地将实数范围内数与形的一些结论,不加怀疑地引用到复数范围中来;
④容易混淆复数的有关概念,如纯虚数与虚数的区别问题,实轴与虚轴的交集问题,复数辐角主值的范围问题等。
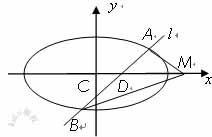
21、如图,斜率为k的直线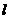 过椭圆
过椭圆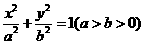 对称轴上的定点
对称轴上的定点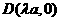 (
(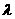 为非零常数,
为非零常数,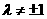 ),且
),且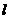 交椭圆于
交椭圆于 、
、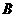 两点.
两点.
(1)当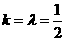 ,且线段
,且线段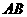 中点的横坐标等于
中点的横坐标等于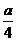 时,求椭圆的离心率;
时,求椭圆的离心率;
(2)试探究:在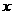 轴上是否存在定点
轴上是否存在定点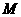 ,使
,使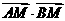 恒为定值?
恒为定值?
20、(如图,四棱锥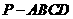 中,底面ABCD为矩形,
中,底面ABCD为矩形, 底面ABCD,AD=PD=1,AB=
底面ABCD,AD=PD=1,AB=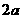 (
( ),E,F分别CD、PB的中点.
),E,F分别CD、PB的中点.
(1)求证:EF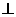 平面PAB;
平面PAB;
 (2)当
(2)当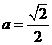 时,求AC与平面AEF所成角的正弦值.
时,求AC与平面AEF所成角的正弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com