
题目列表(包括答案和解析)
8.曲线y=x3+x-2 在点P0处的切线平行于直线y=4x-1,则点P0点的坐标是( B )
A.(0,1) B.(1,0) C.(-1,0) D.(1,4)
7.曲线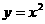 与曲线
与曲线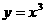 的公共切线的条数是
( B )
的公共切线的条数是
( B )
A.1条 B.2条 C.3条 D.0条
6.某物体的运动方程为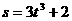 ,则该物体在
,则该物体在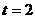 时的瞬时速率是( A )
时的瞬时速率是( A )
(A)36 (B)26 (C)14 (D)28
5.函数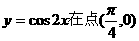 处的切线方程是 ( D )
处的切线方程是 ( D )
A.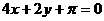 B.
B.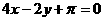
C.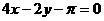 D.
D.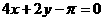
4.某质点的运动方程是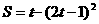 ,则在t=1s时的瞬时速度为( B )
,则在t=1s时的瞬时速度为( B )
A.-1 B.-3 C.7 D.13
3.设曲线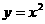 在点P处的切线斜率为3,则点P的坐标为 ( C )
在点P处的切线斜率为3,则点P的坐标为 ( C )
A.(3,9) B.(-3,9) C.(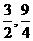 ) D.(
) D.(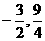 )
)
2.曲线y=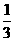 x3-x2+5,过其上横坐标为1的点作曲线的切线,则切线的倾斜角为 ( D )
x3-x2+5,过其上横坐标为1的点作曲线的切线,则切线的倾斜角为 ( D )
(A) 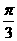 (B)
(B)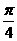 (C)
(C)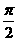 (D)
(D)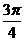
提示:y'=x2-2x. 当x=1时,y'=-1 选(D)
1.一质点在运动中经过的路程S和经历的时间t有关系S=5-3t2,则它在[1,+△t]内的平均速度为( C )
(A)3△t+6 (B)-3△t+6 (C)3△t-6 (D)-3△t-6
提示: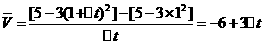 选(C)
选(C)
例1.求过抛物线y=ax2+bx+c(a≠0)上一点P(x0,y0)处的切线方程,并由此证实抛物线的光学性质。
分析:为求斜率,先求导函数:y'=2ax+b,故切线方程为y-y0=(2ax0+b)(x-x0)
即 y=(2ax0+b)x-ax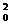 +c,亦即y=(2ax0+b)x-ax
+c,亦即y=(2ax0+b)x-ax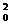 +c.
+c.
抛物线焦点:F(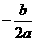 ,
,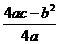 ),它关于切线的对称点之横坐标当x0,说明从焦点发出的光线射到(x0,y0)经抛物面反射后反射光线平行于对称轴,反之亦然。
),它关于切线的对称点之横坐标当x0,说明从焦点发出的光线射到(x0,y0)经抛物面反射后反射光线平行于对称轴,反之亦然。
要求过曲线上一点处的切线方程,一般先求出该点的导数值(斜率),再用点斜式写出后化简,同时我们还可以据此写出该点处的法线方程。
解:显然,y0=ax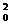 +bx0+c
+bx0+c
y'=2ax+b 故在P点处切线斜率为2ax0+b,
切线方程y-(ax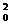 +bx0+c)=(2ax0+b)(x-x0),
+bx0+c)=(2ax0+b)(x-x0),
亦即y=(2ax0+b)x-ax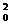 +c.
+c.
由于y=ax2+bx+c按向量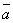 =
=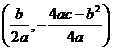 平移即得到y=ax2,只须证明过其上一点(x0,ax
平移即得到y=ax2,只须证明过其上一点(x0,ax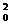 )的切线l :y=2ax0x-ax
)的切线l :y=2ax0x-ax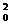 满足:焦点关于l的对称点为(m,n).
满足:焦点关于l的对称点为(m,n).
当x0≠0时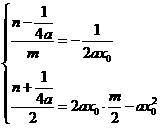 ,消去n. 知 m=x0.
,消去n. 知 m=x0.
当x0=0时,切线为y=0,F之对称点横坐标显然是0,
故从焦点发出的光线射到(x0,ax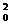 )后被抛物面反射后的方程为x=x0(与对称轴平行);反之,与对称轴平行的光线被抛物面反射后必聚汇于焦点.
)后被抛物面反射后的方程为x=x0(与对称轴平行);反之,与对称轴平行的光线被抛物面反射后必聚汇于焦点.
例2.求函数y=x4+x-2 图象上的点到直线y=x-4的距离的最小值及相应点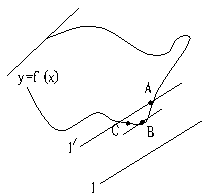 的坐标.
的坐标.
分析:首先由 得x4+2=0 知,两曲线无交点.
得x4+2=0 知,两曲线无交点.
y'=4x3+1,切线要与已知直线平行,须4x3+1=1,x=0.
故切点:(0 , -2)
一般地,当直线l与y=f(x)的图像无交点时,与l平行的切线与l间距离应为图像上点到l的 距离的最值,以最小值为例(如图)与l平行的 直线若与曲y=f(x)相交,(A为一交点),则l'与l间必存在y=f(x)上的点C,显然,C点到l的距离小于l与l'间的距离,亦即A到l的距离.
当然,我的也可用参数直接考虑:设(x0,x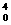 +x0-2)为y=f(x)图象上任意一点,它到l的距离
+x0-2)为y=f(x)图象上任意一点,它到l的距离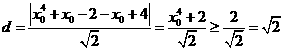 ,故距离最小距离为
,故距离最小距离为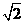
上述等号当且仅当x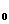 =0时取得,故相应点坐标为(0,
=0时取得,故相应点坐标为(0,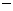 2)。
2)。
解:y'= 4x3+1,令4x3+1=1,x=0. 由此知过曲线上点(0,-2)的切线方程y=x+2 与已知直线平行,它到 已知直线距离最近,为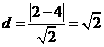 .
.
例3.已知一直线l经过原点且与曲线y=x3-3x2+2x相切,试求直线l的方程。
分析: 设切点为(x0,y0),则y0=x03-3x02+2x0,由于直线l经过原点,故等式的两边同除以x0即得切线的斜率,再根据导数的几何意义求出曲线在点x0处的切线斜率,便可建立关于x0的方程。在两边同除以x0时,要注意对x0是否为0进行讨论。
解:设直线l:y=kx 。 ∵y'=3x2-6x+2, ∴y'|x=0=2,又∵直线与曲线均过原点,于是直线y=kx与曲线y=x3-3x2+2相切于原点时,k=2。
若直线与曲线切于点(x0,y0) (x0≠0),则k=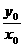 ,∵y0=x03-3x02+2x0,
,∵y0=x03-3x02+2x0,
∴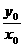 =x02-3x0+2,
=x02-3x0+2,
又∵k=y'|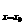 =3x02-6x0+2,
=3x02-6x0+2,
∴x02-3x0+2=3x02-6x0+2, ∴2x02-3x0=0,
∵x0≠0, ∴x0=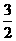 , ∴k=x02-3x0+2=-
, ∴k=x02-3x0+2=-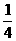 ,
,
故直线l的方程为y=2x或y=-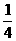 x。
x。
例4.已知曲线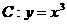 及其上一点
及其上一点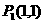 ,过
,过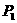 作C的切线
作C的切线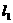 ,
,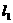 与C的另一公共点为
与C的另一公共点为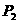 (不同于
(不同于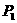 ),过
),过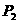 作C的切线
作C的切线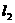 ,
,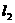 与C的另一公共点为
与C的另一公共点为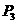 (不同于
(不同于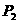 ),…,得到C的一列切线
),…,得到C的一列切线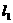 ,
,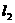 ,…,
,…,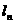 ,…,相应的切点分别为
,…,相应的切点分别为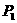 ,
,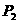 ,…,
,…, ,…。
,…。
(1)求 的坐标;
的坐标;
(2)设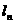 到
到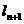 的角为
的角为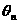 ,求
,求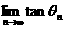 之值。
之值。
解:(1)设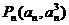 ,过
,过 作C的切线。
作C的切线。
C在 处的切线
处的切线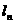 的方程为:
的方程为: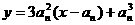 ,代入
,代入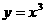 ,并整理得
,并整理得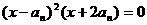 。
。
即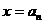 (舍去)或
(舍去)或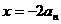 。
。
由题意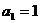 ,
,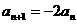 ,从而
,从而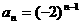 ,(n∈N*)
,(n∈N*)
即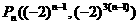 ;
;
(2)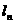 的斜率
的斜率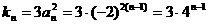 。
。
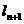 的斜率
的斜率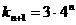 。
。
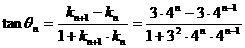 。
。
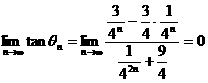
例5.在直线轨迹上运行的一列火车,从刹车到停车这段时间内,测得刹车后t秒内列车前进的距离s=27t-0.45t2(单位是米),这列火车在刹车后几秒钟才停车?刹车后又运行了多少米?
解:当火车运行速度为0时,火车停车。
v=s'=(27t-0.45t2)'=27-0.9t,
令27=0.9t=0,得t=30(秒),
则s=27×30-0.45×302=405(米),
故这列火车在刹车后30秒钟才停车,刹车后又运行了405米。
例6.求曲线y=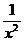 在横坐标为x0的点处的切线方程,并求此曲线的切线被两坐标轴所截线段的最短长度。
在横坐标为x0的点处的切线方程,并求此曲线的切线被两坐标轴所截线段的最短长度。
分析:先根据导数的几何意义求出曲线在点x0处的切线方程,从而求出切线被两坐标轴所截线段,再用基本不等式求其最小值。
解:由导数的定义可得y /=-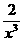 ,则过(
,则过(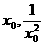 )点的切线方程为
)点的切线方程为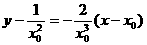 ,由此得切线在x轴与y轴上的交点分别为A(
,由此得切线在x轴与y轴上的交点分别为A(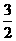 x0,0),B(0,
x0,0),B(0,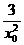 )。
)。
则|AB|2=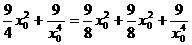 ≥
≥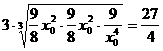 ,
,
∴|AB|≥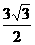 ,当且仅当
,当且仅当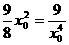 ,即x0=±
,即x0=± 时,等号成立。故最短长度为
时,等号成立。故最短长度为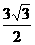 。
。
 例7.如图,已知圆心为O,半径为1的圆与直线l相切于点A,一动点P自切点A沿直线l向右移动时,取弧AC的长为
例7.如图,已知圆心为O,半径为1的圆与直线l相切于点A,一动点P自切点A沿直线l向右移动时,取弧AC的长为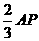 ,
,
直线PC与直线AO交于点M。又知当AP=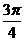 时,点P的速度
时,点P的速度
为v,求这时点M的速度。(1984年·全国高考附加题)
 分析: 设AP的长为x,AM的长为y,用x表示y,并用复合函数求导法则对时间t进行求导。
分析: 设AP的长为x,AM的长为y,用x表示y,并用复合函数求导法则对时间t进行求导。
解:如图,作CD⊥AM,并设AP=x,AM=y,∠COA=θ,
由题意弧AC的长为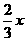 ,半径OC=1,可知θ=
,半径OC=1,可知θ=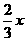 ,考虑θ∈(0,π)。
,考虑θ∈(0,π)。
∵△APM∽△DCM,∴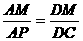 。
。
∵DM=y- (1-cos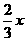 ),DC=sin
),DC=sin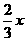 ,∴
,∴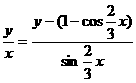
∴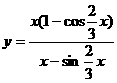 。
。
上式两边对时间t进行求导,则
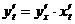 。
。
∴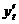 =
=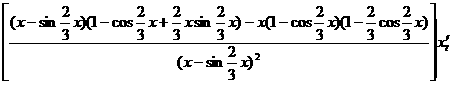
当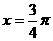 时,
时,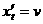 ,代入上式得点M的速度
,代入上式得点M的速度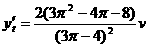 。
。
例8.已知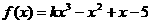 在R上单调递增,记
在R上单调递增,记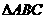 的三内角
的三内角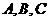 的对应边分别为
的对应边分别为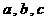 ,若
,若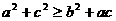 时,不等式
时,不等式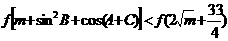 恒成立.
恒成立.
(Ⅰ)求实数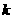 的取值范围;
的取值范围;
(Ⅱ)求角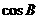 的取值范围;
的取值范围;
(Ⅲ)求实数 的取值范围.
的取值范围.
解:(1)由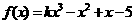 知
知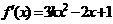 ,
,
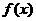 在R上单调递增,
在R上单调递增,

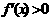 恒成立,
恒成立,
 且
且 ,即
,即 且
且 ,
,
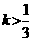 ,
,
当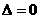 ,即
,即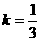 时,
时,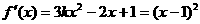 ,
,

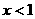 时
时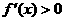 ,
,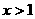 时,
时,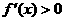 ,即当
,即当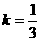 时,能使
时,能使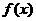 在R上单调递增,
在R上单调递增,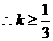 .
.
(2)
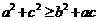 ,由余弦定理:
,由余弦定理: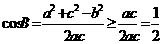 ,
,
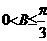 ,
,
(3)
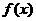 在R上单调递增,且
在R上单调递增,且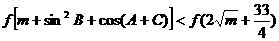 ,
,
所以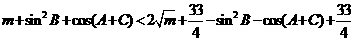
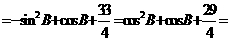
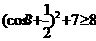 ,
,
故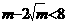 ,即
,即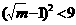 ,
,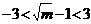 ,即
,即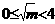 ,即
,即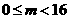 .
.
例9.已知函数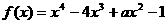 在区间
在区间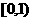 单调递增,在区间
单调递增,在区间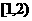 单调递减.
单调递减.
(Ⅰ)求a的值;
(Ⅱ)若点A(x0,f(x0))在函数f(x)的图象上,求证点A关于直线x=1的对称点B也在函数f(x)的图象上;
(Ⅲ)是否存在实数b,使得函数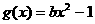 的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的值;若不存在,试说明理由.
的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的值;若不存在,试说明理由.
解:(Ⅰ)由函数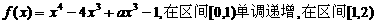 单调递减,
单调递减,
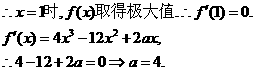
(Ⅱ)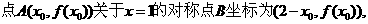

(Ⅲ)函数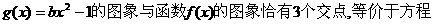

物体在时刻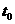 时的瞬时速度
时的瞬时速度 就是物体运动规律
就是物体运动规律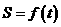 在
在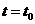 时的导数
时的导数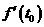 ,即有
,即有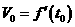 。
。
利用导数的这个物理意义,可以帮助我们获得按规律运动的物体的瞬时速度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com