
题目列表(包括答案和解析)
16.路灯距地面8m,一身高1.6m的人沿穿过灯下的直路以84m/min的速度行走,则人影长度变化速率是多少?(要求以m/s为单位)
解: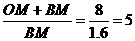 .
.
 ∴OM= 4BM
∴OM= 4BM
同理ON=4CN
两式相减,知,影长变化BM-CN=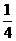 (OM-ON)
(OM-ON)
=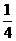 MN=
MN=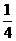 ·△t·84m/min
·△t·84m/min
∴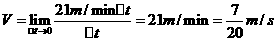 .
.
15.由y=0,x=8,y=x2围成的曲边三角形,在曲线弧OB上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围成的三角形PQA面积最大。
答案:(16/3,256/3)
14.求过点P(2,2)且与曲线y=x2相切的直线方程.
解:y'=2x,过其上一点(x0,x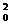 )的切线方程为
)的切线方程为
y-x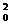 =2x0(x-x0),过P(2,2),故2-x
=2x0(x-x0),过P(2,2),故2-x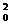 =2x0(2-x0)
=2x0(2-x0)
x0=2±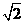 . 故切线方程为y=(4±
. 故切线方程为y=(4±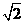 )x-(6±
)x-(6±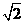 ).
).
13.求曲线y = sinx在点x=π处的切线方程。
提示:根据导数的几何意义求出曲线y = sinx在点x=π处的切线斜率。
解:∵y′=cosx,∴切线的斜率k= = -1,
= -1,
∴切线方程为 y- 0=- (x- π),即x+y-π=0。
12.曲线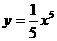 上一点M处的切线与直线
上一点M处的切线与直线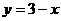 垂直,则切线的方程是_______________________
垂直,则切线的方程是_______________________ 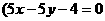 或
或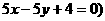
11.如果曲线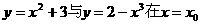 处的切线互相垂直,则x0的值为
. (
处的切线互相垂直,则x0的值为
. (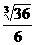 )
)
10.已知二函数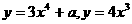 ,若它们的图象有公共点,且在公共点处的切线重合,则切斜线率为 ( C
)
,若它们的图象有公共点,且在公共点处的切线重合,则切斜线率为 ( C
)
A.0 B.12 C.0或12 D.4或1
9.已知函数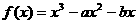 的图象与x轴切于点(1,0),则
的图象与x轴切于点(1,0),则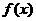 的极值为( A )
的极值为( A )
A.极大值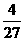 ,极小值0 B.极大值0,极小值
,极小值0 B.极大值0,极小值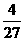
C.极小值-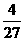 ,极大值0 D.极大值-
,极大值0 D.极大值-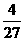 ,极小值0
,极小值0
8.函数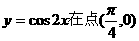 处的切线方程是 ( D )
处的切线方程是 ( D )
A.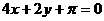 B.
B.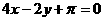
C.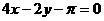 D.
D.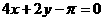
9.给出下列命题:
(1)若函数f(x)=|x|,则f’(0)=0;
(2)若函数f(x)=2x2+1,图象上P(1,3)及邻近上点Q(1+Δx,3+Δy),则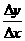 =4+2Δx
=4+2Δx
(3)加速度是动点位移函数S(t)对时间t的导数;
(4)y=2cosx+lgx,则y’=-2cosx·sinx+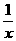 其中正确的命题有( B
)
其中正确的命题有( B
)
A. 0个 B.1个 C.2个 D.3个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com