
题目列表(包括答案和解析)
1.在下列结论中,正确的结论有 (  )
)
①单调增函数的导函数也是单调增函数; ②单调减函数的导函数也是单调减函数;
③单调函数的导函数也是单调函数; ④导函数是单调,则原函数也是单调的.
 0个
0个 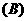 2个
2个  3个
3个 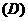 4个
4个
3.函数的最值:
①求函数 在区间
在区间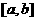 上的极值;②将极值与区间端点函数值
上的极值;②将极值与区间端点函数值 比较,其中最大的一个就是最大值,最小的一个就是最小值.
比较,其中最大的一个就是最大值,最小的一个就是最小值.
2.函数的极值:
(1)概念:函数 在点
在点 附近有定义,且若对
附近有定义,且若对 附近的所有点都有
附近的所有点都有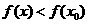 (或
(或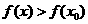 ),则称
),则称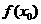 为函数的一个极大(小)值,称
为函数的一个极大(小)值,称 为极大(小)值点.
为极大(小)值点.
(2)求函数极值的一般步骤:
①求导数 ;②求方程
;②求方程 的根;③检验
的根;③检验 在方程
在方程 的根的左右的符号,如果是左正右负(左负右正),则
的根的左右的符号,如果是左正右负(左负右正),则 在这个根处取得极大(小)值.
在这个根处取得极大(小)值.
1.函数的单调性:
设函数在某区间内可导,则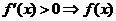 在该区间上单调递增;
在该区间上单调递增;
 在该区间上单调递减.
在该区间上单调递减.
反之,若 在某区间上单调递增,则在该区间上有
在某区间上单调递增,则在该区间上有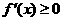 恒成立(但不恒等于0);
恒成立(但不恒等于0);
若 在某区间上单调递减,则在该区间上有
在某区间上单调递减,则在该区间上有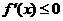 恒成立(但不恒等于0).
恒成立(但不恒等于0).
2.了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号),会求一些实际问题的最大值和最小值.
1.了解可导函数的单调性与其导数的关系;
20.曲线:y=ax3+bx2+cx+d在(0,1)点处的切线为l1:y=x+1,在(3,4)点处的切线为l2:y=-2x+10,求曲线C的方程。
分析:已知两点均在曲线C上,y'=3ax2+2bx+c 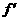 (0)=c,
(0)=c, 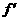 (3)=27a+6b+c
(3)=27a+6b+c
l1:y=cx+1 l2:y=(27a+6b+c)(x-3)+4
与已知比较,分别求出d=1,c=1,a=- ,b=1.
,b=1.
答案:C:y=- x3+x2+x+1.
x3+x2+x+1.
说明:求曲线过一点处的切线,先求斜率--即导函数在x0处的值,再用点斜式写出化简.
|

|
版权所有:()
版权所有:()
19.曲线y=x(x+1)(2-x)上有一点P,它的坐标均为整数,且过P点的切线斜率为正数,求此点坐标及相应的切线方程.
解:y=-x3+x2+2x y'=-3x2+2x+2
令y'>0 知x∈(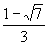 ,
,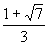 )
)
又x∈z ∴x=0或1 ∴P点坐标为(0,0)或(1,2).
切线斜率k=2或1,
切线方程为y=2x或y=x+1.
18.设曲线S:y=x3-6x2-x+6,S在哪一点处的切线斜率最小?设此点为P(x0,y0)求证:曲线S关于P点中心对称.
解:y'=3x2-12x-1当x=2时有最小值.故P:(2, -12).
S在(2,-12)处的切线斜率最小,为-13.
又y=(x-2+2)3-6(x-2+2)2-(x-2+2)+6
=(x-2)3-13(x-2) -12
故曲线C的图象按向量 =(-2,+12)平移后方程为y'=x
=(-2,+12)平移后方程为y'=x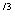 -13x'为奇数,关于原点对称,
-13x'为奇数,关于原点对称,
故P(2,-12)为曲线S的对称中心.
17.已知直线y=3x+1是曲线y=x3-2x+a的一条切线,求a的值.
解:y'=3x2-2. 令3x2-2=3,
x=± .代入切线方程知y0=1±
.代入切线方程知y0=1± ,
,
∴a=y0+2x0-x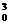 =
= .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com