
题目列表(包括答案和解析)
3.函数的运算法则成立的前提条件是函数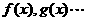 的极限存在,在进行极限运算时,要特别注意这一点.
的极限存在,在进行极限运算时,要特别注意这一点.
2.有限个函数的和(或积)的极限等于这些函数的和(或积);
 如果
如果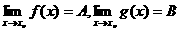 ,那么
,那么
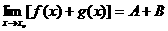
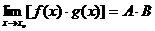
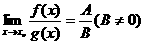
也就是说,如果两个函数都有极限,那么这两个函数的和、差、积、商组成的函数极限,分别等于这两个函数的极限的和、差、积、商(作为除数的函数的极限不能为0).
说明:当C是常数,n是正整数时,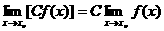
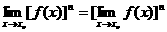
这些法则对于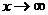 的情况仍然适用.
的情况仍然适用.
三 典例剖析
例1.求下列函数在X=0处的极限
(1)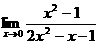 (2)
(2)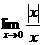 (3)
(3)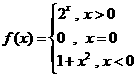
例2 求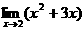
例3 求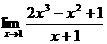
例4 求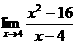
分析:当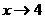 时,分母的极限是0,不能直接运用上面的极限运用法则.注意函数
时,分母的极限是0,不能直接运用上面的极限运用法则.注意函数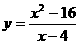 在定义域
在定义域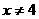 内,可以将分子、分母约去公因式
内,可以将分子、分母约去公因式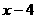 后变成
后变成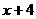 ,由此即可求出函数的极限.
,由此即可求出函数的极限.
例5 求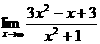
分析:当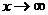 时,分子、分母都没有极限,不能直接运用上面的商的极限运算法则.如果分子、分母都除以
时,分子、分母都没有极限,不能直接运用上面的商的极限运算法则.如果分子、分母都除以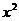 ,所得到的分子、分母都有极限,就可以用商的极限运用法则计算。
,所得到的分子、分母都有极限,就可以用商的极限运用法则计算。
总结: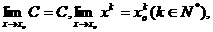
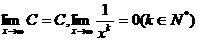
例6 求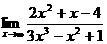
分析:同例5一样,不能直接用法则求极限. 如果分子、分母都除以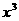 ,就可以运用法则计算了。
,就可以运用法则计算了。
四 课堂练习(利用函数的极限法则求下列函数极限)
(1)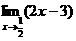 ;
(2)
;
(2)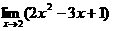
(3)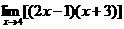 ; (4)
; (4)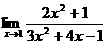
(5)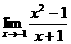 (6)
(6)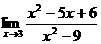
(7) (8)
(8)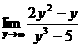
五 小结
1.函数极限存在的条件;如何求函数的极限。
特别地,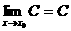 ;
;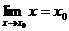
8.(2003年普通高等学校招生全国统一考试(上海理17))
已知复数z1=cosθ-i,z2=sinθ+i,求|z1·z2|的最大值和最小值.
7.设z1,z2是两个虚数,且z1+z2=-3,|z1|+|z2|=4.若θ1=argz1,θ2=argz2,求cos(θ1-θ2)的最大值.
6、若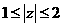 ,求
,求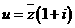 所对应的点A的集合表示的图形,并求其面积.
所对应的点A的集合表示的图形,并求其面积.
5、设A,B,C三点对应的复数分别为z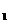 ,z
,z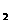 ,z
,z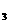 满足
满足

(1)证明:△ABC是内接于单位圆的正三角形;
(2)求S△ABC;
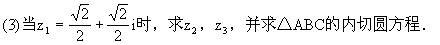
4、已知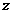 是虚数,
是虚数, 是实数。
是实数。
(1)求z对应复平面内动点A的轨迹;
(2)设u=3iz+1,求u对应复平面内动点B的轨迹;
(3)设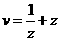 ,求
,求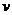 对应复平面内动点C的轨迹。
对应复平面内动点C的轨迹。
3、在复平面上绘出下列图形:
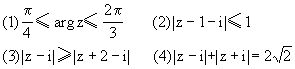
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com