
题目列表(包括答案和解析)
13.(上海20)(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分7分.
已知双曲线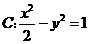 .
.
(1)求双曲线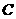 的渐近线方程;
的渐近线方程;
(2)已知点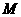 的坐标为
的坐标为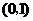 .设
.设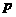 是双曲线
是双曲线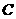 上的点,
上的点,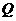 是点
是点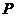 关于原点的对称点.
关于原点的对称点.
记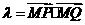 .求
.求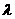 的取值范围;
的取值范围;
(3)已知点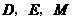 的坐标分别为
的坐标分别为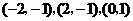 ,
,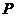 为双曲线
为双曲线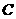 上在第一象限内的点.记
上在第一象限内的点.记 为经过原点与点
为经过原点与点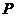 的直线,
的直线,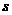 为
为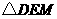 截直线
截直线 所得线段的长.试将
所得线段的长.试将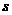 表示为直线
表示为直线 的斜率
的斜率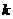 的函数.
的函数.
[解](1)所求渐近线方程为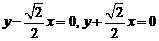 ……………...3分
……………...3分
(2)设P的坐标为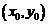 ,则Q的坐标为
,则Q的坐标为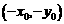 , …………….4分
, …………….4分
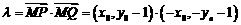
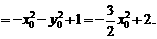 ……………7分
……………7分
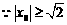
 的取值范围是
的取值范围是 ……………9分
……………9分
(3)若P为双曲线C上第一象限内的点,
则直线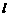 的斜率
的斜率 ……………11分
……………11分
由计算可得,当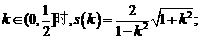
当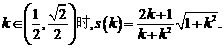 ……………15分
……………15分
∴ s表示为直线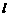 的斜率k的函数是
的斜率k的函数是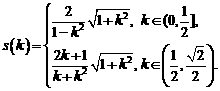 ….16分
….16分
8.(2008湖南19)(本小题满分13分)
已知椭圆的中心在原点,一个焦点是F(2,0),且两条准线间的距离为λ(λ>4).
(Ⅰ)求椭圆的方程; (Ⅱ)若存在过点A(1,0)的直线l,使点F关于直线l的对称点在椭圆上,求λ的取值范围.
解 (Ⅰ)设椭圆的方程为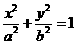 (a>b>0).
(a>b>0).
由条件知c=2,且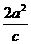 =λ,所以a2=λ,
=λ,所以a2=λ,
b2=a2-c2=λ-4.故椭圆的方程是
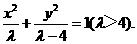
(Ⅱ)依题意,直线l的斜率存在且不为0,记为k,则直线l的方程是y=k(x-1).设点F(2,0)关于直线l的对称点为F2(x0,y0),则
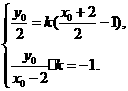 解得
解得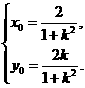
因为点F′(x0,y0)在椭圆上,所以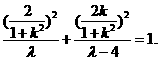 即
即
λ(λ-4)k4+2λ(λ-6)k2+(λ-4)2=0.
设k2=t,则λ(λ-4)t2+2λ(λ-6)t+(λ-4)2=0.
因为λ>4,所以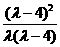 >0.
>0.
9、(北京市朝阳区2008年高三数学一模)已知椭圆W的中心在原点,焦点在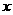 轴上,离心率为
轴上,离心率为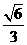 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为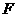 ,过左准线与
,过左准线与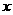 轴的交点
轴的交点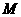 任作一条斜率不为零的直线
任作一条斜率不为零的直线 与椭圆W交于不同的两点
与椭圆W交于不同的两点 、
、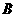 ,点
,点 关于
关于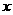 轴的对称点为
轴的对称点为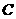 .
.
(Ⅰ)求椭圆W的方程;
(Ⅱ)求证: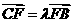 (
(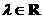 );
);
(Ⅲ)求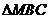 面积
面积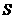 的最大值.
的最大值.
解:(Ⅰ)设椭圆W的方程为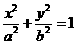 ,由题意可知
,由题意可知
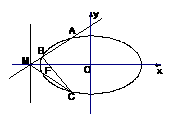
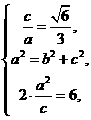 解得
解得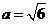 ,
,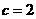 ,
,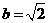 ,
,
所以椭圆W的方程为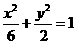 .……………………………………………4分
.……………………………………………4分
(Ⅱ)解法1:因为左准线方程为 ,所以点
,所以点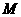 坐标为
坐标为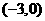 .于是可设直线
.于是可设直线 的方程为
的方程为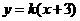 .
.
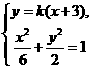 得
得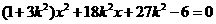 .
.
由直线 与椭圆W交于
与椭圆W交于 、
、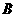 两点,可知
两点,可知
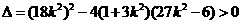 ,解得
,解得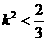 .
.
设点 ,
,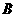 的坐标分别为
的坐标分别为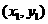 ,
,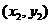 ,
,
则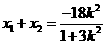 ,
,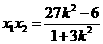 ,
,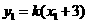 ,
,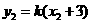 .
.
因为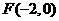 ,
, ,
,
所以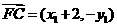 ,
,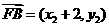 .
.
又因为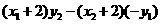
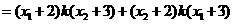
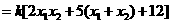
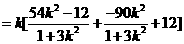
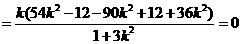 ,
,
所以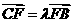 . ……………………………………………………………10分
. ……………………………………………………………10分
解法2:因为左准线方程为 ,所以点
,所以点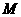 坐标为
坐标为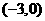 .
.
于是可设直线 的方程为
的方程为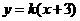 ,点
,点 ,
,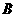 的坐标分别为
的坐标分别为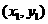 ,
,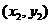 ,
,
则点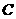 的坐标为
的坐标为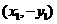 ,
,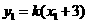 ,
,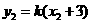 .
.
由椭圆的第二定义可得
 ,
,
所以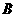 ,
,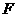 ,
,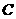 三点共线,即
三点共线,即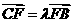 .…………………………………10分
.…………………………………10分
(Ⅲ)由题意知

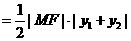
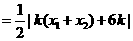
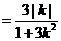
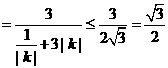 ,
,
当且仅当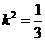 时“=”成立,
时“=”成立,
所以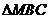 面积
面积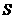 的最大值为.
的最大值为.
4、(2008江苏省启东中学高三综合测试四)已知以向量v=(1,
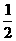 )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0, 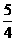 ),抛物线C:
),抛物线C: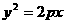 (p>0)的顶点关于直线l的对称点在该抛物线上.
(p>0)的顶点关于直线l的对称点在该抛物线上.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.
解:(Ⅰ)由题意可得直线l: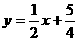 ①
①
过原点垂直于l的直线方程为
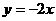 ②
②
解①②得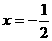 .
.
∵抛物线的顶点关于直线l的对称点在该抛物线的准线上.
∴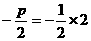 ,
,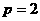
∴抛物线C的方程为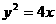 .
.
(Ⅱ)设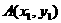 ,
,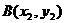 ,
,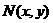 ,
,
 由
由 ,得
,得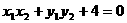 .
.
又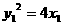 ,
,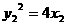 .
.
解得 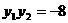 ③
③
直线ON: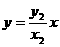 ,即
,即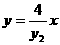 ④
④
由③、④及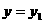 得,
得,
点N的轨迹方程为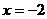
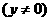 .
.
28、(福建省仙游一中2008届高三第二次高考模拟测试)已知方向向量为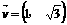 的直线
的直线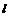 过椭圆C:=1(a>b>0)的焦点以及点(0,
过椭圆C:=1(a>b>0)的焦点以及点(0,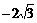 ),椭圆C的中心关于直线
),椭圆C的中心关于直线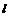 的对称点在椭圆C的右准线上。
的对称点在椭圆C的右准线上。
⑴求椭圆C的方程。
⑵过点E(-2,0)的直线 交椭圆C于点M、N,且满足
交椭圆C于点M、N,且满足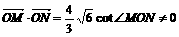 ,(O为坐标原点),求直线
,(O为坐标原点),求直线 的方程。
的方程。
解:⑴直线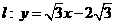 ①,过原点垂直于
①,过原点垂直于 的直线方程为
的直线方程为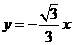 ②
②
解①②得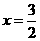 ,∵椭圆中心O(0,0)关于直线
,∵椭圆中心O(0,0)关于直线 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
∴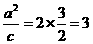 , …………………(2分)
, …………………(2分)
∵直线 过椭圆焦点,∴该焦点坐标为(2,0),∴
过椭圆焦点,∴该焦点坐标为(2,0),∴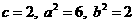 ,
,
故椭圆C的方程为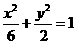 ③…………………(4分)
③…………………(4分)
⑵当直线 的斜率存在时,设
的斜率存在时,设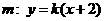 ,代入③并整理得
,代入③并整理得
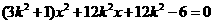 ,设
,设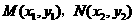 ,
,
则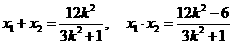 ……………(5分)
……………(5分)
∴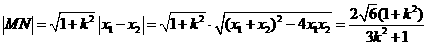 ,……(7分)
,……(7分)
点 到直线
到直线 的距离
的距离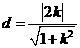 .
.
∵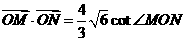 ,即
,即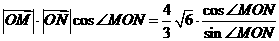 ,
,
又由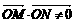 得
得  ,
,
∴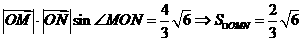 ,…………………………(9分)
,…………………………(9分)
而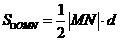 ,∴
,∴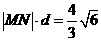 ,即
,即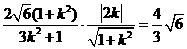 ,
,
解得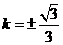 ,此时
,此时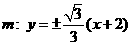 …………………………………(11分)
…………………………………(11分)
当直线 的斜率不存在时,
的斜率不存在时,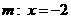 ,也有
,也有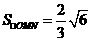 ,
,
经检验,上述直线 均满足
均满足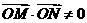 ,
,
故直线 的方程为
的方程为 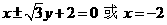
3.(2008年山东卷,理科,22)
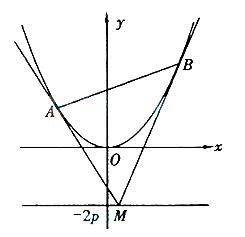 如图,设抛物线方程为
如图,设抛物线方程为 为直线
为直线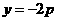 上任意一点,过
上任意一点,过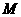 引抛物线的切线,切点分别为
引抛物线的切线,切点分别为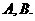
(I)求证: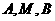 三点的横坐标成等差数列;
三点的横坐标成等差数列;
(II)已知当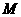 点的坐标为
点的坐标为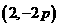 时,
时,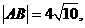 求此时抛物线的方程;
求此时抛物线的方程;
(III)是否存在点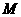 ,使得点
,使得点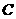 关于直线
关于直线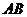 的对称点
的对称点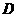 在抛物线
在抛物线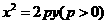 上,其中点
上,其中点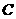 满足
满足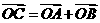 (
( 为坐标原点)。若存在,求出所有适合题意的点的坐标;若不存在,请说明理由。
为坐标原点)。若存在,求出所有适合题意的点的坐标;若不存在,请说明理由。
[答案](I)证明:由题意设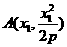 ,
,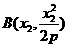 ,
,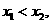
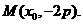
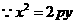 ,
,
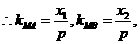
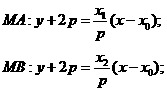

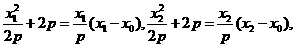
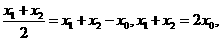
所以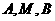 三点的横坐标成等差数列。
三点的横坐标成等差数列。
(II)解:由(I)知,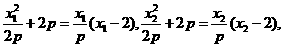
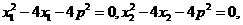
所以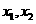 是方程
是方程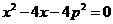 的两根,
的两根,
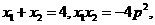
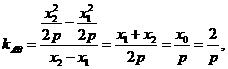
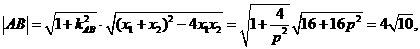
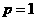 或
或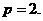
因此所求抛物线方程为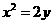 或
或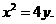
(III)解:设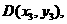 由题意得
由题意得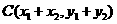 ,则
,则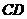 中点坐标为
中点坐标为
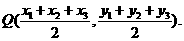
设直线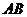 的方程为
的方程为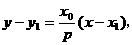
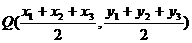 与
与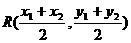 都在
都在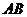 上,代入得
上,代入得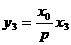 .
.
若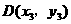 在抛物线上,则
在抛物线上,则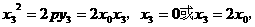 即
即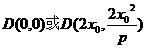 .
.
1)当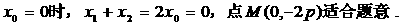
2)当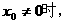
(1)对于
 矛盾.
矛盾.
(2)对于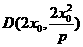 ,
,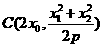 ,则
,则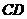 与
与 轴平行,而
轴平行,而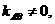 直线
直线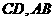 不垂直矛盾。
不垂直矛盾。
综上可知,仅存在一点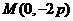 适合题意.
适合题意.
例4. 已知椭圆W的中心在原点,焦点在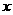 轴上,离心率为
轴上,离心率为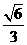 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为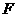 ,过左准线与
,过左准线与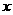 轴的交点
轴的交点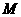 任作一条斜率不为零的直线
任作一条斜率不为零的直线 与椭圆W交于不同的两点
与椭圆W交于不同的两点 、
、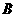 ,点
,点 关于
关于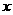 轴的对称点为
轴的对称点为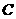 .
.
(1)求椭圆W的方程;
(2)求证: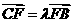 (
(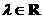 );
);
(3)求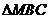 面积
面积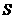 的最大值.
的最大值.
解:(1)设椭圆W的方程为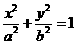 ,由题意可知
,由题意可知

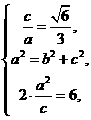 解得
解得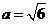 ,
,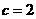 ,
,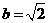 ,
,
所以椭圆W的方程为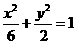 .……………………………………………4分
.……………………………………………4分
(2)解法1:因为左准线方程为 ,所以点
,所以点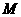 坐标为
坐标为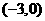 .于是可设直线
.于是可设直线 的方程为
的方程为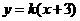 .
.
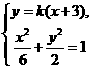 得
得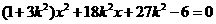 .
.
由直线 与椭圆W交于
与椭圆W交于 、
、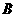 两点,可知
两点,可知
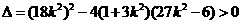 ,解得
,解得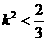 .
.
设点 ,
,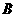 的坐标分别为
的坐标分别为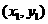 ,
,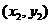 ,
,
则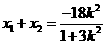 ,
,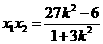 ,
,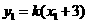 ,
,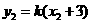 .
.
因为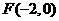 ,
, ,
,
所以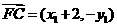 ,
,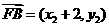 .
.
又因为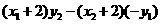
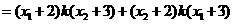
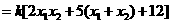
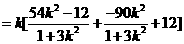
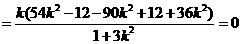 ,
,
所以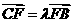 .
……………………………………………………………10分
.
……………………………………………………………10分
解法2:因为左准线方程为 ,所以点
,所以点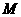 坐标为
坐标为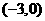 .
.
于是可设直线 的方程为
的方程为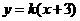 ,点
,点 ,
,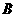 的坐标分别为
的坐标分别为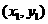 ,
,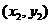 ,
,
则点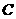 的坐标为
的坐标为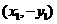 ,
,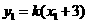 ,
,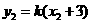 .
.
由椭圆的第二定义可得
 ,
,
所以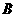 ,
,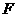 ,
,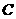 三点共线,即
三点共线,即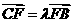 .…………………………………10分
.…………………………………10分
(3)由题意知

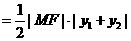
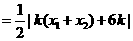
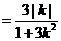
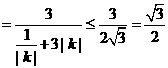 ,
,
当且仅当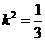 时“=”成立,
时“=”成立,
所以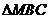 面积
面积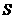 的最大值为.
的最大值为.
例4 点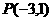 在椭圆
在椭圆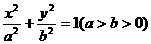 的左准线上,过点P且方向为
的左准线上,过点P且方向为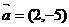 的光线经直线
的光线经直线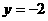 反射后通过椭圆的左焦点,则这个椭圆的离心率为( )
反射后通过椭圆的左焦点,则这个椭圆的离心率为( )
(A)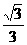 (B)
(B)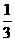 (C)
(C)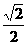 (D)
(D)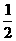
解:点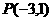 关于直线
关于直线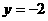 的对称点为
的对称点为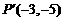 ,因为入射光线的斜率为
,因为入射光线的斜率为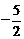 ,所以反射光线的斜率为
,所以反射光线的斜率为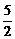 ,反射光线的方程为:
,反射光线的方程为: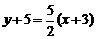 ,令
,令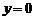 ,得
,得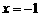 ,即
,即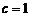 ,又
,又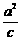
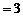 ,得
,得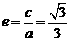 ,选A
,选A
[例3] 如下图,在双曲线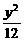 -
-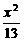 =1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.
=1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.
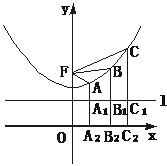
(1)求y1+y3的值;
(2)证明:线段AC的垂直平分线经过某一定点,并求此点坐标.
剖析:可以验证F为焦点,利用第二定义可得三点到准线的距离也成等差数列,进而有三点纵坐标成等差数列,由此易得y1+y3的值.为求出AC的中垂线所过定点,不妨设想作出A与C关于y轴的对称点A′与C′.由双曲线的对称性,易知A′与C′也在双曲线上,且A′、B、C′满足题设条件,所以A′C′的中垂线也应过此定点.由两条中垂线关于y轴对称.所以定点应在y轴上.
(1)解:c= =5,故F为双曲线的焦点,设准线为l,离心率为e,由题设有2|FB|=|FA|+|FC|. ①
=5,故F为双曲线的焦点,设准线为l,离心率为e,由题设有2|FB|=|FA|+|FC|. ①
分别过A、B、C作x轴的垂线AA2、BB2、CC2,交l于A1、B1、C1,则由双曲线第二定义有|FB|=e|BB1|,|FA|=e|AA1|,|FC|=e|CC1|,代入①式,得2e|BB1|=e|AA1|+e|CC1|,
即2|BB1|=|AA1|+|CC1|.
于是两边均加上准线与x轴距离的2倍,有
2|BB2|=|AA2|+|CC2|,
此即2×6=y1+y3,可见y1+y3=12.
(2)证明:AC的中垂线方程为
y-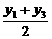 =-
=-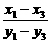 (x-
(x-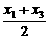 ),即y-6=-
),即y-6=-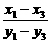 x+
x+ .
②
.
②
由于A、C均在双曲线上,所以有 -
-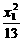 =1,
=1,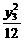 -
-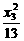 =1.
=1.
相减得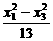 =
=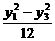 .于是有
.于是有
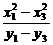 =
=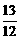 (y1+y3)=
(y1+y3)=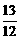 ·12=13,
·12=13,
故②变为y=-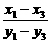 x+
x+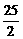 ,易知此直线过定点D(0,
,易知此直线过定点D(0,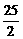 ).
).
评述:利用第二定义得焦半径,可使问题容易解决.中垂线过弦AC的中点,中点问题往往把A、C的坐标代入方程,两式相减、变形,即可解决问题.
4.(2008年湖南卷,文科,19)
已知椭圆的中心在原点,一个焦点是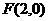 ,且两条准线间的距离为
,且两条准线间的距离为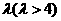 .
.
(I)求椭圆的方程;
(II)若存在过点A(1,0)的直线 ,使点F关于直线
,使点F关于直线 的对称点在椭圆上,
的对称点在椭圆上,
求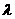 的取值范围.
的取值范围.
[解析](I)椭圆方程由a,b,c的关系易得,(II)设出直线 的方程,求出点F关于直线
的方程,求出点F关于直线 的对称点,代入椭圆方程解关于
的对称点,代入椭圆方程解关于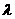 的不等式组即得
的不等式组即得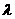 的取值范围.
的取值范围.
[答案](I)设椭圆的方程为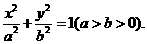
由条件知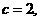 且
且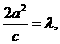 所以
所以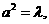
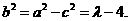
故椭圆的方程是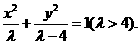
(II)依题意, 直线 的斜率存在且不为0,记为
的斜率存在且不为0,记为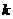 ,则直线
,则直线 的方程是
的方程是
设点 关于直线
关于直线 的对称点为
的对称点为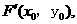 则
则
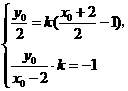 解得
解得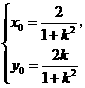
因为点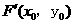 在椭圆上,所以
在椭圆上,所以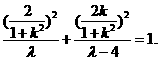 即
即
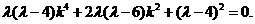
设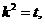 则
则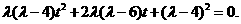
因为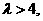 所以
所以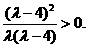 于是,
于是,
当且仅当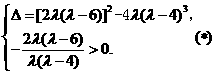
上述方程存在正实根,即直线 存在.
存在.
解 得
得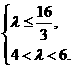 所以
所以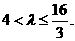
即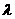 的取值范围是
的取值范围是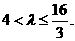
3.一束光线从点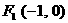 出发,经直线
出发,经直线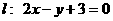 上一点
上一点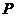 反射后,恰好穿过点
反射后,恰好穿过点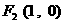 .
.
(Ⅰ)求点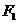 关于直线
关于直线 的对称点
的对称点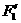 的坐标;
的坐标;
(Ⅱ)求以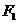 、
、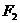 为焦点且过点
为焦点且过点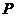 的椭圆
的椭圆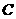 的方程;
的方程;
(Ⅲ)设直线 与椭圆
与椭圆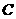 的两条准线分别交于
的两条准线分别交于 、
、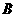 两点,点
两点,点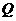 为线段
为线段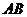 上的动点,求点
上的动点,求点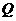 到
到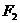 的距离与到椭圆
的距离与到椭圆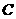 右准线的距离之比的最小值,并求取得最小值时点
右准线的距离之比的最小值,并求取得最小值时点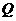 的坐标.
的坐标.
解:(Ⅰ)设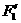 的坐标为
的坐标为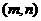 ,则
,则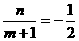 且
且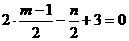 .……2分
.……2分
解得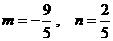 , 因此,点
, 因此,点
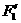 的坐标为
的坐标为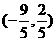 . …………………4分
. …………………4分
(Ⅱ)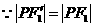 ,根据椭圆定义,
,根据椭圆定义,
得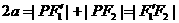
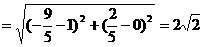 ,……………5分
,……………5分
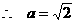 ,
,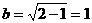 .
.
∴所求椭圆方程为 .
………………………………7分
.
………………………………7分
(Ⅲ)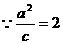 ,
, 椭圆的准线方程为
椭圆的准线方程为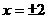 .
…………………………8分
.
…………………………8分
设点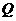 的坐标为
的坐标为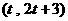
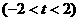 ,
,
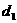 表示点
表示点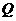 到
到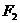 的距离,
的距离,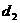 表示点
表示点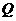 到椭圆的右准线的距离.
到椭圆的右准线的距离.
则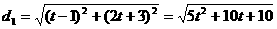 ,
,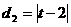 .
.
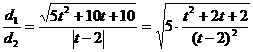 ,
……………………………10分
,
……………………………10分
令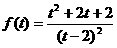
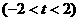 ,则
,则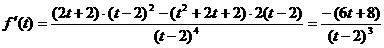 ,
,
 当
当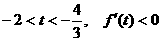 ,
,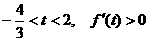 ,
,
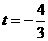 ,
, .
.
∴ 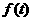 在
在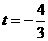 时取得最小值.
………………………………13分
时取得最小值.
………………………………13分
因此,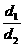 最小值=
最小值=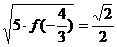 ,此时点
,此时点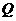 的坐标为
的坐标为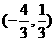 .…………14分
.…………14分
注: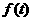 的最小值还可以用判别式法、换元法等其它方法求得.
的最小值还可以用判别式法、换元法等其它方法求得.
说明:求得的点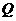
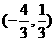 即为切点
即为切点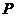 ,
,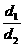 的最小值即为椭圆的离心率.
的最小值即为椭圆的离心率.
1.若抛物线y=2x2上的两点A(x1,y1)、B(x2,y2)关于直线y=x+m对称且x1x2=-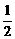 ,求m的值.
,求m的值.
解:设直线AB的方程为y=-x+b,代入y=2x2得2x2+x-b=0,
∴x1+x2=-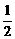 ,x1x2=
,x1x2= =-
=-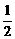 .
.
∴b=1,即AB的方程为y=-x+1.
设AB的中点为M(x0,y0),则
x0=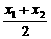 =-
=-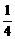 ,代入y0=-x0+1,
,代入y0=-x0+1,
得y0=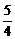 .又M(-
.又M(-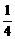 ,
,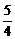 )在y=x+m上,
)在y=x+m上,
∴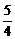 =-
=-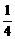 +m.∴m=
+m.∴m=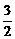 .
.
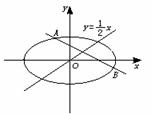
[例2]过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为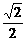 的椭圆C相交于A、B两点,直线y=
的椭圆C相交于A、B两点,直线y=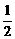 x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
解法一:由e=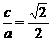 ,得
,得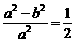 ,从而a2=2b2,c=b.
,从而a2=2b2,c=b.
设椭圆方程为x2+2y2=2b2,A(x1,y1),B(x2,y2)在椭圆上.
则x12+2y12=2b2,x22+2y22=2b2,两式相减得,(x12-x22)+2(y12-y22)=0,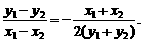
设AB中点为(x0,y0),则kAB=-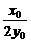 ,又(x0,y0)在直线y=
,又(x0,y0)在直线y=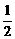 x上,y0=
x上,y0=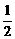 x0,于是-
x0,于是-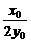 =
=
-1,kAB=-1,设l的方程为y=-x+1.
右焦点(b,0)关于l的对称点设为(x′,y′),

由点(1,1-b)在椭圆上,得1+2(1-b)2=2b2,b2=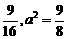 .
.
∴所求椭圆C的方程为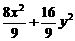 =1,l的方程为y=-x+1.
=1,l的方程为y=-x+1.
解法二:由e=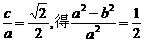 ,从而a2=2b2,c=b.
,从而a2=2b2,c=b.
设椭圆C的方程为x2+2y2=2b2,l的方程为y=k(x-1),
将l的方程代入C的方程,得(1+2k2)x2-4k2x+2k2-2b2=0,则x1+x2=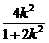 ,y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=-
,y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=-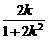 .
.
直线l:y=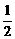 x过AB的中点(
x过AB的中点(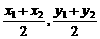 ),则
),则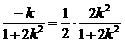 ,解得k=0,或k=-1.
,解得k=0,或k=-1.
若k=0,则l的方程为y=0,焦点F(c,0)关于直线l的对称点就是F点本身,不能在椭圆C上,所以k=0舍去,从而k=-1,直线l的方程为y=-(x-1),即y=-x+1,以下同解法一.
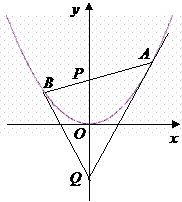
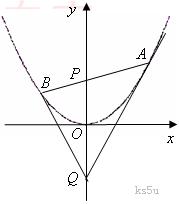 2如图,过抛物线
2如图,过抛物线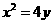 的对称轴上任一点
的对称轴上任一点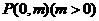 作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点
作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点
⑴.设点P满足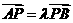 (
(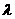 为实数),
为实数),
证明: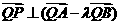 ;
;
⑵.设直线AB的方程是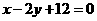 ,过A、B两点
,过A、B两点
的圆C与抛物线在点A处有共同的切线,求圆C的方程.
解⑴.依题意,可设直线AB的方程为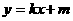 ,代入抛物线方程
,代入抛物线方程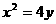 ,得:
,得:
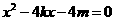 ① …………………………………………………………… 2分
① …………………………………………………………… 2分
设A、B两点的坐标分别是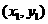 、
、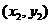 ,则
,则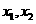 是方程①的两根,
是方程①的两根,
所以,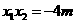 . ……………………………………………………………………… 3分
. ……………………………………………………………………… 3分
由点P满足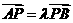 (
(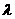 为实数,
为实数,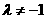 ),得
),得 ,
即
,
即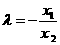 .
.
 又点Q是点P关于原点的以称点,故点Q的坐标是
又点Q是点P关于原点的以称点,故点Q的坐标是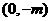 ,从而
,从而 .
.
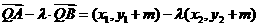
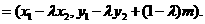
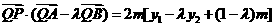
=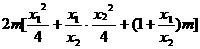
=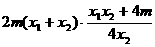
=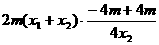 =0 ………………………… 6分
=0 ………………………… 6分
所以,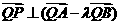 . ………………………………………………………………… 7分
. ………………………………………………………………… 7分
⑵.由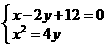 得点A、B的坐标分别是
得点A、B的坐标分别是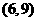 、
、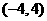 .
.
由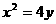 得
得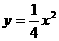 ,
,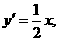
所以,抛物线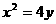 在点A处切线的斜率为
在点A处切线的斜率为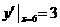 .
………………
9分
.
………………
9分
设圆C的方程是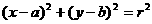 ,
,
则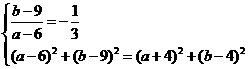 ……………………… 11分
……………………… 11分
解得: .…………………………… 13分
.…………………………… 13分
所以,圆C的方程是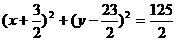 . ………………………… 14分
. ………………………… 14分
排列、组合和二项式定理
⑴排列数公式: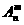 =n(n-1)(n-2)…(n-m+1)=
=n(n-1)(n-2)…(n-m+1)=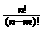 (m≤n,m、n∈N*),当m=n时为全排列
(m≤n,m、n∈N*),当m=n时为全排列 =n(n-1)(n-2)…3.2.1=n!;
=n(n-1)(n-2)…3.2.1=n!;
⑵组合数公式: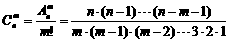 (m≤n),
(m≤n),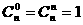 ;
;
⑶组合数性质: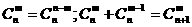 ;
;
⑷二项式定理: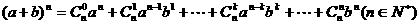
①通项: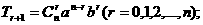 ②注意二项式系数与系数的区别;
②注意二项式系数与系数的区别;
⑸二项式系数的性质:
①与首末两端等距离的二项式系数相等;②若n为偶数,中间一项(第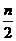 +1项)二项式系数最大;若n为奇数,中间两项(第
+1项)二项式系数最大;若n为奇数,中间两项(第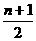 和
和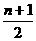 +1项)二项式系数最大;
+1项)二项式系数最大;
③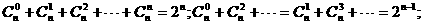
(6)求二项展开式各项系数和或奇(偶)数项系数和时,注意运用赋值法。
2. 概率与统计
⑴随机变量的分布列:①随机变量分布列的性质:pi≥0,i=1,2,…; p1+p2+…=1;
②离散型随机变量:
|
X |
x1 |
X2 |
… |
xn |
… |
|
P |
P1 |
P2 |
… |
Pn |
… |
期望:EX= x1p1 + x2p2 + … + xnpn + … ;
方差:DX=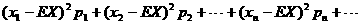 ;
;
注: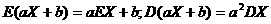 ;
;
③二项分布(独立重复试验):
若X-B(n,p),则EX=np, DX=np(1- p);注: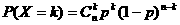 。
。
⑵条件概率:称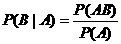 为在事件A发生的条件下,事件B发生的概率。
为在事件A发生的条件下,事件B发生的概率。
注:①0 P(B|A)
P(B|A) 1;②P(B∪C|A)=P(B|A)+P(C|A)。
1;②P(B∪C|A)=P(B|A)+P(C|A)。
⑶独立事件同时发生的概率:P(AB)=P(A)P(B)。
⑷正态总体的概率密度函数: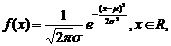 式中
式中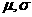 是参数,分别表示总体的平均数(期望值)与标准差;
是参数,分别表示总体的平均数(期望值)与标准差;
(6)正态曲线的性质:
①曲线位于x轴上方,与x轴不相交;②曲线是单峰的,关于直线x=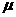 对称;
对称;
③曲线在x=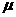 处达到峰值
处达到峰值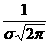 ;④曲线与x轴之间的面积为1;
;④曲线与x轴之间的面积为1;
当 一定时,曲线随
一定时,曲线随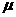 质的变化沿x轴平移;
质的变化沿x轴平移;
当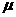 一定时,曲线形状由
一定时,曲线形状由 确定:
确定: 越大,曲线越“矮胖”,表示总体分布越集中;
越大,曲线越“矮胖”,表示总体分布越集中;
 越小,曲线越“高瘦”,表示总体分布越分散。
越小,曲线越“高瘦”,表示总体分布越分散。
注:P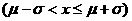 =0.6826;P
=0.6826;P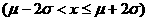 =0.9544
=0.9544
P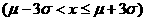 =0.9974
=0.9974
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com