
题目列表(包括答案和解析)
4.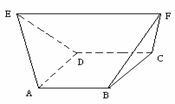 (2005年全国Ⅰ高考题)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为
(2005年全国Ⅰ高考题)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为
A.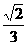 B.
B.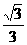
C.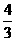 D.
D.
3.设三棱柱ABC-A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B-APQC的体积为
A. B. C. D.
2..(2005年全国Ⅰ高考题)一个与球心距离为1的平面截球所得的圆面面积为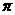 ,则球的表面积为
,则球的表面积为
A.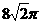 B.
B.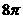 C.
C.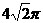 D.
D.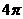
只有一项是符合题目要求的.
1.(2005年全国Ⅰ高考题)过三棱柱任意两个顶点的直线共15条,其中异面直线有
A.18对 B.24对 C.30对 D.36对
27. 解:(Ⅰ)由题意,c=1,可设椭圆方程为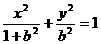
因为A在椭圆上,所以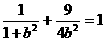 ,解得
,解得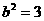 ,
,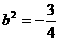 (舍去)
(舍去)
所以椭圆方程为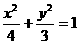 。
。
(Ⅱ)设直线AE方程为: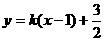 ,代入
,代入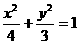 得
得
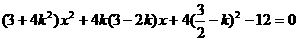
设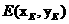 ,
,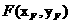 ,因为点
,因为点 在椭圆上,所以
在椭圆上,所以
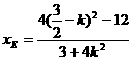
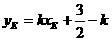
又直线AF的斜率与AE的斜率互为相反数,在上式中以-K代K,可得

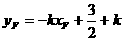
所以直线EF的斜率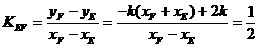
即直线EF的斜率为定值,其值为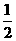 。
。
26. 解:(1)由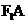 //
//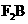 且
且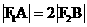 ,得
,得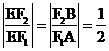 ,从而
,从而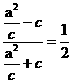
整理,得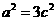 ,故离心率
,故离心率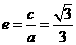
(2)解:由(1)得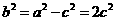 ,所以椭圆的方程可写为
,所以椭圆的方程可写为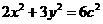
设直线AB的方程为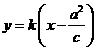 ,即
,即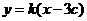 .
.
由已知设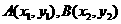 ,则它们的坐标满足方程组
,则它们的坐标满足方程组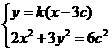
消去y整理,得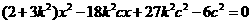
依题意,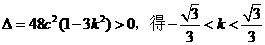
而 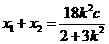 ①
①
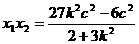 ②
②
由题设知,点B为线段AE的中点,所以
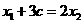 ③
③
联立①③解得
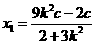 ,
,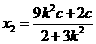
将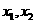 代入②中,解得
代入②中,解得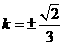 .
.
(3)解法一:由(II)可知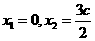
当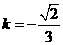 时,得
时,得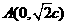 ,由已知得
,由已知得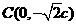 .
.
线段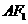 的垂直平分线
的垂直平分线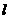 的方程为
的方程为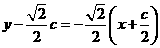 直线
直线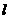 与x轴的交点
与x轴的交点
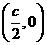 是
是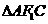 外接圆的圆心,因此外接圆的方程为
外接圆的圆心,因此外接圆的方程为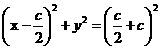 .
.
直线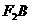 的方程为
的方程为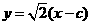 ,于是点H(m,n)的坐标满足方程组
,于是点H(m,n)的坐标满足方程组
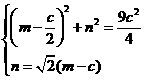 , 由
, 由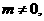 解得
解得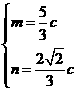 故
故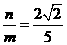
当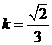 时,同理可得
时,同理可得 .
.
解法二:由(II)可知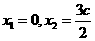
当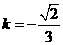 时,得
时,得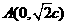 ,由已知得
,由已知得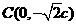
由椭圆的对称性可知B,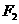 ,C三点共线,因为点H(m,n)在
,C三点共线,因为点H(m,n)在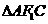 的外接圆上,
的外接圆上,
且 ,所以四边形
,所以四边形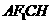 为等腰梯形.
为等腰梯形.
由直线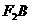 的方程为
的方程为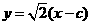 ,知点H的坐标为
,知点H的坐标为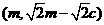 .
.
因为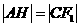 ,所以
,所以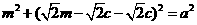 ,解得m=c(舍),或
,解得m=c(舍),或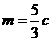 .
.
则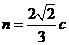 ,所以
,所以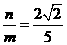 .
.
当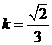 时,同理可得
时,同理可得
25. 解:(1)∵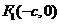 ,∴
,∴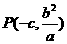 .∵OP∥AB,∴
.∵OP∥AB,∴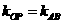 ,∴
,∴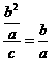 ,
,
解得:b=c.∴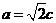 ,故
,故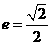 .
.
(2)由(1)知椭圆方程可化简为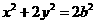 .①
.①
易求直线QR的斜率为 ,故可设直线QR的方程为:
,故可设直线QR的方程为: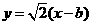 .②
.②
由①②消去y得: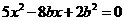 .∴
.∴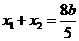 ,
,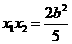 .
.
于是△ 的面积S=
的面积S=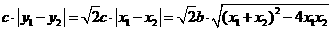
=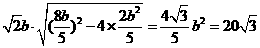 ,∴
,∴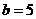 .
.
因此椭圆的方程为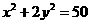 ,即
,即 .
.
24. 解:(1)

(2)

23. 解:(1)在曲线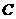 上任取一个动点P(x,
y),
上任取一个动点P(x,
y),
则点(x,2y)在圆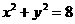 上.
上.
所以有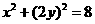 . 整理得曲线C的方程为
. 整理得曲线C的方程为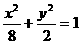 .
.
(2)∵直线 平行于OM,且在y轴上的截距为m,又
平行于OM,且在y轴上的截距为m,又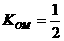 ,
,
∴直线 的方程为
的方程为 .
.
由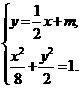 , 得
, 得 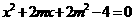
∵直线 与椭圆交于A、B两个不同点,
与椭圆交于A、B两个不同点,
∴
解得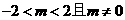 .
.
∴m的取值范围是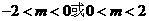 .
.
22. 解:(Ⅰ)因为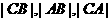 成等差数列,点
成等差数列,点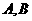 的坐标分别为
的坐标分别为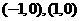
所以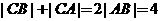 且
且
由椭圆的定义可知点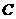 的轨迹是以
的轨迹是以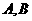 为焦点长轴为4的椭圆(去掉长轴的端点),
为焦点长轴为4的椭圆(去掉长轴的端点),
所以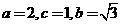 .
.
故顶点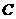 的轨迹
的轨迹 方程为
方程为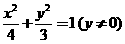
(Ⅱ)由题意可知直线 的斜率存在,设直线
的斜率存在,设直线 方程为
方程为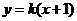 .
.
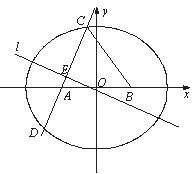
由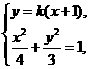 得
得
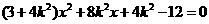 ,
,
设 两点坐标分别为
两点坐标分别为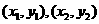 ,
,
则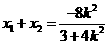 ,
,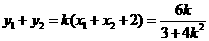 ,
,
所以线段 中点
中点 的坐标为
的坐标为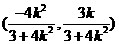 ,
,
故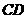 垂直平分线
垂直平分线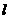 的方程为
的方程为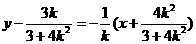 ,
,
令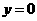 ,得
,得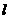 与
与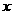 轴交点的横坐标为
轴交点的横坐标为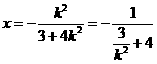 ,
,
由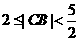 得
得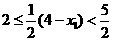 ,解得
,解得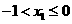 ,
,
又因为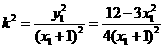 ,所以
,所以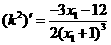 .
.
当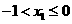 时,有
时,有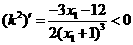 ,此时函数
,此时函数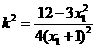 递减,
递减,
所以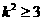 .所以,
.所以,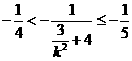 .
.
故直线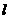 与
与 轴交点的横坐标的范围是
轴交点的横坐标的范围是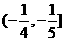 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com