
题目列表(包括答案和解析)
7.(2009·惠州模拟)若点P(m,n) (n≠0)为角600°终边上一点,则=________.
解析 由三角函数的定义知
=tan 600°=tan(360°+240°)=tan 240°=tan 60°=,
∴==.
答案
6.(2009·湘潭联考)已知α是第一象限角,tan α=,则sin α等于 ( )
A. B. C.- D.-
解析 由,得sin α=(sin α>0).
答案 B
5.(2010·新乡模拟)已知角α是第二象限角,且|cos |=-cos ,则角是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
解析 由α是第二象限角知,是第一或第三象限角.
又∵=-cos ,∴cos <0,
∴是第三象限角.
答案 C
4.(2009·衢州模拟)已知角α的终边过点P(-8m,-6sin 30°),且cos α=-,则m的值为( )
A.- B. C.- D.
解析 r=,
∴cos α==-,∴m>0,
∴=,∴m=±.∵m>0,∴m=.
答案 B
3.(2010·漳州调研)若扇形圆心角的弧度数为2,且扇形弧所对的弦长也是2,则这个扇形的
面积为 ( )
A. B. C. D.
解析 由题意得扇形的半径为.又由扇形面积公式得,该扇形的面积为·2·=.
答案 A
2.(2010·湛江调研)已知点P(tan α,cos α)在第三象限,则角α的终边在第几象限( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析 ∵P(tan α,cos α)在第三象限,∴,
由tan α<0,得α在第二、四象限,
由cos α<0,得α在第二、三象限
∴α在第二象限.
答案 B
1.(2009·汕头模拟)若角α和角β的终边关于x轴对称,则角α可以用角β表示为( )
A.2kπ+β (k∈Z) B.2kπ-β (k∈Z)
C.kπ+β (k∈Z) D.kπ-β (k∈Z)
解析 因为角α和角β的终边关于x轴对称,所以α+β=2kπ (k∈Z).所以α=2kπ-β (k∈Z).
答案 B
18.(10分) 已知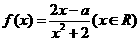 在区间
在区间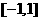 上是增函数。
上是增函数。
(Ⅰ)求实数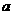 的值所组成的集合
的值所组成的集合 ;
;
(Ⅱ)设关于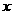 的方程
的方程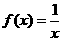 的两个根为
的两个根为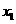 、
、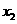 ,若对任意
,若对任意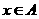 及
及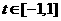 ,不等式
,不等式
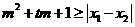 恒成立,求
恒成立,求 的取值范围.
的取值范围.
17.(本小题满分10分) 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
16. 甲、乙两地相距S(千米),汽车从甲地匀速行驶到乙地,速度最大不得超过c(千米/小时).已知汽车每小时的运输成本(元)由可变部分与固定部分组成.可变部分与速度v(千米/小时)的平方成正比,且比例系数为正常数b;固定部分为a元.
(1) 试将全程运输成本Y(元)表示成速度V(千米/小时)的函数.
(2) 为使全程运输成本最省,汽车应以多大速度行驶?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com