10．(13分)(2009·周口调研)已知函数f(x)=Asin(ωx+φ)+

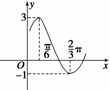
b (ω>0，|φ|<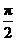)的图象的一部分如图所示：

(1)求f(x)的表达式；

(2)试写出f(x)的对称轴方程．

解　(1)由图象可知，函数的最大值M=3，

最小值m=-1，则A=，

又，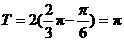

∴，∴f(x)=2sin(2x+φ)+1，

将x=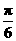，y=3代入上式，得，

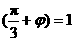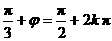∴，k∈Z，

即φ=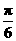+2kπ，k∈Z，∴φ=，

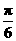∴f(x)=2sin+1.

(2)由2x+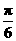=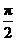+kπ，得x=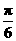+kπ，k∈Z，

∴f(x)=2sin+1的对称轴方程为

kπ，k∈Z.

9．(2009·云浮期末)若函数f(x)＝2sin ωx (ω>0)在上单调递增，则ω的最大值为

________．

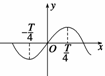解析　∵f(x)在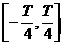上递增，

故

即≥.∴ω≤.∴ω_max=.

答案　

8．(2008·全国Ⅱ改编)若动直线x＝a与函数f(x)＝sin x和g(x)＝cos x的图象分别交于M、N

两点，则|MN|的最大值为________．

解析　设x＝a与f(x)＝sin x的交点为M(a，y₁)，

x＝a与g(x)＝cos x的交点为N(a，y₂)，

则|MN|＝|y₁－y₂|＝|sin a－cos a|

＝≤.

答案　

7．(2009·江苏，4)函数y=Asin(ωx+φ)(A、ω、φ为常数，

A>0，ω>0)在闭区间[-π，0]上的图象如图所示，则ω=

　　　 　.

解析　由函数y=Asin(ωx+φ)的图象可知：

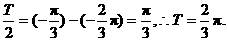
答案　3

6．(2009·天津理，7)已知函数f(x)＝sin(ωx+)(x∈R，ω>0)的最小正周期为π，为了得到函数g(x)＝cos ωx的图象，只要将y＝f(x)的图象　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　 (　)

A．向左平移个单位长度

B．向右平移个单位长度

C．向左平移个单位长度

D．向右平移个单位长度

解析　因为T＝π，则ω＝＝2，f(x)＝sin，

g(x)＝cos 2x，将y＝f(x)的图象向左平移个单位长度时，y＝sin＝sin＝

cos 2x.

答案　A

5．(2009·杭州一模)电流强度I(安)随时间t(秒)变化的函数

I=Asin(ωt+φ)(A>0，ω>0,0<φ<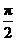)的图象如右图所示，

则当t=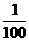秒时，电流强度是　　　　　　　　　　　　　　　　　 (　)

A．－5安　 　　　　　　　　　　 B．5安 　　　　　　　 　C．5安 　　　　　　　　 　D．10安

解析　由图象知A＝10，＝－＝，

∴ω＝＝100π.∴I＝10sin(100πt+φ)．

为五点中的第二个点，∴100π×+φ＝.

∴φ＝.∴I＝10sin，

当t＝秒时，I＝－5安．

答案　A

4．(2009·全国Ⅱ文，9)若将函数y＝tan(ω>0)的图象向右平移个单位长度后，与函数y＝tan的图象重合，则ω的最小值为　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　 B.　 　　　　　　　　　　　　　 C.　 　　　　　　　　　　　　　 D.

解析　函数y＝tan向右平移后得到

解析y＝tan＝tan.又因为y＝tan，∴令－＝+kπ，∴＝+kπ(k∈Z)，由ω>0得ω的最小值为.

答案　D

3．(2010·莱芜一模)若函数y＝Asin(ωx+φ)+m的最大值为4，最小值为0，最小正周期为，

直线x＝是其图象的一条对称轴，则它的解析式是　　　　　　　　　　　　　　　　　　　　　　 (　)

A．y＝4sin　 　　　　　　　　　　　　　　　　　 B．y＝2sin+2

C．y＝2sin+2　 　　　　　　　　　　　　　　　 D．y＝2sin+2

解析　∵　∴

∵T＝，∴ω＝＝4.∴y＝2sin(4x+φ)+2.

∵x＝是其对称轴，∴sin＝±1.

∴+φ＝+kπ (k∈Z)．

∴φ＝kπ－ (k∈Z)．当k＝1时，φ＝.

答案　D

2．(2010·泉州模拟)将函数y＝sin的图象上各点的纵坐标不变，横坐标伸长到原来的2倍，再向右平移个单位，所得到的图象解析式是　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．f(x)＝sin x　 　　　　　　　　　　　　　　　　　　　　　　　　 B．f(x)＝cos x

C．f(x)＝sin 4x　 　　　　　　　　　　　　　　　　　　　　 D．f(x)＝cos 4x

解析　 y＝sin→y＝sin

→y＝sin＝sin x.

答案　A

1．(2009·山东文，3)将函数y＝sin 2x的图象向左平移个单位，再向上平移1个单位，所得

图象的函数解析式是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．y＝2cos²x　 　　　　　　　　　　　　　　　　　　　　　 B．y＝2sin²x

C．y＝1+sin(2x+)　 　　　　　　　　　　　　　　　　 D．y＝cos 2x

解析　将函数y＝sin 2x的图象向左平移个单位，得到函数y＝sin2(x+)，即y＝sin(2x+)＝cos 2x的图象，再向上平移1个单位，所得图象的函数解析式为y＝1+cos 2x＝2cos²x.

答案　A