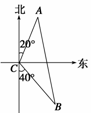
3．(2009·六安期末)如图所示，已知两座灯塔A和B与海洋观察站

C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔

B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为(　)

A．a km　 　　　　　　　　　　　　　　　　　　　　　　　　　 B.a km

C.a km　 　　　　　　　　　　　　　　　　　　　　　　　　 D．2a km

解析　利用余弦定理解△ABC.易知∠ACB＝120°，在△ABC中，由余弦定理得AB²＝AC²

+BC²－2AC·BCcos 120°＝2a²－2a²×＝3a²，∴AB＝a.

答案　B

2．(2010·池州模拟)一船向正北航行，看见正西方向有相距10海里的两个灯塔恰好与它在一

条直线上，继续航行半小时后，看见一灯塔在船的南偏西60°，另一灯塔在船的南偏西75°，

则这艘船的速度是每小时　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．5海里　 　　　　　　　　　　　　　　　　　　　　　　　　 B．5海里

C．10海里　 　　　　　　　　　　　　　　　　　　　　　　　 D．10海里

解析　如图所示，依题意有∠BAC＝60°，∠BAD＝75°，

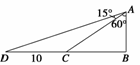所以∠CAD＝∠CDA＝15°，从而CD＝CA＝10，

在Rt△ABC中，得AB＝5，

于是这艘船的速度是＝10(海里/小时)．

答案　C

1．(2010·佛山模拟)在200 m高的山顶上，测得山下一塔顶与塔底的俯角分别是30°，60°，则塔高为　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A. m　 　　　　　　　 B. m 　　　　　　　　 　C. m　　　　　　　　 　 D. m

解析　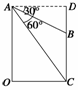作出示意图如图，

由已知：在Rt△OAC中，

OA=200，∠OAC=30°，

则OC=OA·tan∠OAC

=200tan 30°=.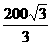

在Rt△ABD中，AD=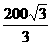，∠BAD=30°，

则BD=AD·tan∠BAD=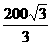·tan 30°=，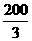

∴BC=CD-BD=200-=.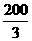

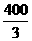答案　A

整理，得4cos²C－4cos C+1＝0，解得cos C＝，

∵0°<C<180°，∴C＝60°.

(2)由余弦定理得c²＝a²+b²－2abcos C，

即7＝a²+b²－ab，∴7＝(a+b)²－3ab，

由条件a+b＝5，得7＝25－3ab，ab＝6，

∴S_△ABC＝absin C＝×6×＝.

§4.7　正弦定理、余弦定理应用举例

12．(14分)(2010·广东五校联考)在△ABC中，角A、B、C的对边分别为a、b、c，已知a+b＝5，c＝，且4sin²－cos 2C＝.

(1)求角C的大小；

(2)求△ABC的面积．

解　(1)∵A+B+C＝180°，

由4sin²－cos 2C＝，

得4cos²－cos 2C＝，

11．(13分)(2010·芜湖模拟)在△ABC中，角A、B、C所对边长分别为a、b、c，设a、b、c

满足条件b²+c²－bc＝a²和＝+，求角A和tan B的值．

解　由b²+c²－bc＝a²，得＝，

即cos A＝，又0<A<π，∴A＝.

又＝+，＝+，

C＝π－A－B＝－B，

∴sin＝sin B，

整理得cos B+sin B＝sin B+sin B.

∴cos B＝sin B，则tan B＝.

10．(13分)(2009·淮南调研)在△ABC中，若＝，试判断△ABC的形状．

解　由已知＝＝＝，

所以＝.

方法一　利用正弦定理边化角．

由正弦定理，得＝，所以＝，

即sin Ccos C＝sin Bcos B，即sin 2C＝sin 2B.

因为B、C均为△ABC的内角，

所以2C＝2B或2C+2B＝180°，

所以B＝C或B+C＝90°，

所以△ABC为等腰三角形或直角三角形．

方法二　由余弦定理，得＝，

即(a²+b²－c²)c²＝b²(a²+c²－b²)，

所以a²c²－c⁴＝a²b²－b⁴，

即a²b²－a²c²+c⁴－b⁴＝0，

所以a²(b²－c²)+(c²－b²)(c²+b²)＝0，

即(b²－c²)(a²－b²－c²)＝0，

所以b²＝c²或a²－b²－c²＝0，

即b＝c或a²＝b²+c².

所以△ABC为等腰三角形或直角三角形．

9．(2010·中山一模)在△ABC中，角A，B，C所对的边分别为a，b，c，若其面积S＝(b²+c²－a²)，则∠A＝________.

解析　S＝(b²+c²－a²)＝(2bccos A)＝bccos A，

又S_△ABC＝bcsin A，∴sin A＝cos A，

即tan A＝1.又A为△ABC的内角，∴A＝.

答案　

8．(2009·泰安调研)在△ABC中，AB＝2，AC＝，BC＝1+，AD为边BC上的高，则AD的长是________．

解析　cos C＝＝，∴sin C＝.

∴S_△ABC＝absin C＝a×AD.∴AD＝.

答案　

7．(2009·上海春招)在△ABC中，若AB＝3，∠ABC＝75°，∠ACB＝60°，则BC＝________.

解析　根据三角形内角和定理知

∠BAC＝180°－75°－60°＝45°.

根据正弦定理得＝，

即＝，∴BC＝＝＝.

答案