
题目列表(包括答案和解析)
5.(2010·舟山一模)已知sin=,则cos的值是 ( )
A.- B.- C. D.
解析 cos=-cos
=-cos=-=-.
答案 A
4.(2009·济宁模拟)已知向量a=,b=(4,4cos α-),若a⊥b,则sin
等于 ( )
A.- B.- C. D.
解析 a·b=4sin+4cos α-
=2sin α+6cos α-=4sin-=0,
∴sin=.
∴sin=-sin=-.
答案 B
3.(2010·阳江一模)已知cos=,则sin2-cos的值是 ( )
A. B.-
C. D.
解析 sin2-cos
=1-cos2+cos=.
答案 A
2.(2009·岳阳调研)已知sin(45°+α)=,则sin 2α等于 ( )
A.- B.- C. D.
解析 sin(α+45°)=(sin α+cos α)·=,
∴sin α+cos α=.
两边平方,得1+sin 2α=.∴sin 2α=-.
答案 B
1.(2010·青岛模拟)sin 45°·cos 15°+cos 225°·sin 15°的值为 ( )
A.- B.- C. D.
解析 原式=sin 45°·cos 15°-cos 45°·sin 15°
=sin 30°=.
答案 C
12.(14分)(2009·金华模拟)已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<,x∈R)的图象的一部分如图所示.
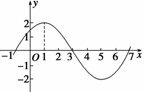
(1)求函数f(x)的解析式;
(2)当x∈时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
解 (1)由图象知A=2,T=8,
∵T==8,∴ω=.
又图象过点(-1,0),∴2sin=0.
∵|φ|<,∴φ=.
∴f(x)=2sin.
(2)y=f(x)+f(x+2)
=2sin+2sin
=2sin=2cos x.
∵x∈,∴-≤x≤-.
∴当x=-,即x=-时,y=f(x)+f(x+2)取得最大值;
当x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2.
§4.5 两角和与差的正弦、余弦和正切

11.(13分)(2009·合肥联考)函数y=Asin(ωx+φ) (A>0,ω>0,|φ|<)的一段图象如图所示.
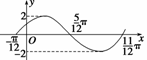
(1)求函数y=f(x)的解析式;
(2)将函数y=f(x)的图象向右平移个单位,得到y=g(x)的图象,求直线y=与函数y=f(x)+g(x)的图象在(0,π)内所有交点的坐标.
解 (1)由题图知A=2,T=π,于是ω==2,
将y=2sin 2x的图象向左平移个单位长度,
得y=2sin(2x+φ)的图象.
于是φ=2×=,∴f(x)=2sin.
(2)依题意得g(x)=2sin
=-2cos.
故y=f(x)+g(x)=2sin-2cos
=2sin.
由2sin=,得sin=.
∵0<x<π,∴-<2x-<2π-.
∴2x-=或2x-=,
∴x=π或x=π,
∴所求交点坐标为或.
10.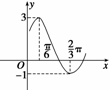 (13分)(2009·周口调研)已知函数f(x)=Asin(ωx+φ)+
(13分)(2009·周口调研)已知函数f(x)=Asin(ωx+φ)+
b (ω>0,|φ|<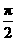 )的图象的一部分如图所示:
)的图象的一部分如图所示:
(1)求f(x)的表达式;
(2)试写出f(x)的对称轴方程.
解 (1)由图象可知,函数的最大值M=3,
最小值m=-1,则A=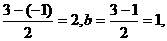 ,
,
又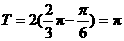 ,
,
∴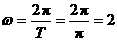 ,∴f(x)=2sin(2x+φ)+1,
,∴f(x)=2sin(2x+φ)+1,
将x=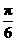 ,y=3代入上式,得
,y=3代入上式,得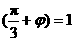 ,
,
∴ ,k∈Z,
,k∈Z,
即φ=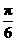 +2kπ,k∈Z,∴φ=
+2kπ,k∈Z,∴φ=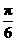 ,
,
∴f(x)=2sin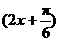 +1.
+1.
(2)由2x+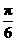 =
=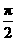 +kπ,得x=
+kπ,得x=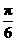 +
+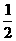 kπ,k∈Z,
kπ,k∈Z,
∴f(x)=2sin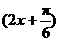 +1的对称轴方程为
+1的对称轴方程为
 kπ,k∈Z.
kπ,k∈Z.
9.(2009·云浮期末)若函数f(x)=2sin ωx (ω>0)在上单调递增,则ω的最大值为
________.
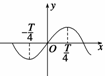 解析 ∵f(x)在
解析 ∵f(x)在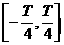 上递增,
上递增,
故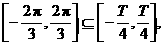
即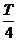 ≥
≥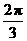 .∴ω≤
.∴ω≤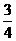 .∴ωmax=
.∴ωmax=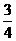 .
.
答案 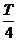
8.(2008·全国Ⅱ改编)若动直线x=a与函数f(x)=sin x和g(x)=cos x的图象分别交于M、N
两点,则|MN|的最大值为________.
解析 设x=a与f(x)=sin x的交点为M(a,y1),
x=a与g(x)=cos x的交点为N(a,y2),
则|MN|=|y1-y2|=|sin a-cos a|
=≤.
答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com