8．(2009·福建理，14)若曲线f(x)＝ax⁵+ln x存在垂直于y轴的切线，则实数a的取值范围是

________．

解析　∵f′(x)＝5ax⁴+，x∈(0，+∞)，

∴由题知5ax⁴+＝0在(0，+∞)上有解．

即a＝－在(0，+∞)上有解．

∵x∈(0，+∞)，∴－∈(－∞，0)．

∴a∈(－∞，0)．

答案　(－∞，0)

7.(2010·厦门调研)如图所示，函数f(x)的图象是折线段

ABC，其中A，B，C的坐标分别为(0，4)，(2，0)，(6，4)，

则f(f(0))=　　　　 ；0 ＝________.

(用数字作答)

解析　由A(0,4)，B(2,0)可得线段AB所在直线的方程为f(x)＝－2x+4 (0≤x≤2)．同理BC

所在直线的方程为f(x)＝x－2 (2<x≤6)．

所以f(x)＝

所以f(0)＝4，f(4)＝2.

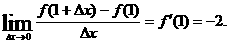
答案　2　－2

6．(2009·安徽文，9)设函数f(x)＝x³+x²+tan θ，其中θ∈，则导数f′(1)

的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．[－2,2]　 　　　　　　　　　　　　　　　　　　　　　　　 B．[，]

C．[，2]　 　　　　　　　　　　　　　　　　　　　　　　　 D．[，2]

解析　由已知f′(x)＝sin θ·x²+cos θ·x，

∴f′(1)＝sin θ+cos θ＝2sin，

又θ∈.∴≤θ+≤，

∴≤sin≤1，∴≤f′(1)≤2.

答案　D

5．(2009·全国Ⅰ理，9)已知直线y＝x+1与曲线y＝ln(x+a)相切，则a的值为(　)

A．1 　　　　　　　　　　　 　B．2 　　　　　　　　　　　　 　C．－1　　　　　　　　　　　 　 D．－2

解析　设直线y＝x+1与曲线y＝ln(x+a)的切点为(x₀，y₀)，则y₀＝1+x₀，y₀＝ln(x₀+a)，

又y′＝，

∴y′＝＝1，即x₀+a＝1.又y₀＝ln(x₀+a)，

∴y₀＝0，∴x₀＝－1，∴a＝2.

答案　B

4．(2010·聊城模拟)曲线y＝e^x在点(2，e²)处的切线与坐标轴所围三角形的面积为(　)

A.e²　 　　　　　　　　　　　　　 B．2e² 　　　　　　　　　　　　　　 C．e²　 　　　　　　　　　　　 D.

解析　∵点(2，e²)在曲线上，

∴切线的斜率k＝y′|_x＝2＝e^x|_x＝2＝e²，

∴切线的方程为y－e²＝e²(x－2)．即e²x－y－e²＝0.

与两坐标轴的交点坐标为(0，－e²)，(1,0)，

∴S_△＝×1×e²＝.

答案　D

3．(2009·潮州一模)若曲线y＝x⁴的一条切线l与直线x+4y－8＝0垂直，则l的方程为(　)

A．4x－y－3＝0　 　　　　　　　　　　　　　　　　　　　　　　 B．x+4y－5＝0

C．4x－y+3＝0　 　　　　　　　　　　　　　　　　　　　　　　　 D．x+4y+3＝0

解析　y′＝4x³＝4，得x＝1，即切点为(1,1)，所以过该点的切线方程为y－1＝4(x－1)，

整理得4x－y－3＝0.

答案　A

2．(2009·临沂模拟)若点P是曲线y＝x²－ln x上任意一点，则点P到直线y＝x－2的最小距

离为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．1　 　　　　　　　　　　　　　 B. 　　　　　　　　　　　　　 　C. 　　　　　　　　　　　　 　D.

解析　过点P作y＝x－2的平行直线，且与曲线y＝x²－ln x相切，设P(x₀，x－ln x₀)，则k＝y′|x＝x₀＝2x₀－，

∴2x₀－＝1，∴x₀＝1或x₀＝－(舍去)．

∴P(1,1)，∴d＝＝.

答案　B

1．(2010·佛山模拟)一质点沿直线运动，如果由始点起经过t秒后的位移为s＝t³－t²+2t，

那么速度为零的时刻是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．0秒　 　　　　　　　　　　　　　　　　　　　　　　 B．1秒末

C．2秒末　 　　　　　　　　　　　　　　　　　　　　 D．1秒末和2秒末

解析　∵s＝t³－t²+2t，

∴v＝s′(t)＝t²－3t+2，令v＝0，得t₁＝1，t₂＝2.

答案　D

12．(14分)(2009·金华模拟)在海岸A处，发现北偏东45°方向，距离A(－1)n mile的B处

有一艘走私船，在A处北偏西75°的方向，距离A 2 n mile的C处的缉私船奉命以10 n

mile/h的速度追截走私船．此时，走私船正以10 n mile/h的速度从B处向北偏东30°方向

逃窜，问缉私船沿什么方向能最快追上走私船？

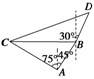解　如图所示，注意到最快追上走私船且两船所用时间相等，

若在D处相遇，则可先在△ABC中求出BC，再在△BCD中求

∠BCD.

设缉私船用t h在D处追上走私船，

则有CD=10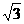t，BD=10t.

在△ABC中，∵AB=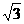-1，AC=2，

∠BAC=120°，

∴由余弦定理，

得BC²=AB²+AC²-2AB·AC·cos∠BAC

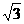=(-1)²+2²-2×(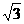-1)×2×cos 120°=6，

∴BC=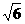，∵∠CBD=90°+30°=120°，

在△BCD中，由正弦定理，得

sin∠BCD=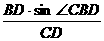

=，

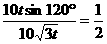∴∠BCD=30°.

即缉私船沿北偏东60°方向能最快追上走私船．

11．(13分)(2009·鲁东南三地四市联合考试)在△ABC中，已知cos A＝.

(1)求sin²－cos(B+C)的值；

(2)若△ABC的面积为4，AB＝2，求BC的长．

解　(1)sin²－cos(B+C)＝+cos A

＝+＝.

(2)在△ABC中，∵cos A＝，∴sin A＝.

由S_△ABC＝4，得bcsin A＝4，得bc＝10.

∵c＝AB＝2，∴b＝5.

∴BC²＝a²＝b²+c²－2bccos A

＝5²+2²－2×5×2×＝17.∴BC＝.