
题目列表(包括答案和解析)
4.(2010·广州模拟)设f(x)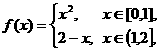 则,
则,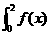 dx等于 ( )
dx等于 ( )
A.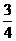 B.
B.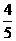 C.
C. D.不存在,
D.不存在,
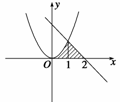 解析 本题应画图求解,更为清晰,如图,
解析 本题应画图求解,更为清晰,如图,
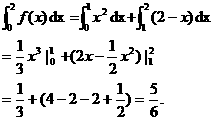
答案 C
3.(2010·洛阳质检)若ʃ(2x-3x2)dx=0,则k等于 ( )
A.0 B.1
C.0或1 D.以上均不对
解析 ʃ(2x-3x2)dx=ʃ2xdx-ʃ3x2dx
=x2|-x3|=k2-k3=0,∴k=0或k=1.
答案 C
2.(2009·潍坊模拟)若函数f(a)=ʃ(2+sin x)dx,则f等于 ( )
A.1 B.0
C.2π+3+cos 1 D.1-cos 1
解析 ∵f(a)=ʃ(2+sin x)dx
=(2x-cos x)|=2a-cos a+1,
∴f=π+1,
∴f=f(π+1)=2(π+1)-cos(π+1)+1
=2π+cos 1+3.
答案 C
1.(2010·德州阶段检测)ʃ-(sin x+cos x)dx的值是 ( )
A.0 B. C.2 D.4
解析 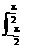 (sin
x+cos
x)dx
(sin
x+cos
x)dx
=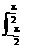 sin
xdx+
sin
xdx+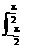 cos
xdx
cos
xdx
=(-cos x)|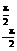 |+sin x|
|+sin x|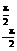
=-cos +cos+sin -sin
=1-(-1)=2.
答案 C
12.(14分)(2009·四川文,20)已知函数f(x)=x3+2bx2+cx-2的图象在与x轴交点处的切线
方程是y=5x-10.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+mx,若g(x)的极值存在,求实数m的取值范围以及函数g(x)取得极
值时对应的自变量x的值.
解 (1)由已知,得切点为(2,0),故有f(2)=0,
即4b+c+3=0,①
f′(x)=3x2+4bx+c,由已知,得f′(2)=12+8b+c=5.
即8b+c+7=0.②
联立①、②,解得b=-1,c=1,
于是函数解析式为f(x)=x3-2x2+x-2.
(2)g(x)=f(x)+mx=x3-2x2+x-2+mx,
g′(x)=3x2-4x+1+,令g′(x)=0.
当函数有极值时,Δ≥0,方程3x2-4x+1+=0有实根,
由Δ=4(1-m)≥0,得m≤1.
①当m=1时,g′(x)=0有实根x=,在x=左右两侧均有g′(x)>0,故函数g(x)无极值.
②当m<1时,g′(x)=0有两个实根,
x1=(2-),x2=(2+),
当x变化时,g′(x)、g(x)的变化情况如下表:
|
x |
(-∞,x1) |
x1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
g′(x) |
+ |
0 |
- |
0 |
+ |
|
g(x) |
? |
极大值 |
? |
极小值 |
? |
故在m∈(-∞,1)时,函数g(x)有极值:
当x=(2-)时,g(x)有极大值;
当x=(2+)时,g(x)有极小值.
§3.3 定积分

11.(13分)(2010·南阳一模)已知a是实数,函数f(x)=x2(x-a),
(1)若f′(1)=3,求a的值及曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)在区间[0,2]上的最大值.
解 (1)f′(x)=3x2-2ax,因为f′(1)=3-2a=3,
所以a=0.又当a=0时,f(1)=1,f′(1)=3,
所以曲线y=f(x)在点(1,f(1))处的切线方程为
3x-y-2=0.
(2)令f′(x)=0,解得x1=0,x2=,
当≤0,即a≤0时,f(x)在[0,2]上单调递增,
从而f(x)max=f(2)=8-4a;
当≥2时,即a≥3时,f(x)在[0,2]上单调递减,
从而f(x)max=f(0)=0;
当0<<2,即0<a<3,f(x)在上单调递减,在上单调递增.
从而f(x)max=
综上所述,f(x)max=
10.(13分)(2010·开封调研)已知向量a=(x2,x+1),b=(1-x,t).若函数f(x)=a·b在区间(-
1,1)上是增函数,求t的取值范围.
解 f(x)=a·b=x2(1-x)+t(x+1)
=-x3+x2+tx+t,
∴f′(x)=-3x2+2x+t.
∵f(x)在(-1,1)上是增函数,
∴-3x2+2x+t≥0在x∈(-1,1)上恒成立.
∴t≥3x2-2x,令g(x)=3x2-2x,x∈(-1,1).
∴g(x)∈,∴t≥5.
9.(2009·合肥调研)函数f(x)=x3+3ax2+3[(a+2)x+1]有极大值又有极小值,则a的取值范围是________.
解析 ∵f(x)=x3+3ax2+3[(a+2)x+1],
∴f′(x)=3x2+6ax+3(a+2).
令3x2+6ax+3(a+2)=0,即x2+2ax+a+2=0.
∵函数f(x)有极大值和极小值,
∴方程x2+2ax+a+2=0有两个不相等的实根.
即Δ=4a2-4a-8>0,∴a>2或a<-1.
答案 a>2或a<-1
8.(2009·湖州一模)已知函数f(x)=-x3+ax在区间(-1,1)上是增函数,则实数a的取值范围
是________.
解析 由题意应有f′(x)=-3x2+a≥0,在区间(-1,1)上恒成立,则a≥3x2,x∈(-1,1)
恒成立,故a≥3.
答案 a≥3
7.(2009·江苏,3)函数f(x)=x3-15x2-33x+6的单调减区间为________.
解析 ∵f′(x)=3x2-30x-33=3(x-11)(x+1),令f′(x)<0得-1<x<11,∴函数f(x)=x3
-15x2-33x+6的单调减区间为(-1,11).
答案 (-1,11)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com