2．(2010·济宁联考)若a>2，则函数f(x)＝x³－ax²+1在区间(0,2)上恰好有(　)

A．0个零点　 　　　　　　　　　　　　　　　　　　　　　　 B．1个零点

C．2个零点　 　　　　　　　　　　　　　　　　　　　　　　 D．3个零点

解析　解答本题要结合二分法和函数的单调性判断．由已知得：f′(x)＝x(x－2a)，由于a>2，故当0<x<2时f′(x)<0，即函数为区间(0,2)上的单调递减函数，又当a>2时f(0)f(2)＝－4a<0，故据二分法及单调性可知函数在区间(0,2)上有且只有一个零点．

答案　B

1．(2010·广州调研)若函数f(x)＝x³－3x+a有3个不同的零点，则实数a的取值范围是(　)

A．(－2,2)　 　　　　　　　　　　　　　　　　　　　　　　　 B．[－2,2]

C．(－∞，－1)　 　　　　　　　　　　　　　　　　　　　 D．(1，+∞)

解析　本题考查了函数零点的判断方法及一元二次方程根与系数的关系．由于函数f(x)是

连续的，故只需两个极值异号即可．f′(x)＝3x²－3，令3x²－3＝0，则x＝±1，只需

f(－1)·f(1)<0，即(a+2)(a－2)<0，故a∈(－2,2)．

答案　A

12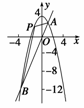．(14分)(2009·台州模拟)如图所示，抛物线y=4-x²与直线y=3x的两

交点为A、B，点P在抛物线上从A向B运动．

(1)求使△PAB的面积最大的P点的坐标(a，b)；

(2)证明由抛物线与线段AB围成的图形，被直线x＝a分为面积相等

的两部分．

(1)解　解方程组，得x₁＝1，x₂＝－4.

∴抛物线y＝4－x²与直线y＝3x的交点为

A(1,3)，B(－4，－12)，

∴P点的横坐标a∈(－4,1)．

点P(a，b)到直线y＝3x的距离为d＝，

∵P点在抛物线上，∴b＝4－a²，

d′_a＝·(4－3a－a²)′＝(－2a－3)＝0，

∴a＝－，即当a＝－时，d最大，

这时b＝4－＝，

∴P点的坐标为时，△PAB的面积最大．

(2)证明　设上述抛物线与直线所围成图形的面积为S，

位于x＝－右侧的面积为S₁.

S＝ʃ(4－x²－3x)dx＝，

S₁＝ʃ¹－(4－x²－3x)dx＝，

∴S＝2S₁，即直线x＝－平分抛物线与线段AB围成的图形的面积．

§3.4　导数的综合应用

11．(13分)(2010·龙岩阶段测试)已知f(x)为二次函数，且f(－1)＝2，f′(0)＝0，

ʃf(x)dx＝－2.

(1)求f(x)的解析式；

(2)求f(x)在[－1,1]上的最大值与最小值．

解　(1)设f(x)＝ax²+bx+c (a≠0)，

则f′(x)＝2ax+b.

由f(－1)＝2，f′(0)＝0，

得，即.∴f(x)＝ax²+(2－a)．

又ʃf(x)dx＝ʃ[ax²+(2－a)]dx

＝|＝2－a＝－2.

∴a＝6，∴c＝－4.从而f(x)＝6x²－4.

(2)∵f(x)＝6x²－4，x∈[－1,1]，

所以当x＝0时，f(x)_min＝－4；当x＝±1时，f(x)_max＝2.

10．(13分)(2010·汉沽调研)计算下列定积分

(1)ʃdx；

(2)ʃ²dx；

(3)ʃ₀(sin x－sin 2x)dx.

解　(1)ʃdx＝|

＝－ln 2－＝－ln 2.

(2)ʃ²dx＝ʃdx

＝|

＝－(2+ln 2+4)

＝ln +.

(3)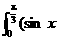－sin 2x)dx＝|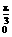

＝－＝－.

9．(2008·山东理，14)设函数f(x)＝ax²+c　 (a≠0)，若

ʃf(x)dx＝f(x₀),0≤x₀≤1，则x₀的值为________．

解析　ʃ(ax²+c)dx＝ax+c，∴＝ax，

∵a≠0，∴x＝，又0≤x₀≤1，∴x₀＝.

答案　

8．(2009·广东三校一模)ʃ(2x^k+1)dx＝2，则k＝________.

解析　ʃ(2x^k+1)dx＝|

＝+1＝2，＝1，∴k＝1.

答案　1

7．(2009·福建改编)ʃ－(1+cos x)dx＝________.

解析　∵(x+sin x)′＝1+cos x，

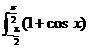∴dx＝(x+sin x)|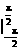

＝+sin－＝π+2.

答案　π+2

6．(2010·佛山一模)一物体在变力F(x)＝5－x²(力单位：N，位移单位：m)作用下，沿与F(x)

成30°方向作直线运动，则由x＝1运动到x＝2时F(x)作的功为　　　　　　　　　　　　　 (　)

A. J　 　　　　　　　　 B. J　 　　　　　　　　　 C. J　 　　　　　　　　　 D．2 J

解析　由于F(x)与位移方向成30°角．如图：F在位移方向上的分力F′＝F·cos 30°，

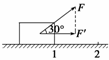W＝ʃ(5－x²)·cos 30°dx＝ʃ(5－x²)dx

＝|＝×＝ (J)．

答案　C

5.(2009·烟台模拟)曲线y＝cos x(0≤x≤)与坐标轴围成的面积是　　　　　 (　)

A．4　 　　　　　　　　　　 B. 　　　 　　　　　　　 　C．3 　　　　　　　　 　D．2

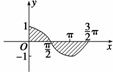解析　先作出y＝cos x的图象，如图所示，从图象中

可以看出

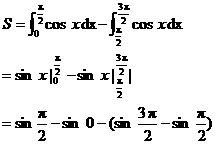
=1-0-(-1-1)=3.

答案　C