4．(2009·温州模拟)定义运算：a*b＝，

如1]　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．R　 　　　　　　　　　　　　　　　　　　　　　　　　 B．(0，+∞)

C．(0,1]　 　　　　　　　　　　　　　　　　　　　　　 D．[1，+∞)

解析　f(x)＝2^x*2^－x＝，∴f(x)在(－∞，0]上是增函数，在(0，+∞)上是减函数，∴0<f(x)≤1.

答案　 C

3．(2010·菏泽联考)已知函数y＝4^x－3×2^x+3，当其值域为[1,7]时，x的取值范围是(　)

A．[2,4]　 　　　　　　　　　　　　　　　　　　　　　 B．(－∞，0]

C．(0,1]∪[2,4] 　　　　　　　　　　　　　　　　　　　　　 D．(－∞，0]∪[1,2]

解析　y＝(2^x)²－3×2^x+3＝²+∈[1,7]，

∴²∈.

∴2^x－∈∪.

∴2^x∈[－1,1]∪[2,4]，∴x∈(－∞，0]∪[1,2]．

答案　D

2．(2009·新乡模拟)函数f(x)=ax-b的图象如右图，其中a、b为常数，则下

列结论正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．a>1，b<0

B．a>1，b>0

C．0<a<1，b>0

D．0<a<1，b<0

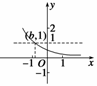解析　由图象得函数是减函数，

∴0<a<1.

又分析得，图象是由y=ax的图象向左平移所得，

∴-b>0，即b<0.从而D正确．

答案　D

1．(2010·滨州一模)下列等式＝2a；＝；－3＝中一定成立的有　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．0个　 　　　　　　　　 B．1个　 　　　　　　　　　　 C．2个　 　　　　　　　　　　 D．3个

解析　＝a≠2a；＝－<0，

＝＝>0，∴≠；

－3<0，>0，∴－3≠.

答案　A

12．(14分)(2010·舟山调研)已知函数f(x)＝x²+ (x≠0，常数a∈R)．

(1)讨论函数f(x)的奇偶性，并说明理由；

(2)若函数f(x)在[2，+∞)上为增函数，求实数a的取值范围．

解　(1)当a＝0时，f(x)＝x²对任意

x∈(－∞，0)∪(0，+∞)，

有f(－x)＝(－x)²＝x²＝f(x)，∴f(x)为偶函数．

当a≠0时，f(x)＝x²+(x≠0，常数a∈R)，

若x＝±1，则f(－1)+f(1)＝2≠0；

∴f(－1)≠－f(1)，f(－1)≠f(1)．

∴函数f(x)既不是奇函数也不是偶函数．

综上所述，当a＝0时，f(x)为偶函数；

当a≠0时，f(x)为非奇非偶函数．

(2)设2≤x₁<x₂，

f(x₁)－f(x₂)＝x+－x－

＝[x₁x₂(x₁+x₂)－a]，

要使函数f(x)在x∈[2，+∞)上为增函数，

必须f(x₁)－f(x₂)<0恒成立．

∵x₁－x₂<0，x₁x₂>4，

即a<x₁x₂(x₁+x₂)恒成立．

又∵x₁+x₂>4，∴x₁x₂(x₁+x₂)>16，

∴a的取值范围是(－∞，16]．

§2.4　指数与指数函数

11．(13分)(2010·湖州联考)已知f(x)是R上的奇函数，且当x∈(－∞，0)时，f(x)＝－xlg(2－x)，求f(x)的解析式．

解　∵f(x)是奇函数，可得f(0)＝－f(0)，∴f(0)＝0.

当x>0时，－x<0，由已知f(－x)＝xlg(2+x)，

∴－f(x)＝xlg(2+x)，即f(x)＝－xlg(2+x) (x>0)．

∴f(x)＝

即f(x)＝－xlg(2+|x|) (x∈R)．

10．(13分)(2010·杭州模拟)设函数f(x)＝x²－2|x|－1 (－3≤x≤3)，

(1)证明f(x)是偶函数；

(2)画出这个函数的图象；

(3)指出函数f(x)的单调区间，并说明在各个单调区间上f(x)是增函数还是减函数；

(4)求函数的值域．

(1)证明　∵x∈[－3,3]，∴f(x)的定义域关于原点对称．

f(－x)＝(－x)²－2|－x|－1

＝x²－2|x|－1＝f(x)，

即f(－x)＝f(x)，∴f(x)是偶函数．

(2)解　当x≥0时，f(x)＝x²－2x－1＝(x－1)²－2，

当x<0时，f(x)=x²+2x-1

=(x+1)²-2，

即f(x)=

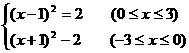
根据二次函数的作图方法，可得函数图象如图．

(3)解　函数f(x)的单调区间为

[-3，-1)，[-1,0)，[0,1)，[1,3]．

f(x)在区间[-3，-1)和[0,1)上为减函数，

在[-1,0)，[1,3]上为增函数．

(4)解　当x≥0时，函数f(x)=(x-1)2-2的最小值为-2，最大值为f(3)=2；

当x<0时，函数f(x)=(x+1)2-2的最小值为-2，最大值为f(-3)=2.故函数f(x)的值域为[-2,2]．

9．(2009·山东理，16)已知定义在R上的奇函数f(x)满足f(x－4)＝－f(x)，且在区间[0,2]上是

增函数，若方程f(x)＝m(m>0)，在区间[－8,8]上有四个不同的根x₁，x₂，x₃，x₄，则x₁+x₂+x₃+x₄＝________.

解析　因为定义在R上的奇函数，满足f(x－4)＝－f(x)，所以f(4－x)＝f(x)．因此，函数图象关于直线x＝2对称且f(0)＝0，由f(x－4)＝－f(x)知f(x－8)＝f(x)．又因为f(x)在区间[0,2]上是增函数，所以f(x)在区间[－2,0]上也是增函数，如图所示，那么方程f(x)＝m(m>0)在区间[－8,8]上有四个不同的根x₁，x₂，x₃，x₄，不妨设x₁<x₂<x₃<x₄.由对称性知x₁+x₂＝－12，x₃+x₄＝4，所以x₁+x₂+x₃+x₄＝－12+4＝－8.

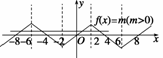
答案　－8

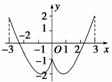
8．(2010·温州一模)设奇函数f(x)的定义域为[－5,5]，当x∈[0，5]时，函数y＝f(x)的图象如图所示，则使函数值y<0的x的取值集合为________．

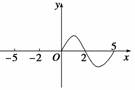
解析　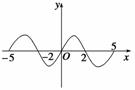由原函数是奇函数，所以y=f(x)在[-5,5]上的图象

关于坐标原点对称，由y=f(x)在[0,5]上的图象，得它在[-5,0]

上的图象，如图所示．由图象知，使函数值y<0的x的取值

集合为(-2,0)∪(2,5)．

答案　(-2,0)∪(2,5)

7．(2010·福州模拟)已知函数y＝f(x)为奇函数，若f(3)－f(2)＝1，则f(－2)－f(－3)＝______.

解析　∵f(x)为奇函数且f(3)－f(2)＝1，

∴f(－2)－f(－3)＝f(3)－f(2)＝1.

答案　1