8．(2009·池州模拟)若函数f(x)＝x²+ax+b的两个零点是－2和3，则不等式af(－2x)>0的解

集是__________．

解析　∵f(x)＝x²+ax+b的两个零点是－2,3.

∴－2,3是方程x²+ax+b＝0的两根，

由根与系数的关系知，∴，

∴f(x)＝x²－x－6.

∵不等式af(－2x)>0，

7．(2010·淮南模拟)若函数f(x)＝x²－ax－b的两个零点是2和3，则函数g(x)＝bx²－ax－1的零点是________．

解析　由，得.

∴g(x)＝－6x²－5x－1的零点为－，－.

答案　－，－

6．(2009·怀化调研)设f(x)＝x³+bx+c (b>0) (－1≤x≤1)，且f·f<0，则方程f(x)＝0在[－1,1]内　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．可能有3个实数根　 　　　　　　　　　　　　　　 B．可能有2个实数根

C．有唯一的实数根　 　　　　　　　　　　　　　　　　 D．没有实数根

解析　∵f(x)＝x³+bx+c (b>0)，

∴f′(x)＝3x²+b>0，∴f(x)在[－1,1]上为增函数，

又∵f·f<0，

∴f(x)在内存在唯一零点．

答案　C

5．(2009·杭州质检)方程|x|(x－1)－k＝0有三个不相等的实根，则

k的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　 D.

解析　本题研究方程根的个数问题，此类问题首选的方法是图

象法即构造函数利用函数图象解题，其次是直接求出所有的根．

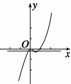
本题显然考虑第一种方法．如图，作出函数y=|x|·(x-1)的图象，

由图象知当k∈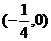时，函数y=k与y=|x|(x-1)有3个不同的交点，

即方程有3个实根．

答案　A

4．(2010·三明联考)方程|x²－2x|＝a²+1 (a∈R⁺)的解的个数是　　　　　　　　　　　　　　　　 (　)

A．1　 　　　　　　　　　　 B．2 　　　　　　　　　 C．3 　　　　　　　　　 　D．4

解析　∵a∈R+，∴a²+1>1.而y=|x²-2x|的图象如图，∴y=|x2-2x|的

图象与y=a²+1的图象总有两个交点．

∴方程有两解．

答案　B

3．(2009·福建文，11)若函数f(x)的零点与g(x)＝4^x+2x－2的零点之差的绝对值不超过0.25，

则f(x)可以是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．f(x)＝4x－1　 　　　　　　　　　　　　　　　　 B．f(x)＝(x－1)²

C．f(x)＝e^x－1　 　　　　　　　　　　　　　　　　　 D．f(x)＝ln

解析　∵g(x)＝4^x+2x－2在R上连续且g()＝+－2＝－<0，g()＝2+1－2＝1>0.

设g(x)＝4^x+2x－2的零点为x₀，则<x₀<，

0<x₀－<，∴<.

又f(x)＝4x－1零点为x＝；f(x)＝(x－1)²零点为x＝1；

f(x)＝e^x－1零点为x＝0；f(x)＝ln零点为x＝.

答案　A

2．(2009·天津理，4)设函数f(x)＝x－ln x(x>0)，则y＝f(x)　　　　　　　　　　　　　　　　　　 (　)

A．在区间，(1，e)内均有零点

B．在区间，(1，e)内均无零点

C．在区间内有零点，在区间(1，e)内无零点

D．在区间内无零点，在区间(1，e)内有零点

解析　因为f·f(1)

＝·＝>0，

因此f(x)在内无零点．

又f(1)·f(e)＝·＝<0.

因此f(x)在(1，e)内有零点．

答案　D

1．(2010·临沂模拟)设f(x)＝3^x－x²，则在下列区间中，使函数f(x)有零点的区间是(　)

A．[0,1]　 　　　　　　　　　　　　　　　　　　　　　 B．[1,2]

C．[－2，－1]　 　　　　　　　　　　　　　 　　　 D．[－1,0]

解析　∵f(－1)＝3^－1－(－1)²＝－1＝－<0，

f(0)＝3⁰－0²＝1>0，

∴f(－1)·f(0)<0，∴有零点的区间是[－1,0]．

答案　D

12．(14分)(2009·杭州学军中学第七次月考)已知函数f(x)＝x²，g(x)＝x－1.

(1)若存在x∈R使f(x)<b·g(x)，求实数b的取值范围；

(2)设F(x)＝f(x)－mg(x)+1－m－m²，且|F(x)|在[0,1]上单调递增，求实数m的取值范围．

解　(1)∃x∈R，f(x)<bg(x)⇒∃x∈R，x²－bx+b<0

⇒(－b)²－4b>0⇒b<0或b>4.

(2)F(x)＝x²－mx+1－m²，

Δ＝m²－4(1－m²)＝5m²－4.

①当Δ≤0，即－≤m≤时，则必需

⇒－≤m≤0.

②当Δ>0，即m<－或m>时，设方程F(x)＝0的根为x₁，x₂(x₁<x₂)．

若≥1，则x₁≤0，即⇒m≥2；

若≤0，则x₂≤0，即

⇒－1≤m<－；

综上所述：－1≤m≤0或m≥2.

§2.7　函数与方程

11．(13分)(2009·汕头模拟)即将开工的上海与周边城市的城际列车铁路线将大大缓解交通的

压力，加速城市之间的流通．根据测算，如果一列火车每次拖4节车厢，每天能来回16

次；如果每次拖7节车厢，则每天能来回10次，每天来回次数是每次拖挂车厢个数的一次函数，每节车厢一次能载客110人，试问每次应拖挂多少节车厢才能使每天营运人数最多？

并求出每天最多的营运人数．(注：营运人数指火车运送的人数)

解　设这列火车每天来回次数为t次，每次拖挂车厢n节，

则设t＝kn+b.由解得

∴t＝－2n+24.

设每次拖挂n节车厢每天营运人数为y，

则y＝tn×110×2＝440(－n²+12n)，

当n＝6时，总人数最多为15 840人．

答　每次应拖挂6节车厢才能使每天的营运人数最多为15 840人．