
题目列表(包括答案和解析)
2、直线:3x-4y-9=0与圆: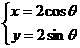 ,(θ为参数)的位置关系是( )
,(θ为参数)的位置关系是( )
A.相切 B.相离 C.直线过圆心 D.相交但直线不过圆心
1、已知点M的极坐标为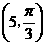 ,下列所给出的四个坐标中能表示点M的坐标是( )。
,下列所给出的四个坐标中能表示点M的坐标是( )。
A. 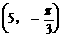 B.
B.
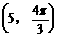 C.
C. 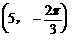 D.
D.
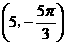
12.(14分)(2010·济宁模拟)某化工厂引进一条先进生产线生产某种化工产品,其生产的总成
本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y=-48x+8 000,已知此
生产线年产量最大为210吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最
大利润是多少?
解 (1)每吨平均成本为(万元).
则=+-48≥2 -48=32,
当且仅当=,即x=200时取等号.
∴年产量为200吨时,每吨平均成本最低为32万元.
(2)设年获得总利润为R(x)万元,
则R(x)=40x-y=40x-+48x-8 000
=-+88x-8 000
=-(x-220)2+1 680(0≤x≤210).
∵R(x)在[0,210]上是增函数,
∴x=210时,
R(x)有最大值为-(210-220)2+1 680=1 660.
∴年产量为210吨时,可获得最大利润1 660万元.
28.57-4=24.57>24,
所以,经过适当安排,老师可以在学生达到所需要的状态下讲授完这道题.
11.(13分)(2009·广东广州五校模拟)通过研究学生的学习行为,专家发现,学生的注意力随
着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的
兴趣保持较理想的状态,随后学生的注意力开始分散,设f(t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知:
f(t)=
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,教师能否在学生达到所需的状态下讲授完这道题目?
解 (1)当0<t≤10时,f(t)=-t2+24t+100
=-(t-12)2+244是增函数,且f(10)=240;
当20<t≤40时,f(t)=-7t+380是减函数,
且f(20)=240.
所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟.
(2)f(5)=195,f(25)=205,
故讲课开始25分钟时,学生的注意力比讲课开始后5分钟更集中.
(3)当0<t≤10时,f(t)=-t2+24t+100=180,则t=4;
当20<t≤40时,令f(t)=-7t+380=180,
t≈28.57,则学生注意力在180以上所持续的时间
10.(2009·重庆模拟)某旅游点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆.
为了便于结算,每辆自行车的日租金x(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(1)求函数y=f(x)的解析式及其定义域;
(2)试问当每辆自行车的日租金为多少元时,才能使一日的净收入最多?
解 (1)当x≤6时,y=50x-115,
令50x-115>0,解得x>2.3.
∵x∈N*,∴x≥3,∴3≤x≤6,x∈N*,
当x>6时,y=[50-3(x-6)]x-115.
令[50-3(x-6)]x-115>0,有3x2-68x+115<0,
上述不等式的整数解为2≤x≤20 (x∈N*),
∴6<x≤20 (x∈N*).
故y=,
定义域为{x|3≤x≤20,x∈N*}.
(2)对于y=50x-115 (3≤x≤6,x∈N*).
显然当x=6时,ymax=185(元),
对于y=-3x2+68x-115
=-32+ (6<x≤20,x∈N*).
当x=11时,ymax=270(元).
∵270>185,
∴当每辆自行车的日租金定在11元时,才能使一日的净收入最多.
9.(2010·日照一模)已知f(x)=-logcos φ(x2-ax+3a)(φ为锐角),在区间[2,+∞)上为增
函数,则实数a的取值范围是________.
答案 -4<a≤4
解析 令u=x2-ax+3a,∵0<cos φ<1,
∴y=logcos φu在定义域内为减函数,
∴f(x)=-logcos φ(x2-ax+3a)在[2,+∞)上为增函数,
则u=x2-ax+3a>0在[2,+∞)上恒成立,且为增函数,
所以,解得-4<a≤4.
8.(2009·台州质检)设函数f(x)=x|x|+bx+c,给出下列命题:
①b=0,c>0时,方程f(x)=0只有一个实数根;
②c=0时,y=f(x)是奇函数;
③方程f(x)=0至多有两个实根.
上述三个命题中所有正确命题的序号为________.
答案 ①②
解析 ①f(x)=x|x|+c=,
如图①,曲线与x轴只有一个交点,
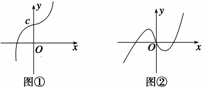
所以方程f(x)=0只有一个实数根,正确.
②c=0时,f(x)=x|x|+bx,显然是奇函数.
③当c=0,b<0时,
f(x)=x|x|+bx=.
如图②,方程f(x)=0可以有三个实数根.
综上所述,正确命题的序号为①②.
7.(2009·广州模拟)计算机的价格大约每3年下降,那么今年花8 100元买的一台计算机,9年后的价格大约是________元.
解析 设计算机价格平均每年下降p%,
由题意可得=(1-p%)3,
∴p%=1-,
∴9年后的价格y=8 1009
=8 100×3=300(元).
答案 300
6.(2009·广东六校联考)已知a>0且a≠1,f(x)=x2-ax,当x∈(-1,1)时均有f(x)<,则实数
a的取值范围是 ( )
A.∪[2,+∞) B.∪(1,4]
C.∪(1,2] D.∪[4,+∞)
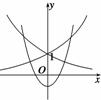
解析 由题意可知ax> 在
在
 (-1,1)上恒成立,
(-1,1)上恒成立,
令y1=ax,y2= ,
,
由图象知:
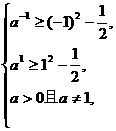
∴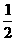 ≤a<1或1<a≤2.
≤a<1或1<a≤2.
答案 C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com