8．(2009·广东汕头二模)已知命题p：方程a²x²+ax－2＝0在[－1,1]上有解；命题q：只有一

个实数x满足不等式x²+2ax+2a≤0.若命题“p或q”是假命题，则a的取值范围是

______________________.

解析　由a²x²+ax－2＝0，得(ax+2)(ax－1)＝0，

显然a≠0，∴x＝－或x＝.

∵x∈[－1,1]，故|－|≤1或||≤1，

∴|a|≥1.

只有一个实数x满足不等式x²+2ax+2a≤0，

即抛物线y＝x²+2ax+2a与x轴只有一个交点，

∴Δ＝4a²－8a＝0，∴a＝0或a＝2.

∴命题“p或q”为真命题时，|a|≥1或a＝0.

∵命题“p或q”为假命题，

∴a的取值范围为{a|－1<a<0或0<a<1}．

答案　－1<a<0或0<a<1

7．(2010·青岛模拟)“a<0”是方程“ax²+2x+1＝0至少有一个负数根”的____________条

件．

解析　当a<0时，Δ＝4－4a>0，由韦达定理知x₁·x₂＝<0，故此一元二次方程有一个正根

和一个负根，符合题意；当ax²+2x+1＝0至少有一个负数根时，a可以为0，因为当a＝0

时，该方程仅有一根为－，所以a不一定小于0.由上述推理可知，“a<0”是方程“ax²

+2x+1＝0至少有一个负数根”的充分不必要条件．

答案　充分不必要

6．(2009·安徽改编)“a+c>b+d”是“a>b且c>d”的____________条件．

解析　由于a>b，且c>d⇒a+c>b+d，

而a+c>b+dD⇒/a>b且c>d，

所以“a+c>b+d”是“a>b且c>d”的必要不充分条件．

答案　必要不充分

5．(2010·徐州模拟)已知命题p：关于x的方程x²－ax+4＝0有实根；命题q：关于x的函数

y＝2x²+ax+4在[3，+∞)上是增函数．若p或q是真命题，p且q是假命题，则实数a的

取值范围是__________________．

解析　命题p等价于Δ＝a²－16≥0，∴a≤－4或a≥4；

命题q等价于－≤3，∴a≥－12.

p或q是真命题，p且q是假命题，则命题p和q一真一假．

∴实数a的取值范围为(－4,4)∪(－∞，－12)．

答案　(－4,4)∪(－∞，－12)

4．(2009·天津改编)设x∈R，则“x＝1”是“x³＝x”的____________条件．

解析　当x＝1时，x³＝x成立．

若x³＝x，x(x²－1)＝0，得x＝－1,0,1；不一定得到x＝1.

答案　充分不必要

3．(2009·苏州调研)命题“若a>b，则ac²>bc² (a，b∈R)”与它的逆命题、否命题、逆否命题

中，真命题的个数为________个．

解析　若a>b，c²＝0，则ac²＝bc².∴原命题为假．

若ac²>bc²，则c²≠0且c²>0，则a>b.∴逆命题为真．

又∵逆命题与否命题等价，∴否命题也为真．

又∵逆否命题与原命题等价，∴逆否命题为假．

答案　2

2．(2009·重庆改编)命题“若一个数是负数，则它的平方是正数”的逆命题是

________________．

解析　原命题的逆命题是：若一个数的平方是正数，则它是负数．

答案　若一个数的平方是正数，则它是负数

1．(2008·湖北理，2)若非空集合A、B、C满足A∪B＝C，且B不是A的子集，则下列说法

中正确的是________(填序号)．

①“x∈C”是“x∈A”的充分条件但不是必要条件

②“x∈C”是“x∈A”的必要条件但不是充分条件

③“x∈C”是“x∈A”的充要条件

④“x∈C”既不是“x∈A”的充分条件也不是“x∈A”的必要条件

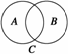解析　 由题意知，A、B、C的关系用图来表示．

若x∈C，不一定有x∈A，而x∈A，则必有x∈C，

因此“x∈C”是“x∈A”的必要条件但不是充分条件．

答案　②

12．(16分)(2010·绍兴模拟)已知{a_n}是等差数列，d为公差且不为0，a₁和d均为实数，它的

前n项和记作S_n，设集合A＝{(a_n，)|n∈N^*}，B＝{(x，y)|x²－y²＝1，x，y∈R}．试问下

列结论是否正确，如果正确，请给予证明；如果不正确，请举例说明：

(1)若以集合A中的元素作为点的坐标，则这些点都在同一条直线上；

(2)A∩B至多有一个元素；

(3)当a₁≠0时，一定有A∩B≠∅.

解　(1)在等差数列{a_n}中，对一切n∈N^*，有S_n＝，则＝＝(a₁+a_n)，

这表明点(a_n，)适合方程y＝(x+a₁)，于是点(a_n，)均在直线y＝x+a₁上．

(2)设(x，y)∈A∩B，

则x，y是方程组的解，

由方程组消去y得2a₁x+a21＝－4，

当a₁＝0时，方程2a₁x+a21＝－4无解，

此时A∩B＝∅；

当a₁≠0时，

方程2a₁x+a21＝－4只有一个解x＝，

此时，方程组只有一解，

故上述方程组至多有解，

所以A∩B至多有一个元素．

(3)取a₁＝1，d＝1，对一切的n∈N^*，

有a_n＝a₁+(n－1)d＝n>0，>0，

这时集合A中的元素作为点的坐标，其横、纵坐标均为正，

另外，由于a₁＝1≠0，如果A∩B≠∅，

那么根据(2)的结论，A∩B至多有一个元素(x₀，y₀)，而x₀＝＝－<0，y₀＝

＝－<0，这样的(x₀，y₀)∉A，产生矛盾，故a₁＝1，d＝1时，A∩B＝∅，所以，当a₁≠0时，一定有A∩B≠∅是不正确的．

§1.2　 命题及其关系、充分条件与必要条件

11．(16分)(2010·扬州模拟)设A＝{x|x²－ax+a²－19＝0}，B＝{x|x²－5x+6＝0}，C＝{x|x²+

2x－8＝0}．

(1)若A∪B＝A∩B，求实数a的值；

(2)若A∩B≠∅，且A∩C＝∅，求实数a的值；

(3)若A∩B＝A∩C≠∅，求实数a的值．

解　(1)因为A∪B＝A∩B，所以A＝B，又因为B＝{2,3}，

则a＝5且a²－19＝6同时成立，所以a＝5.

(2)因为B＝{2,3}，C＝{－4,2}，且A∩B≠∅，A∩C＝∅，则只有3∈A，即a²－3a－10＝0，

即a＝5或a＝－2，由(1)可知，当a＝5时，A＝B＝{2,3}，此时A∩C≠∅，与已知矛盾，

所以a＝5舍去，故a＝－2.

(3)因为B＝{2,3}，C＝{－4,2}，且A∩B＝A∩C≠∅，

此时只有2∈A，

即a²－2a－15＝0，得a＝5或a＝－3，

由(1)可知，当a＝5时不合题意，故a＝－3.