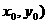4．M(为圆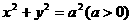内异于圆心的一点，则直线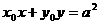与该圆的位置关系为

　　　 A．相切　　　　　　　 B．相交　　　　　　　 C．相离　　　　　　　　 D．相切或相交

3．已知两点P(4，－9)，Q(－2，3)，则直线PQ与y轴的交点分所成的比为

　　　 A．　　　　　　　　　 B．　　　　　　　　　 C．2　　　　　　　　　 D．3

2．已知两点M(－2，0)，N(2，0)，点P满足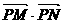＝12，则点P的轨迹方程为

　　　 A．　　　　　　　　　　　　　　　 B．x²+y²＝16

　　　 C．y²－x²＝8 　　　　　　　　　　　　　　　 D．x²+y²＝8

只有一项是符合题目要求的．

1．已知θ∈R，则直线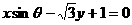的倾斜角的取值范围是

　　　 A．[0°，30°]　　　　　　　　　　　　　　　 B．[150°，180°)

　 　 C．[0°，30°]∪[150°，180°)　 　　　 D．[30°，150°]

12．(16分)(2010·镇江调研卷)已知命题p：lg(x²－2x－2)≥0，命题q：|1－|<1.若p是真命题，

q是假命题，求实数x的取值范围．

解　由lg(x²－2x－2)≥0，得x²－2x－2≥1，

∴x≥3或x≤－1；

由|1－|<1，得－1<1－<1，

∴0<x<4.

∵命题q为假，∴x≤0或x≥4.

则{x|x≥3或x≤－1}∩{x|x≤0或x≥4}

＝{x|x≤－1或x≥4}．

∴满足条件的实数x的取值范围为(－∞，－1]∪[4，+∞)．

11．(16分)(2009·江苏盐城模拟)已知命题p：“∀x∈[1,2]，x²－ln x－a≥0”与命题q：“∃

x∈R，x²+2ax－8－6a＝0”都是真命题，求实数a的取值范围．

解　∵∀x∈[1,2]，x²－ln x－a≥0，

∴a≤x²－ln x，x∈[1,2]，

令f(x)＝x²－ln x，x∈[1,2]，

则f′(x)＝x－，

∵f′(x)＝x－>0(x∈[1,2])，

∴函数f(x)在[1,2]上是增函数．

∴f(x)_min＝，∴a≤.

又由命题q是真命题得Δ＝4a²+32+24a≥0，

解得a≥－2或a≤－4.

因为命题p与q均为真命题，

所以a的取值范围为(－∞，－4]∪[－2，]．

10．(14分)(2010·徐州模拟)写出下列命题的否命题及命题的否定形式，并判断真假：

(1)若m>0，则关于x的方程x²+x－m＝0有实数根；

(2)若x、y都是奇数，则x+y是奇数；

(3)若abc＝0，则a、b、c中至少有一个为零．

解　(1)否命题：若m≤0，则关于x的方程x²+x－m＝0

无实数根，是假命题．

命题的否定：若m>0，则关于x的方程x²+x－m＝0无实数根，是假命题．

(2)否命题：若x、y不都是奇数，则x+y不是奇数，是假命题．

命题的否定：若x、y都是奇数，则x+y不是奇数，是真命题．

(3)否命题：若abc≠0，则a、b、c全不为0，是真命题．

命题的否定：若abc＝0，则a、b、c全不为0，是假命题．

9．(2009·姜堰中学高三综合练习)已知实数a满足1<a<2，命题p：函数y＝log_a(2－ax)在[0,1]

上是减函数，命题q：“|x|<1”是“x<a”的充分不必要条件，则下面说法正确的是

________．

①p或q为真命题；　②p且q为假命题；

③綈p且q为真命题；④綈p或綈q为真命题．

解析　∵1<a<2，∴y＝log_a(2－ax)在[0,1]上是减函数，即p为真．又由1<a<2，可得x<aD

⇒/|x|<1，

又|x|<1⇔－1<x<1⇒x<a，即q为真．

答案　①

8．(2010·苏州模拟)已知命题p：∀x∈[1,2]，x²－a≥0；命题q：∃x∈R，x²+2ax+2－a＝0，

若命题“p且q”是真命题，则实数a的取值范围为__________．

解析　因为“p且q”是真命题，

所以命题p、q均为真命题，

由于∀x∈[1,2]，x²－a≥0，

所以a≤1；又因为∃x∈R，x²+2ax+2－a＝0，

所以Δ＝4a²+4a－8≥0，

即(a－1)(a+2)≥0，所以a≤－2或a≥1，

综上可知，a≤－2或a＝1.

答案　a≤－2或a＝1

7．(2010·江西三校联考)设函数f(x)的定义域为R，有下列三个命题：

①若存在常数M，使得对任意x∈R，有f(x)≤M，则M是函数f(x)的最大值；

②若存在x₀∈R，使得对任意的x∈R，且x≠x₀，有f(x)<f(x₀)，则f(x₀)是函数f(x)的最大值；

③若存在x₀∈R，使得对任意的x∈R，有f(x)≤f(x₀)，则f(x₀)是函数f(x)的最大值．

这些命题中，真命题的个数是________．

解析　②③符合最大值的定义，它们是正确的，而①是错误的．

答案　2