
题目列表(包括答案和解析)
4.锅中煮有芝麻馅汤圆6个,花生馅汤圆5个,豆沙馅汤圆4个,这三种汤圆的外部特征完全相同。从中任意舀取4个汤圆,则每种汤圆都至少取到1个的概率为( )
A.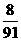 B.
B.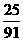 C.
C.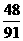 D.
D.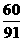
3.考察正方体6个面的中心,从中任意选3个点连成三角形,再把剩下的3个点也连成三角形,则所得的两个三角形全等的概率等于
A.1 B. 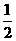 C.
C.
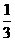 D.
0
D.
0
2.在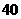 根纤维中,有
根纤维中,有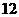 根的长度超过
根的长度超过 ,从中任取一根,取到长度超过
,从中任取一根,取到长度超过 的纤维的概率是( )
的纤维的概率是( )
A.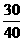 B.
B.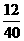 C.
C.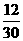 D.以上都不对
D.以上都不对
1.先后抛掷骰子三次,则至少一次正面朝上的概率是( )
A.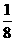 B.
B.  C.
C.
 D.
D.
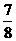
23.解 (Ⅰ)设需要新建 个桥墩,
个桥墩,
所以 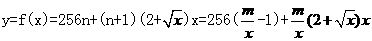
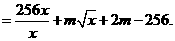
(Ⅱ) 由(Ⅰ)知,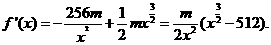
令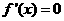 ,得
,得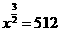 ,所以
,所以 =64
=64
当0< <64时
<64时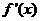 <0,
<0, 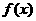 在区间(0,64)内为减函数;
在区间(0,64)内为减函数;
当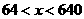 时,
时,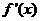 >0.
>0.
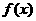 在区间(64,640)内为增函数,
在区间(64,640)内为增函数,
所以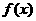 在
在 =64处取得最小值,此时,
=64处取得最小值,此时,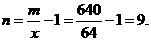
故需新建9个桥墩才能使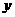 最小。
最小。
22.解:(I)由已知,切点为(2,0),故有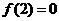 ,即
,即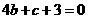 ……①
……①
又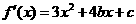 ,由已知
,由已知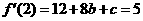 得
得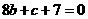 ……②
……②
联立①②,解得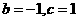 .
.
所以函数的解析式为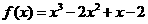 …………………………………4分
…………………………………4分
(II)因为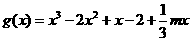
令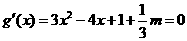
当函数有极值时,则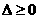 ,方程
,方程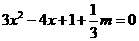 有实数解,
有实数解,
由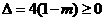 ,得
,得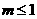 .
.
①当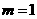 时,
时,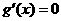 有实数
有实数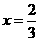 ,在
,在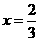 左右两侧均有
左右两侧均有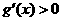 ,故函数
,故函数 无极值
无极值
②当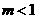 时,
时,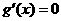 有两个实数根
有两个实数根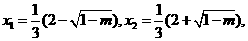
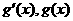 情况如下表:
情况如下表:
 |
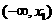 |
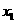 |
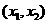 |
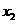 |
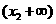 |
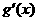 |
+ |
0 |
- |
0 |
+ |
 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以在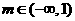 时,函数
时,函数 有极值;
有极值;
当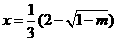 时,
时, 有极大值;当
有极大值;当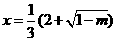 时,
时, 有极小值;
有极小值;
…………………………………12分
21.解(Ⅰ)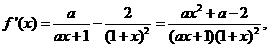
∵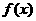 在x=1处取得极值,∴
在x=1处取得极值,∴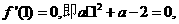 解得
解得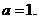
(Ⅱ)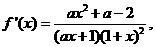
∵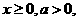 ∴
∴
①当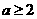 时,在区间
时,在区间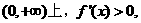 ∴
∴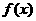 的单调增区间为
的单调增区间为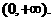
②当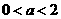 时,
时,
由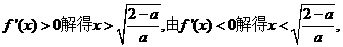
∴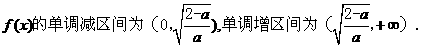
(Ⅲ)当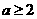 时,由(Ⅱ)①知,
时,由(Ⅱ)①知,
当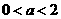 时,由(Ⅱ)②知,
时,由(Ⅱ)②知,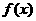 在
在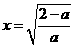 处取得最小值
处取得最小值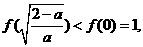
综上可知,若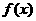 得最小值为1,则a的取值范围是
得最小值为1,则a的取值范围是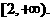
20.解:(1)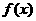 的定义域为
的定义域为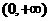 。
。
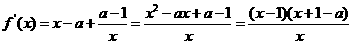 2分
2分
(i)若 即
即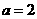 ,则
,则
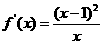
故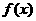 在
在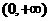 单调增加。
单调增加。
(ii)若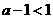 ,而
,而 ,故
,故 ,则当
,则当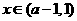 时,
时,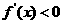 ;
;
当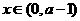 及
及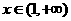 时,
时,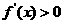
故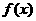 在
在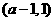 单调减少,在
单调减少,在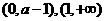 单调增加。
单调增加。
(iii)若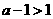 ,即
,即 ,同理可得
,同理可得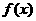 在
在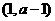 单调减少,在
单调减少,在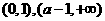 单调增加.
单调增加.
(II)考虑函数 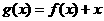
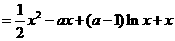
则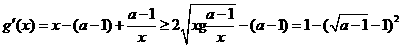
由于1<a<5,故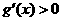 ,即g(x)在(4, +∞)单调增加,从而当
,即g(x)在(4, +∞)单调增加,从而当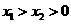 时有
时有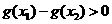 ,即
,即 ,故
,故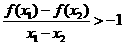 ,当
,当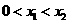 时,有
时,有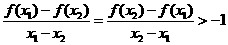 ·········12分
·········12分
19. 解法一:(1)如图,由题意知AC⊥BC,
解法一:(1)如图,由题意知AC⊥BC, ,
,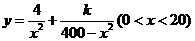
其中当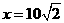 时,y=0.065,所以k=9
时,y=0.065,所以k=9
所以y表示成x的函数为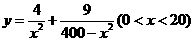
(2)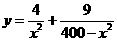 ,
,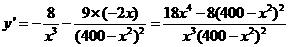 ,
,
令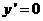 得
得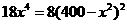 ,所以
,所以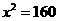 ,即
,即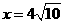 ,当
,当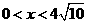 时,
时, 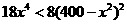 ,即
,即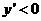 所以函数为单调减函数,当
所以函数为单调减函数,当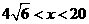 时,
时, 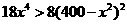 ,即
,即 所以函数为单调增函数.所以当
所以函数为单调增函数.所以当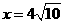 时, 即当C点到城A的距离为
时, 即当C点到城A的距离为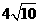 时, 函数
时, 函数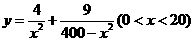 有最小值.
有最小值.
解法二: (1)同上.
(2)设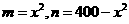 ,
,
则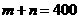 ,
,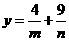 ,所以
,所以
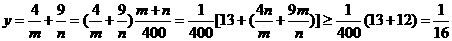 当且仅当
当且仅当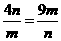 即
即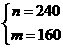 时取”=”.
时取”=”.
下面证明函数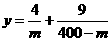 在(0,160)上为减函数, 在(160,400)上为增函数.
在(0,160)上为减函数, 在(160,400)上为增函数.
设0<m1<m2<160,则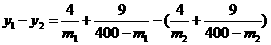

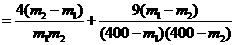
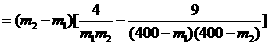
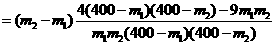 ,
,
因为0<m1<m2<160,所以4 >4×240×240
>4×240×240
9 m1m2<9×160×160所以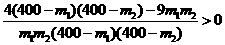 ,
,
所以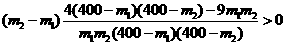 即
即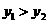 函数
函数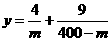 在(0,160)上为减函数.
在(0,160)上为减函数.
同理,函数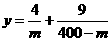 在(160,400)上为增函数,设160<m1<m2<400,则
在(160,400)上为增函数,设160<m1<m2<400,则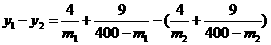
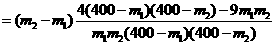
因为1600<m1<m2<400,所以4 <4×240×240, 9 m1m2>9×160×160
<4×240×240, 9 m1m2>9×160×160
所以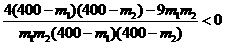 ,
,
所以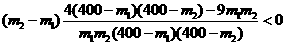 即
即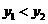 函数
函数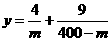 在(160,400)上为增函数.
在(160,400)上为增函数.
所以当m=160即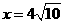 时取”=”,函数y有最小值,
时取”=”,函数y有最小值,
所以弧 上存在一点,当
上存在一点,当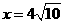 时使建在此处的垃圾处理厂对城A和城B的总影响度最小.
时使建在此处的垃圾处理厂对城A和城B的总影响度最小.
[命题立意]:本题主要考查了函数在实际问题中的应用,运用待定系数法求解函数解析式的 能力和运用换元法和基本不等式研究函数的单调性等问题.
18.解:本小题主要考查函数的概念、性质、图象及解一元二次不等式等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力。满分16分
(1)若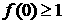 ,则
,则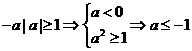
(2)当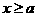 时,
时,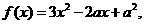
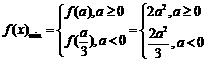
当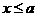 时,
时,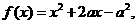
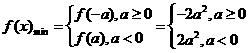
综上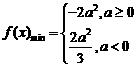
(3)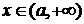 时,
时,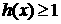 得
得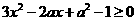 ,
,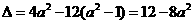
当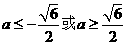 时,
时, ;
;
当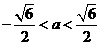 时,△>0,得:
时,△>0,得: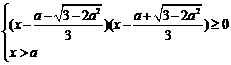
讨论得:当 时,解集为
时,解集为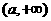 ;
;
当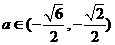 时,解集为
时,解集为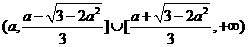 ;
;
当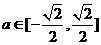 时,解集为
时,解集为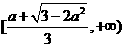 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com