
题目列表(包括答案和解析)
18. 已知:以点C (t, )(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程.
17.解 (1)

由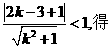
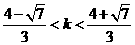 .
.
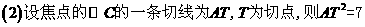
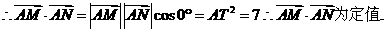
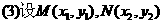
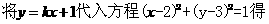
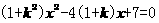
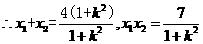
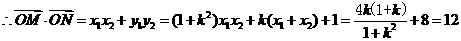
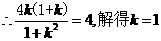
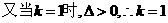 .
.
17. 已知过点A(0,1),且方向向量为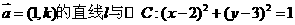 ,相交于M、N两点.
,相交于M、N两点.
(1)求实数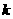 的取值范围;
的取值范围;
(2)求证: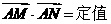 ;
;
(3)若O为坐标原点,且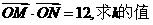 .
.


16.[答案]:4
[解析]:可得圆方程是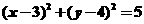 又由圆的切线性质及在三角形中运用正弦定理得
又由圆的切线性质及在三角形中运用正弦定理得
16. 过原点O作圆x2+y2‑-6x-8y+20=0的两条切线,设切点分别为P、Q,则线段PQ的长为 。
15.[答案]: 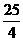
[解析]:由题意可直接求出切线方程为y-2=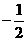 (x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和
(x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和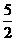 ,所以所求面积为
,所以所求面积为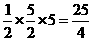 。
。
15. 已知圆O: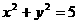 和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于
和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于
14.[答案]: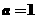
[解析]:由知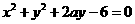 的半径为
的半径为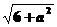 ,由图可知
,由图可知
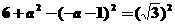 解之得
解之得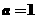
14. 若圆 与圆
与圆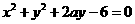 (a>0)的公共弦的长为
(a>0)的公共弦的长为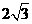 ,
,
则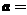 ___________ 。
___________ 。
[考点定位]本小题考查圆与圆的位置关系,基础题。
13.[答案]:4
[解析]:由题知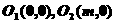 ,且
,且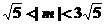 ,又
,又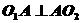 ,所以有
,所以有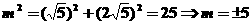 ,∴
,∴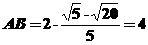 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com