
题目列表(包括答案和解析)
4、某几何体的一条棱长为 ,在该几何体的正视图中,这条棱的投影是长为
,在该几何体的正视图中,这条棱的投影是长为 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )
的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )
A. B.
B. C.
C. D.
D. 中学学科
中学学科
3.(2009全国卷Ⅱ文) 已知正四棱柱 中,
中,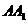 =
= ,
, 为
为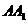 重点,则异面直线
重点,则异面直线 与
与 所形成角的余弦值为( )
所形成角的余弦值为( )
 A.
A.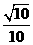 B.
B. 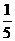 C.
C.
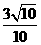 D.
D.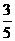
2、在△ABC中, ,若使绕直线
,若使绕直线 旋转一周,则所形成的几何体的体积是( )
旋转一周,则所形成的几何体的体积是( )
A.  B.
B. 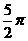 C.
C.  D.
D. 
1、(2009山东卷理)已知α,β表示两个不同的平面,m为平面α内的一条直线,则“ ”是“
”是“ ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
5. 已知:四棱柱 的三视图如下
的三视图如下
⑴ 画出此四棱柱的直观图,并求出四棱柱的体积
 ⑵ 若
⑵ 若 为
为 上一点,
上一点, 平面
平面 ,试确定
,试确定 点位置,并证明
点位置,并证明 平面
平面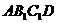
解:⑴
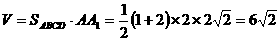
 ⑵ 作
⑵ 作 交
交 于
于 ,连
,连 ,则
,则 共面
共面 
4.(2009江西卷文)(本小题满分12分)
如图,在四棱锥 中,底面
中,底面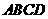 是矩形,
是矩形, 平面
平面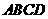 ,
,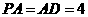 ,
, .以
.以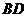 的中点
的中点 为球心、
为球心、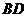 为直径的球面交
为直径的球面交 于点
于点 .
.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)求直线 与平面
与平面 所成的角;
所成的角;
 (3)求点
(3)求点 到平面
到平面 的距离.
的距离.
解:方法(一):
(1)证:依题设,M在以BD为直径的球面上,则BM⊥PD.
因为PA⊥平面ABCD,则PA⊥AB,又AB⊥AD,
所以AB⊥平面PAD,则AB⊥PD,因此有PD⊥平面ABM,所以平面ABM⊥平面PCD.
(2)设平面ABM与PC交于点N,因为AB∥CD,所以AB∥平面PCD,则AB∥MN∥CD,
由(1)知,PD⊥平面ABM,则MN是PN在平面ABM上的射影,
所以
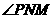 就是
就是 与平面
与平面 所成的角,
所成的角,
且


所求角为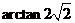
(3)因为O是BD的中点,则O点到平面ABM的距离等于D点到平面ABM距离的一半,由(1)知,PD⊥平面ABM于M,则|DM|就是D点到平面ABM距离.
因为在Rt△PAD中,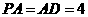 ,
, ,所以
,所以 为
为 中点,
中点,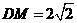 ,则O点到平面ABM的距离等于
,则O点到平面ABM的距离等于 。
。
3.(2009全国卷Ⅱ文)(本小题满分12分)
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1
(Ⅰ)证明:AB=AC
(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小
解析:本题考查线面垂直证明线面夹角的求法,第一问可取BC中点F,通过证明AF⊥平面BCC1,再证AF为BC的垂直平分线,第二问先作出线面夹角,即证四边形AFED是正方形可证平面DEF⊥平面BDC,从而找到线面夹角求解。此题两问也可建立空间直角坐标系利用向量法求解。
解法一:(Ⅰ)取BC中点F,连接EF,则EF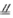
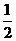
 ,从而EF
,从而EF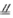 DA。
DA。


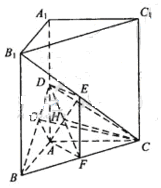
连接AF,则ADEF为平行四边形,从而AF//DE。又DE⊥平面 ,故AF⊥平面
,故AF⊥平面 ,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。
,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。
(Ⅱ)作AG⊥BD,垂足为G,连接CG。由三垂线定理知CG⊥BD,故∠AGC为二面角A-BD-C的平面角。由题设知,∠AGC=600..
设AC=2,则AG= 。又AB=2,BC=
。又AB=2,BC= ,故AF=
,故AF= 。
。
由 得2AD=
得2AD= ,解得AD=
,解得AD= 。
。
故AD=AF。又AD⊥AF,所以四边形ADEF为正方形。
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF。
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD。
连接CH,则∠ECH为 与平面BCD所成的角。
与平面BCD所成的角。
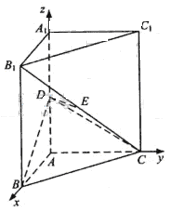 因ADEF为正方形,AD=
因ADEF为正方形,AD= ,故EH=1,又EC=
,故EH=1,又EC= =2,
=2,
所以∠ECH=300,即 与平面BCD所成的角为300.
与平面BCD所成的角为300.
解法二:
(Ⅰ)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A-xyz。
设B(1,0,0),C(0,b,0),D(0,0,c),则 (1,0,2c),E(
(1,0,2c),E(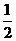 ,
, ,c).
,c).
于是 =(
=(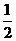 ,
, ,0),
,0),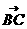 =(-1,b,0).由DE⊥平面
=(-1,b,0).由DE⊥平面 知DE⊥BC,
知DE⊥BC,  =0,求得b=1,所以 AB=AC。
=0,求得b=1,所以 AB=AC。
(Ⅱ)设平面BCD的法向量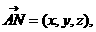 则
则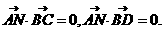 又
又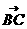 =(-1,1, 0),
=(-1,1, 0),
 =(-1,0,c),故
=(-1,0,c),故
令x=1, 则y=1, z= ,
, =(1,1,
=(1,1,
 ).
).
又平面 的法向量
的法向量 =(0,1,0)由二面角
=(0,1,0)由二面角 为60°知,
为60°知, =60°,
=60°,
故 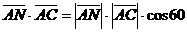 °,求得
°,求得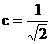
 于是
于是  ,
, 
 ,
, °
°
所以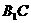 与平面
与平面 所成的角为30°
所成的角为30°
1(2009江苏卷)
如图,在直三棱柱 中,
中, 、
、 分别是
分别是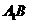 、
、 的中点,点
的中点,点 在
在 上,
上,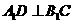 。
。
求证:(1)EF∥平面ABC;
(2)平面
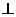 平面
平面 .
.

2.如图,在五面体 中,点
中,点 是矩形
是矩形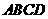 的对角线的交点,面
的对角线的交点,面 是等边三角形,棱
是等边三角形,棱 .中学高.考.资.源.网
.中学高.考.资.源.网
(1)
证明 //平面
//平面 ;
;
(2)
设 ,证明
,证明 平面
平面 .
.
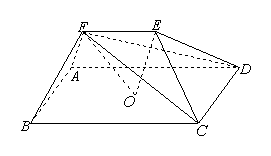
证明:(Ⅰ)取CD中点M,连结OM.在矩形ABCD中, ,又
,又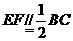 ,则
,则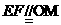 ,中学学
,中学学
连结EM,于是四边形EFOM为平行四边形.  又
又 平面CDE, EM
平面CDE, EM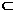 平面CDE,∴ FO∥平面CDE
平面CDE,∴ FO∥平面CDE
(Ⅱ)证明:连结FM,由(Ⅰ)和已知条件,在等边△CDE中, 且
且 .
.
因此平行四边形EFOM为菱形,从而EO⊥FM而FM∩CD=M,
∴CD⊥平面EOM,从而CD⊥EO. 而 ,所以EO⊥平面CDF. 高
,所以EO⊥平面CDF. 高
6.[答案]D
[解析]:①取前面棱的中点,证AB平行平面MNP即可;③可证AB与MP平行
5.[答案]B
[解析]:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面及为
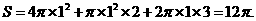 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com