
题目列表(包括答案和解析)
5、 [解析]此类求曲面上最短路程问题通常考虑侧面展开。侧面展开后得矩形 ,其中
,其中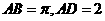 问题转化为在
问题转化为在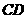 上找一点
上找一点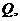 使
使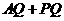 最短作
最短作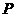 关于
关于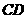 的对称点
的对称点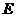 ,连接
,连接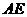 ,令
,令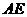 与
与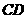 交于点
交于点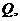 则得
则得 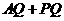 的最小值为
的最小值为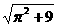
 [答案]
[答案]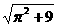
4、[解析]本题是立体几何中的最值问题,建立数学模型,用函数解决是一种重要方法。过A作AH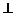 BP于H,连CH,
BP于H,连CH,
∴ .
.
 ∴
∴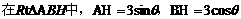 .
.
在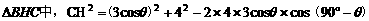 ,
,
∴在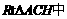 ,
,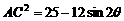 ,∴
,∴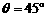 时,AC长最小;
时,AC长最小;
[答案]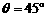
3、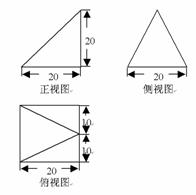 [解析] 三视图是新增考点,根据三张图的关系,可知几何体是正方体的一部分,是一个四棱锥。本题也可改编为求该几何体的外接球的表面积,则必须补全为正方体,增加了难度。
[解析] 三视图是新增考点,根据三张图的关系,可知几何体是正方体的一部分,是一个四棱锥。本题也可改编为求该几何体的外接球的表面积,则必须补全为正方体,增加了难度。
[答案]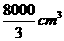
2、[答案]1),4);
[解析] 传统空间位置关系的判断依然是高考小题考查的重点,解决此类问题,可多参考教室空间,或手中的笔与桌子这些具体模型。
1、[解析]本题不告知翻折的角度,意在提醒学生找不变量。不难发现正方形对角线交点到四个顶点的距离相等,故交点即为球心,半径为1。
[答案]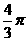
6、[答案]B
5、[答案]D
[解析]从三视图可以观察发现几何体是正三棱柱,底面边长为2cm,高为1cm,所以体积为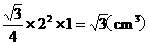 .
.
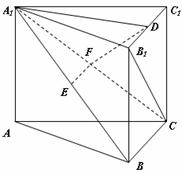
4、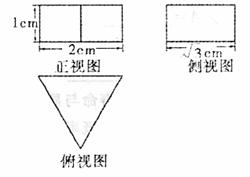 [答案]C[解析]:结合长方体的对角线在三个面的投影来理解计算。如图设长方体的高宽高分别为
[答案]C[解析]:结合长方体的对角线在三个面的投影来理解计算。如图设长方体的高宽高分别为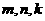 ,由题意得
,由题意得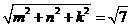 ,
, 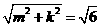
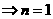
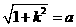 ,
,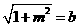 ,所以
,所以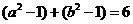
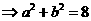 ,
,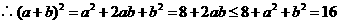
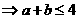 当且仅当
当且仅当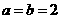 时取等号
时取等号
3.[答案]:C[解析]:本题考查异面直线夹角求法,方法一:利用平移,CD’∥BA' ,因此求△EBA'中∠A'BE即可,易知EB=
,因此求△EBA'中∠A'BE即可,易知EB=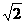 ,A'E=1,A'B=
,A'E=1,A'B=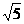 ,故由余弦定理求cos∠A'BE=
,故由余弦定理求cos∠A'BE=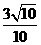 ,或由向量法可求。
,或由向量法可求。
2、[答案].A [解析]: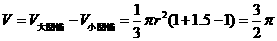
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com