
题目列表(包括答案和解析)
9. 粉碎机的下料斗是无底、无盖的正四棱台形,它的上、下底面边长分别为40cm、50cm,高是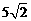 cm, 计算制造这样一个下料斗所需铁板的面积.(结果保留到1
cm, 计算制造这样一个下料斗所需铁板的面积.(结果保留到1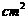 )
)
8. 柱体的体积计算公式为“底面积 高=
高=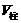 ”,将一块
”,将一块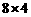 的矩形折成一个四棱柱的侧面,则卷成的棱柱的体积是 ;如折成的是正三棱柱的侧面,则体积是 .
的矩形折成一个四棱柱的侧面,则卷成的棱柱的体积是 ;如折成的是正三棱柱的侧面,则体积是 .
7. 有以下四个命题1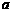 //
//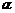 ,
,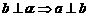 ;2
;2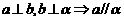 3
3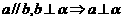 4
4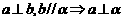 . 其中正确的命题是: .
. 其中正确的命题是: .
6. 如图所示,PA⊥平面ABC,∠ACB=90°,且PA=AC=BC=2,则:①二面角P―BC―A的大小为 ;② PB与底面ABC所成的角的正切值等于 .
5. 过三棱柱 ABC-A1B1C1 的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有( )条.
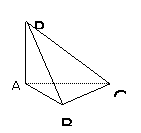 A.2 B.4 C.6 D.8
A.2 B.4 C.6 D.8
4. 平面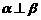 ,直线
,直线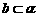 ,
,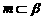 ,且
,且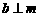 ,则
,则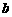 与
与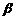 ( ).
( ).
A.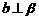 B.
B.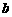 与
与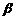 斜交 C.
斜交 C.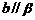 D.位置关系不确定
D.位置关系不确定
3. 一个圆锥的母线长为20cm,母线与轴的夹角为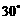 ,则圆锥的高为( )
,则圆锥的高为( )
A.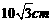 B.
B.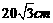 C.
C. D.
D.
2. 已知一几何体的三视图如图所示,则该几何体的体积为( )
A.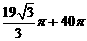 B.
B. 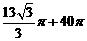
C. 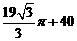 D.
D. 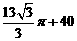
1. 下列四个命题中,正确的一个是( )
A.空间的三个点确定一个平面 B.四边形一定是平面图形
C.梯形一定是平面图形 D.六边形一定是平面图形
解法一:(1)
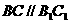 ,
,

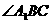 就是异面直线
就是异面直线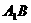 与
与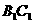 所成的角,
所成的角,
即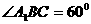 ,……(2分)
,……(2分)
连接 ,又
,又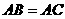 ,则
,则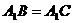

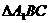 为等边三角形,……………………………4分
为等边三角形,……………………………4分
由 ,
,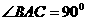
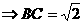 ,
,

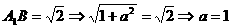 ;………6分
;………6分
(2)取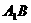 的中点
的中点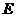 ,连接
,连接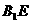 ,过
,过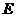 作
作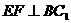 于
于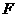 ,连接
,连接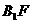 ,
,
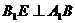 ,
,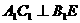
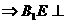 平面
平面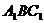
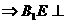
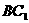 ………………8分
………………8分
又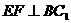 ,所以
,所以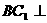 平面
平面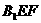 ,即
,即 ,
,
所以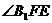 就是平面
就是平面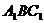 与平面
与平面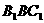 所成的锐二面角的平面角。…………10分
所成的锐二面角的平面角。…………10分
在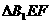 中,
中,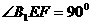 ,
,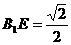 ,
,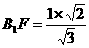 ,
,

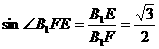
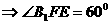 ,…………………………13分
,…………………………13分
因此平面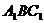 与平面
与平面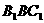 所成的锐二面角的大小为
所成的锐二面角的大小为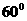 。…………14分
。…………14分
说明:取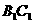 的中点
的中点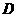 ,连接
,连接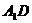 ,…………同样给分(也给10分)
,…………同样给分(也给10分)
解法二:(1)建立如图坐标系,于是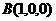 ,
,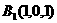 ,
,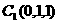 ,
,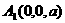 (
(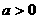 )
)
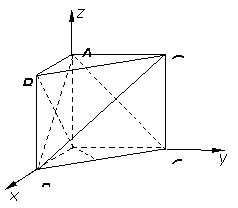
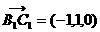 ,
,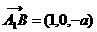 ,
,
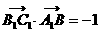 …………3分
…………3分
由于异面直线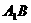 与
与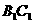 所成的角
所成的角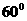 ,
,
所以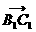 与
与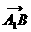 的夹角为
的夹角为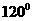
即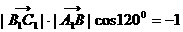
 ………6分
………6分
(2)设向量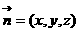 且
且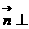 平面
平面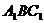
于是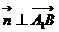 且
且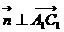 ,即
,即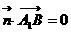 且
且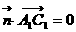 ,
,
又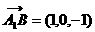 ,
,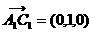 ,所以
,所以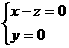 ,不妨设
,不妨设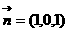 ……8分
……8分
同理得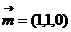 ,使
,使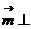 平面
平面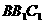 ,(10分)
,(10分)
设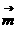 与
与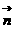 的夹角为
的夹角为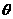 ,所以依
,所以依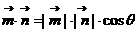 ,
,
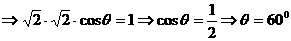 ,………………12分
,………………12分
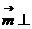 平面
平面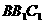 ,
,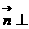 平面
平面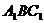 ,
,
因此平面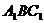 与平面
与平面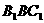 所成的锐二面角的大小为
所成的锐二面角的大小为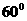 。…………14分
。…………14分
说明:或者取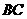 的中点
的中点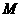 ,连接
,连接 ,于是
,于是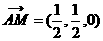 显然
显然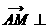 平面
平面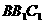
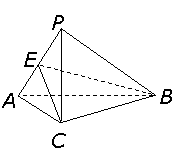
2. 解法一:(Ⅰ)取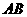 中点
中点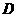 ,连结
,连结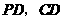 .
.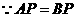 ,
,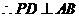 .
.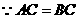 ,
,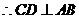 .
.
 ,
,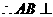 平面
平面 .
.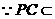 平面
平面 ,
,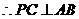 .
.
(Ⅱ)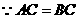 ,
,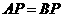 ,
,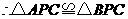 .又
.又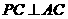 ,
,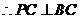 .
.
又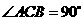 ,即
,即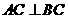 ,且
,且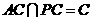 ,
,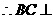 平面
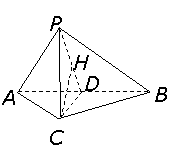
平面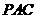 .取
.取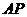 中点
中点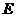 .连结
.连结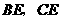 .
.
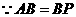 ,
,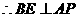 .
.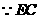 是
是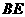 在平面
在平面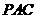 内的射影,
内的射影,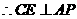 .
.
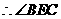 是二面角
是二面角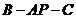 的平面角.在
的平面角.在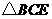 中,
中,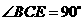 ,
,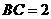 ,
,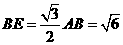 ,
, .
.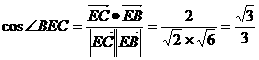 中学高.考.资.源.网
中学高.考.资.源.网
(Ⅲ)由(Ⅰ)知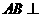 平面
平面 ,
, 平面
平面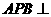 平面
平面 .过
.过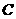 作
作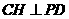 ,垂足为
,垂足为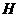 .
.
 平面
平面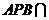 平面
平面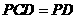 ,
,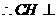 平面
平面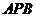 .
. 的长即为点
的长即为点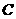 到平面
到平面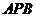 的距离.
的距离.
由(Ⅰ)知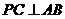 ,又
,又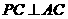 ,且
,且 ,
,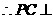 平面
平面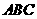 .
.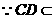 平面
平面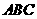 ,
,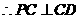 .在
.在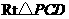 中,
中,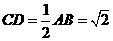 ,
,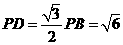 ,中学高.考.资.源.网
,中学高.考.资.源.网
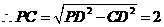 .
.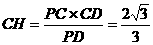 .
.
 点
点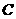 到平面
到平面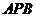 的距离为
的距离为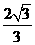 .中学学科
.中学学科
网解法二:(Ⅰ)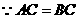 ,
,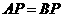 ,
,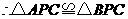 .又
.又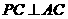 ,
,
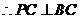 .
.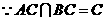 ,
,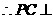 平面
平面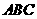 .
. 平面
平面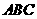 ,
,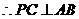 .
.
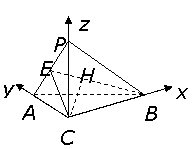
(Ⅱ)如图,以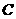 为原点建立空间直角坐标系
为原点建立空间直角坐标系 .则
.则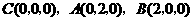 .
.
设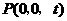 .
.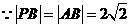 ,
,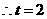 ,
,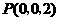 .取
.取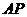 中点
中点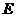 ,连结
,连结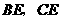 .
.
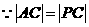 ,
,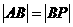 ,
,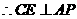 ,
,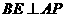 .
.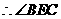 是二面角
是二面角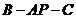 的平面角.
的平面角.
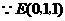 ,
,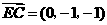 ,
,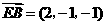 ,中学高.考.资.源.网
,中学高.考.资.源.网
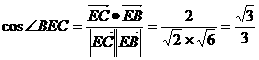 .
.
(Ⅲ)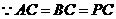 ,
,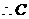 在平面
在平面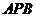 内的射影为正
内的射影为正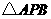 的中心
的中心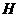 ,且
,且 的长为点
的长为点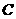 到平面
到平面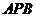 的距离.
的距离.
如(Ⅱ)建立空间直角坐标系 .
.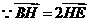 ,
, 点
点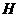 的坐标为
的坐标为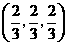 .
.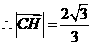 .中学学
.中学学 点
点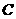 到平面
到平面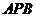 的距离为
的距离为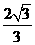 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com