22．(本小题满分14分)已知数列{a_n}中，a₁＝，点(n，2a_n+1－a_n)(n∈N^*)在直线y＝x上。

　 (I)计算a₂，a₃，a₄的值；

　 (II)令b_n＝a_n+1－a_n－1，求证：数列{b_n}是等比数列；

　 (III)设S_n、T_n分别为数列{a_n}、{b_n}的前n项和，是否存在实数λ，使得数列{}为等差数列？若存在，试求出λ的值；若不存在，请说明理由。

21．(本小题满分12分)已知定圆A：(x+1)²+y²＝16圆心为A，动圆M过点B(1,0)且和圆A相切，动圆的圆心M的轨迹记为C.

　 (I)求曲线C的方程；

　 (II)若点P(x₀,y₀)为曲线C上一点，求证：直线l: 3x₀x+4y₀y－12＝0与曲线C有且只有一个交点。

20．(本小题满分12分)已知函数。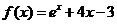

　 (Ⅰ)求证函数在区间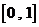上存在唯一的零点，并用二分法求函数零点的近似值(误差不超过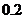)；(参考数据，，_，)；

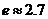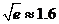　 (Ⅱ)当时，若关于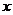的不等式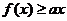恒成立，试求实数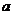的取值范围．

19．(本小题满分12分)甲、乙、丙三人进行传球练习，共传球三次，球首先从甲手中传出。

　 (Ⅰ)试列举出所有可能的传球的方法；

　 (Ⅱ)求第3次球恰好传回给甲的概率。

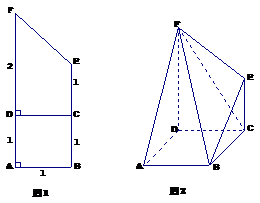
18．(本小题满分12分)如图1，在直角梯形中(图中数字表示线段的长度)，将直角梯形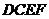沿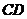折起，使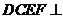平面平面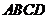，连结部分线段后围成一个空间几何体，如图2．

　 (Ⅰ)求证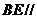：平面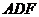；(Ⅱ)求三棱锥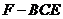的体积。.网

17．(本小题满分12分)在△ABC中，已知AB＝，BC＝2。

　 (Ⅰ)若cosB＝－，求sinC的值；

　 (Ⅱ)求角C的取值范围．

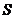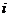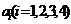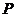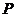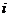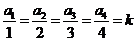16．设面积为的平面四边形的第条边的边长记为，是该四边形内任意一点，点到第条边的距离记为，若，则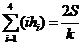．类比上述结论，体积为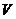的三棱锥的第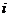个面的面积记为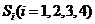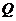，是该三棱锥内的任意一点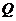，点到第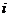个面的距离记为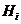，相应的正确命题是　　　　　　　　 ；

15．根据如图所示的算法流程图，可知输出的结果T为　 　　　　　；

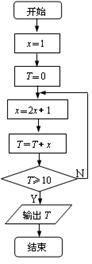
14．若函数f(x)＝x³－3bx+b在区间(0，1)内有极小值，则b应满足的条件是 　　　；

将答案填在题中的横线上。

13．若复数z＝sinα－i(1－cosα)是纯虚数，则α=　　 　　　　；