
题目列表(包括答案和解析)
82. 两个平面同时垂直于一条直线,则两个平面平行.
已知:、是两个平面,直线l⊥,l⊥,垂足分别为A、B.
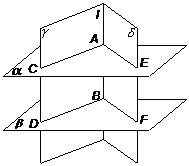 求证:∥思路1:根据判定定理证.
求证:∥思路1:根据判定定理证.
证法1:过l作平面,
∩=AC,∩=BD,
过l作平面,
∩=AE,∩=BF,
 l⊥
l⊥ l⊥AC
l⊥AC
l⊥ l⊥BD
l⊥BD
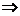 AC∥BD
AC∥BD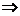 AC∥,
AC∥,
l、AC、BD共面
同理AE∥,AC∩AE≠,AC,AE ,故∥.
,故∥.
思路2:根据面面平行的定义,用反证法.
证法2:设、有公共点P
则l与P确定平面,
且∩=AP,∩=BP.
l⊥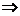 l⊥AP
l⊥AP
l⊥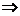 l⊥BP
l⊥BP
l、AP、BP共面,于是在同一平面内过一点有两条直线AP、BP都与l垂直,这是不可能的.
故、不能有公共点,∴ ∥.
81. 有三个几何事实(a,b表示直线,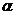 表示平面),① a∥b,② a∥
表示平面),① a∥b,② a∥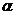 ,③ b∥
,③ b∥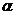 .其中,a,b在面
.其中,a,b在面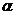 外.
外.
用其中两个事实作为条件,另一个事实作为结论,可以构造几个命题?请用文字语言叙述这些命题,并判断真伪.正确的给出证明,错误的举出反例.
解析:Ⅰ: a∥b
a∥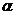
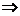 b∥
b∥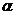
b在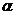 外
外
Ⅱ:a∥b
b∥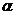
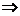 a∥
a∥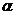
a在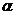 外
外
Ⅰ、Ⅱ是同一个命题:两条平行直线都在一个平面外,若其中一条与平面平行,则另一条也与该平面平行.
证明:过a作平面 与
与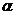 交于
交于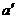
∵ a∥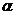
∵ a∥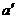
而a∥b
∴ b∥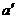 且b在
且b在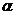 外,
外,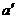 在
在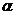 内
内
∴ b∥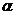 .
.
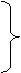 Ⅲ:a∥
Ⅲ:a∥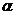
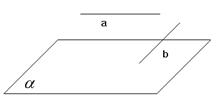
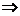 a∥b
a∥b
b∥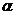
命题:平行于同一个平面的两条直线平行,
这是错的,如右图
14.已知椭圆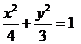 ,试确定
,试确定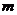 的值,使得在此椭圆上存在不同两点关于直线
的值,使得在此椭圆上存在不同两点关于直线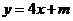 对称。
对称。
13.已知椭圆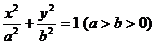 ,
,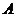 、
、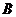 是椭圆上的两点,线段
是椭圆上的两点,线段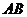 的垂直
的垂直
平分线与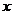 轴相交于点
轴相交于点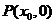 .证明:
.证明: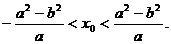
12.已知椭圆的焦点是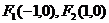 ,P为椭圆上一点,且
,P为椭圆上一点,且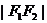 是
是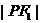 和
和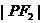 的等差中项.(1)求椭圆的方程;(2)若点P在第三象限,且∠
的等差中项.(1)求椭圆的方程;(2)若点P在第三象限,且∠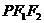 =120°,求
=120°,求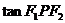 .
.
11.椭圆 的焦点
的焦点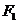 、
、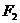 ,点
,点 为其上的动点,当∠
为其上的动点,当∠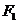

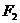 为钝角时,点
为钝角时,点 横坐标的取值范围是
。
横坐标的取值范围是
。
10.设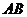 是椭圆
是椭圆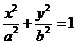 的不垂直于对称轴的弦,
的不垂直于对称轴的弦,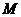 为
为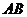 的中点,
的中点,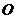 为坐标原点,
为坐标原点,
则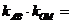 ____________。
____________。
9.椭圆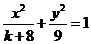 的离心率为
的离心率为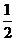 ,则
,则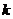 的值为______________。
的值为______________。
8.椭圆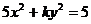 的一个焦点是
的一个焦点是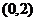 ,那么
,那么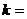 。
。
7.若椭圆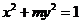 的离心率为
的离心率为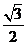 ,则它的长半轴长为_______________.
,则它的长半轴长为_______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com