7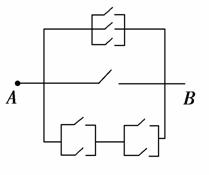．如右图所示为一电路图，若只闭合一条线路，从A到B共有______条不同的线路可通电．

解析：∵按上、中、下三条线路可分为三类，上线路中有3种，中线路中有一种，下线路中有2×2＝4(种)．根据分类计数原理，共有3+1+4＝8(种)．

答案：8

6．在1,2,3,4,5这五个数字所组成的允许有重复数字的三位数中，其各个数字之和为9的三位数共有(　)

A．16个　 　　　　　　　　B．18个

C．19个　 　　　　　　　　D．21个

解析：选C.若取三个完全不同的数字为1,3,5或2,3,4.其中每种可排3×2×1＝6(个)数．

若取有两个相同的数字，为1,4,4或2,2,5.每种可排3个数．

若取三个相同的数字，为3,3,3，可排一个数，所以共可排6×2+3×2+1＝19(个)数．

5．三边长均为正整数，且最大边长为11的三角形的个数为(　)

A．25　 　　　　　　　　　　B．26

C．36　 　　　　　　　　　　D．37

解析：选C.另两边长用x，y表示，且不妨设1≤x≤y≤11，要构成三角形，必须x+y≥12.

当y取值11时，x＝1,2,3，…，11，可有11个三角形；当y取值10时，x＝2,3，…，10，可有9个三角形；…当y取值6时，x只能取6，只有一个三角形．

∴所求三角形的个数为11+9+7+5+3+1＝36.

4．从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a，b，组成复数a+bi，其中虚数有(　)

A．36个　 　　　　　　　　　　B．42个

C．30个　 　　　　　　　　　　D．35个

解析：选A.由于a，b互不相等且为虚数，所有b只能从{1,2,3,4,5,6}中选一个有6种，a从剩余的6个选一个有6种，根据分步计数原理知虚数有6×6＝36(个)．

3．已知I＝{1,2,3}，A、B是集合I的两个非空子集，且A中所有数的和大于B中所有数的和，则集合A、B共有(　)

A．12对　 　　　　　　　　　　B．15对

C．18对　 　　　　　　　　　　D．20对

解析：选D.依题意，当A、B均有一个元素时，有3对；当B有一个元素，A有两个元素时，有8对；当B有一个元素，A有三个元素时，有3对；当B有两个元素，A有三个元素时，有3对；当A、B均有两个元素时，有3对．共20对，故选D.

2．从长度分别为1,2,3,4的四条线段中任取三条的不同取法共有n种．在这些取法中，以取出的三条线段为边可组成的三角形的个数为m，则＝(　)

A．0 　　　　　　　　　　　　　B.

C.　 　　　　　　　　　　　　　D.

解析：选B.n＝4，在“1,2,3,4”这四条线段中，由三角形的性质“两边之和大于第三边，两边之差小于第三边”知可组成三角形的有“2,3,4”，即m＝1，所以＝.

1．某城市的电话号码，由六位升为七位(首位数字均不为零)，则该城市可增加的电话部数是(　)

A．9×8×7×6×5×4×3　 　　　　B．8×9⁶

C．9×10⁶　 　　　　　　　　　　　D．81×10⁵

解析：选D.电话号码是六位数字时，该城市可安装电话9×10⁵部，同理升为七位时为9×10⁶.∴可增加的电话部数是9×10⁶－9×10⁵＝81×10⁵.

6．某体育彩票规定，从01到36共36个号中抽出的7个号为一注，每注2元．某人想先选定吉利号18，然后从01至17中选3个连续的号，从19至29中选2个连续的号，从30至36中选1个号组成一注．若这个人要把符合这种要求的号全买下，至少要花多少元钱？

解：第1步：从01到17中选3个连续号有15种选法；

第2步：从19到29中选2个连续号有10种选法；

第3步：从30到36中选1个号有7种选法．

由分步乘法计数原理可知：满足要求的注数共有15×10×7＝1050注，故至少要花1050×2＝2100元．

练习

5．从班委会5名成员中选出3名，分别担任班级学习委员、文娱委员与体育委员，其中甲、乙二人不能担任文娱委员，则不同的选法共有________种．(用数字作答)

解析：可分两步解决．

第一步，先选出文娱委员，因为甲、乙不能担任，所以从剩下的3人中选1人当文娱委员，有3种选法．

第二步，从剩下的4人中选学习委员和体育委员，又可分两步进行：第一步，先选学习委员有4种选法，第二步选体育委员有3种选法．

由分步乘法计数原理可得，不同的选法共有3×4×3＝36(种)．

答案：36

4．若x、y∈N^*，且x+y≤6，则有序自然数对(x，y)共有________个．

解析：当x＝1,2,3,4,5时，y值依次有5,4,3,2,1个，由分类计数原理，不同的数对(x，y)共有5+4+3+2+1＝15(个)．

答案：15