5．(原创题)若x>y，a>b，则在①a－x>b－y，②a+x>b+y，③ax>by，④x－b>y－a这四个式子中，恒成立的不等式的序号是________．

解析：令x＝－2，y＝－3，a＝3，b＝2，

符合题设条件x>y，a>b.

∵a－x＝3－(－2)＝5，b－y＝2－(－3)＝5，

∴a－x＝b－y，因此①不成立．

又∵ax＝－6，by＝－6，∴ax＝by，

∴③也不正确．

由不等式的性质可推出②④成立．

答案：②④

4．某地规定本地最低生活保障金不低于300元，上述不等关系写成不等式为________．

解析：设最低生活保障金为x元，则x≥300.

答案：x≥300

3．(2009年高考安徽卷)“a+c>b+d”是“a>b且c>d”的(　)

A．必要不充分条件　 　　B．充分不必要条件

C．充分必要条件　 　　　D．既不充分也不必要条件

答案：A

2．设α∈(0，)，β∈[0，]，那么2α－的取值范围是(　)

A．(0，) 　　　　　　　　B．(－，)

C．(0，π) 　　　　　　　　D．(－，π)

解析：选D.由题设得0<2α<π，0≤≤，

∴－≤－≤0，

∴－<2α－<π.

1．下列命题正确的是(　)

A．若a²>b²，则a>b　　B．若>，则a<b

C．若ac>bc，则a>b 　　　D．若<，则a<b

解析：选D.考虑a、b为负值或一正一负的情况，对于选项C，还要考虑c取正、负值的两种情况，选项A、B、C均有不成立的情况．

12．用n种不同颜色为下侧两块广告牌着色(如图甲、乙所示)，要求在①、②、③、④四个区域中相邻(有公共边界)的区域不用同一种颜色．

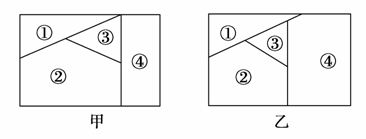
(1)若n＝6，为甲着色时共有多少种不同方法？

(2)若为乙着色时共有120种不同方法，求n.

解：完成着色这件事，共分四个步骤，可依次考虑为①、②、③、④着色时各自的方法数，再由分步计数原理确定总的着色方法数，因此：

(1)为①着色有6种方法，为②着色有5种方法，为③着色有4种方法，为④着色也只有4种方法．

∴共有着色方法6×5×4×4＝480种．

(2)与(1)的区别在于与④相邻的区域由两块变成了三块，同理，不同的着色方法数是n(n－1)(n－2)(n－3)．

由n(n－1)(n－2)(n－3)＝120，

∴(n²－3n)(n²－3n+2)－120＝0，

即(n²－3n)²+2(n²－3n)－12×10＝0，

∴n²－3n－10＝0，

∴n＝5.

11．有0、1、2、…、8这9个数字．用五张卡片，正反两面分别写上0、8；1、7；2、5；3、4；6、6；且6可作9用．这五张卡片共能拼成多少个不同的四位数？

解：由于正反两面可用，且一张卡片在拼一个四位数的过程中至多出现在一个数位上，同时首位不可为0,6可作9用，∴首位有9种拼法，百位有8种拼法，十位有6种拼法，个位有4种拼法．

∴共能拼成9×8×6×4＝1728(个)不同的四位数．

10．某单位职工义务献血，在体检合格的人中，O型血的共有28人，A型血的共有7人，B型血的共有9人，AB型血的共有3人．

(1)从中任选1人去献血，有多少种不同的选法？

(2)从四种血型的人中各选1人去献血，有多少种不同的选法？

解：从O型血的人中选1人有28种不同的选法，从A型血中选1人有7种不同的选法，从B型血的人中选1人有9种不同的选法，从AB型血的人中选1人有3种不同的选法．

(1)任选1人去献血，即无论选哪种血型的哪一个人，这件“任选1人去献血”的事情都可以完成，所以用分类计数原理．有28+7+9+3＝47种不同选法．

(2)要从四种血型的人中各选1人，即要在每种血型的人中依次选出1人后，这种“各选1人去献血”的事情才完成，所以用分步计数原理．

有28×7×9×3＝5292种不同选法．

9．从－1,0,1,2这四个数中选三个不同的数作为函数f(x)＝ax²+bx+c的系数，可组成不同的二次函数共有________个，其中不同的偶函数共有________个．(用数字作答)

解析：一个二次函数对应着a，b，c(a≠0)的一组取值，a的取法有3种，b的取法有3种，c的取法有2种，由分步乘法计数原理，知共有二次函数3×3×2＝18(个)．若二次函数为偶函数，则b＝0.同上共有3×2＝6(个)．

答案：18　6

8.山东省某中学，为了满足新课改的需要，要开设9门课程供学生选修，其中A、B、C三门由于上课时间相同，至多选一门，学校规定，每位同学选修4门，共有________种不同的选修方案．(用数值作答)

解析：第一类，若从A、B、C三门选一门有C₃¹·C₆³＝60(种)，

第二类，若从其他六门中选4门有C₆⁴＝15(种)，

∴共有60+15＝75种不同的方法．

答案：75